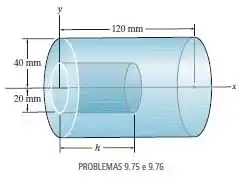
Determine a profundidade do furo no cilindro de modo que o centro de massa do sólido esteja
localizado em . O material tem densidade de .
Passo 1
E aí, pessoal!
Nesse problema temos um cilindro de raio e comprimento com um furo em sua base de raio e altura .
A partir daí temos que determinar o comprimento do furo para que o centro de massa do objeto esteja em .
Parece complicado?
Para resolver esse problema temos que aplicar a fórmulinha dos somatórios
Sendo que como o objeto é homogêneo, temos que:
Bora lá!
Passo 2
As dimensões do cilindro são fixas, então para ele temos que:
A massa do cilindro sem o furo é:
OBS: lembrando que .
Agora para o furo, temos que:
Escrevendo a fórmulinha do somatório, considerando o furo como um volume negativo...
Substituindo os valores...
Nosso objetivo é calcular de forma que , ou seja:
Com isso, chegamos em
E fim! Entendeu tudo? Responde Aí!