Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 92
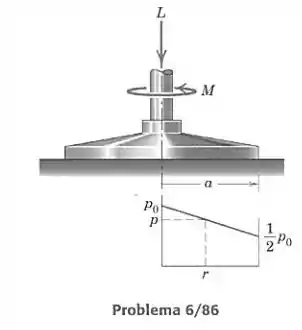
Para o disco de lixamento plano de raio , a pressão desenvolvida entre o disco e a superfície lixada decresce linearmente com , desde um valor no centro aé com . Se o coeficiente de atrito é , obtenha a expressão para o torque necessário para girar o eixo sob uma força axial .
Passo 1
Para cada ponto de área , raio e angulação , como mostrado na figura, é feita no disco pela superfície lixada uma força de atrito :
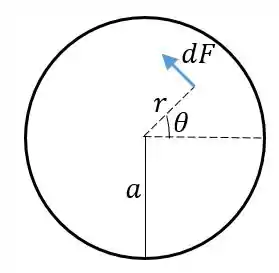
Essa pequena força infinitesimal de atrito é igual à força normal aplicada vezes o coeficiente de atrito . Mas sabemos que a força normal é a pressão vezes a área:
A área infinitesimal pode ser considerada como um comprimento vezes uma largura dada por um pequeno arco , então:
Finalmente, devemos calcular o momento infinitesimal que cada força de atrito causa em torno do centro:
Devemos então para obter o momento total integrar essa expressão, com variando de a e variando de a .
Passo 2
Então temos que calcular a integral dupla:
A parte da esquerda é calculada diretamente:
A expressão de em função de é uma reta decrescente com . Vamos calcular então a expressão de :
Então calculamos a integral:
Passo 3
Temos o momento total, mas precisamos do valor de em função da força aplicada. A força total será igual a:
Já calculamos que e que , então:
Então calculamos a integral:
Então temos em função de :
Substituindo então na fórmula de :