Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 23

A extremidade A de uma haste delgada e uniforme de comprimento L e peso W é mantida em equilíbrio na superfície como mostrado na figura, enquanto a extremidade B é suportada por uma corda BC. Sabendo que os coeficientes de atrito são e , determine o maior valor de para qual o movimento é iminente, o valor correspondente da tensão na corda.

Passo 1

Beleza! Vamos começar esse excercício desenhando o DCL para a haste:

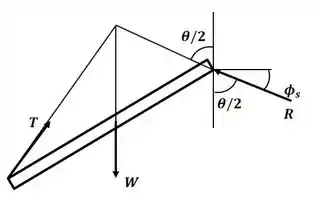
Como sabemos que o coeficiente de atrito pode ser escrito como:

Substituindo o valor dado de :

Passo 2

Agora, olhando para o DCL e para a figura do enunciado, podemos ver que, como o segmento BA e AC possuem o mesmo comprimento L, e o peso age exatamente no meio da barra, a linha de ação da força R divide o ângulo em duas partes iguais, sendo assim, olhando para os ângulos formados com relação a força R, podemos escrever a relação:

Passo 3

Agora para encontrar o valor da tensão na corda, precisamos desenhar o triângulo de forças para o sistema:

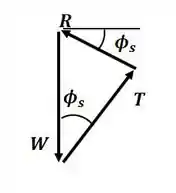
Dessa forma, por trigonometria, temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a menor força na alavanca P necessária para impedir que a roda gire se ela estiver sujeito a um torque de M = 250N ⋅ m . O coeficiente de atrito estático entre a correia e a roda é μ s = 0,3

Determine a força desenvolvida na mola A B a fim de evitar que a roda gira quando estiver sujeita a um momento de binário M = 200N ⋅ m . O coeficiente de atrito estático entre a correia e a borda da r

A polia de transmissão B em um gravador de fita de vídeo se encontra na iminência do deslizamente quando está sujeito a um torque M = 0,005N ⋅ m . Se o coeficiente de atrito estático entre a fita e a

Se a corda der três voltas completas mais a volta básica ( 165 ° ) em torno do pino, determine se o homem de 80k g pode evitar que a caixa de 300k g se mova. Os coeficientes de atrito estático entre a

A viga uniforme de 25k g está apoiada pela corda que está à ponta da viga, passa pelo pino rugoso e depois é conectada ao bloco de 50k g . Se o coeficiente de atrito estático entre a viga e o bloco e