O ioiô possui uma massa e um raio de giração em relação ao seu centro . O cordão tem um comprimento máximo e se enrola em torno do pequeno núclo central de raio com sua extremidade fixada a um ponto do núcleo. Se o ioiô é liberado a partir da posição com uma velocidade descendente de seu centro , determine a tração no cordão e a aceleração de seu centro durante os seus movimentos de subida e de descida. Encontre também a velocidade máxima de descida do seu centro.

Passo 1
Seguindo a ordem das figuras do enunciado, vamos começar analisando o movimento de descida. Precisamos de um diagrama que mostre as forças que agem sobre o ioiô:
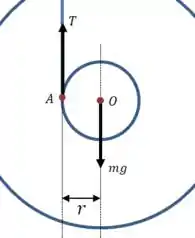
Como não conhecemos a força , vamos começar escrevendo uma equação de momentos em relação ao ponto . Dessa forma a força terá momento nulo:
E a única força que produz momento em torno do ponto será o peso:
O momento de inércia em relação ao ponto pode ser calculado usando o teorema dos eixos paralelos:
Onde é a distância entre os pontos e , e o momento pode ser calculado em função do raio de giração que foi dado no enunciado:
Então:
E já podemos isolar a aceleração angular do ioiô durante a descida:
E com isso podemos escrever a aceleração do centro de massa:
Passo 2
Agora vamos usar a segunda lei de Newton na direção vertical para tentar encontrar a força :
E a aceleração do centro de massa na direção vertical é exatamente a aceleração que acabamos de calcular:
E já podemos isolar :
Vamos simplificar um pouco essa expressão:
Passo 3
Além disso, com a aceleração, podemos calcular a velocidade máxima atingida pelo ioiô:
Claramente a velocidade será máxima quando for máximo. Nesse caso, o máximo equivale a :
Beleza, já achamos tudo o que foi pedido, mas ainda precisamos verificar o que acontece na subida.
Passo 4
O que muda no diagrama? É só dar uma olhada no desenho do enunciado:
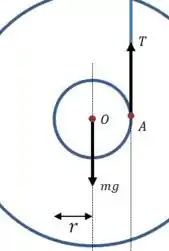
O momento da força peso agora terá o sinal oposto, mas a aceleração angular também, ou seja, ficamos com a mesma equação de antes:
A segunda lei de Newton também fica exatamente igual:
Como estaremos usando as mesmas equações, o resultado necessariamente será o mesmo.
Obs.: Faz sentido que isso seja dessa forma, assim como as equações para o movimento de um objeto lançado na vertical também são as mesmas na subida e na descida.
Resposta
A aceleração é , a tração é e a velocidade máxima é .