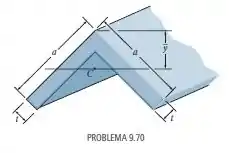
Localize o centroide para a seção transversal da viga em ângulo.
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Nesse problema temos uma viga em ângulo e nosso objetivo é encontrar o centroide em da sua área de seção transversal.
Tem ideia de como fazemos isso?
Para resolver esse problema podemos separar a área em diferentes partes e aplicar a fórmula:
Bora começar!
Passo 2
Vamos começar separando a área da seguinte maneira:
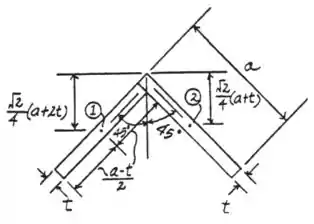
Dessa forma, temos que para a área 1, temos:
Já para a área 2, temos:
Assim, substituindo na fórmula de ...
É isso! Entendeu tudo? Responde Aí!