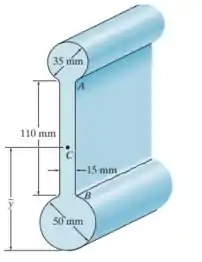
Determine a localização do centroide da seção transversal da viga. Para o cálculo, desconsidere o tamanho das soldas nos cantos em A e B.
Passo 1
Oi, tudo bem? Vamos resolver este exercício.
Nesse problema temos que encontrar a localização da coordenada do centroide da área de seção transversal da viga dada.
Lembra como fazemos isso?
A coordenada do centroide de uma área é dada por:
Bora começar!
Passo 2
Podemos separar a área da seção transversal em três regiões:
- Área 1: Circunferência de de diâmetro.
- Área 2: Retângulo .
- Área 3: Circunferência de de diâmetro.
Dessa forma, temos que para a área 1:
Para a área 2:
E para a área 3:
Tranquilo até aqui?
Passo 3
Agora é só substituir tudo em ...
E fim! O que achou? Responde Aí!