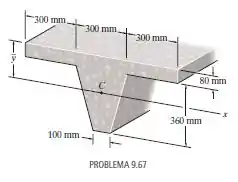
Localize o centroide da viga de concreto com a seção transversal afunilada mostrada na figura.
Passo 1
Oi, tudo bem? Vamos resolver este exercício.
Nesse problema temos que encontrar a coordenada do centro geométrico da seção transversal da viga dada no enunciado.
Lembra como fazemos isso?
A coordenada do centro geometrico de uma área pode ser calculada como:
Nesse caso podemos separar a seção em áreas e calcular por esse somatório.
Saca só!
Passo 2
Nesse problema podemos separar a seção da viga em duas regiões:
- Área 1: Retângulo de dimensão .
- Área 2: Trapézio de base maior , altura e base menor .
Dessa forma, para a área 1, temos:
Para a área 2:
Substituindo em que vimos no passo 1:
É isso! Entendeu tudo? Responde Aí!