Em um mecanismo projetado para converter movimento linear em movimente angular, o cilindro hidráulico fornece ao pino uma velocidade constante para baixo durante um curto intervalo de movimento. Determine a aceleração angular das hastes ranhuradas em termos de .
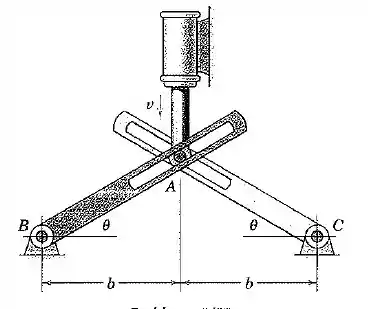
Passo 1
Para resolver esse tipo de problema é muito importante pensar em termos de geometria, porque a física em si é muito mais complicada.
Então vamos imaginar um triângulo naquele desenho:
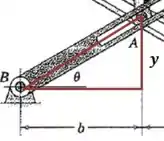
E agora podemos aproveitar aquele ângulo para escrever a seguinte relação:
E agora vamos derivar isso em relação ao tempo, sabendo que a derivada da coordenada é o negativo da velocidade que foi dada no enunciado:
E nosso objetivo é encontrar , que é a aceleração angular das hastes.
Passo 2
Vamos derivar mais uma vez:
Como é uma constante, sua derivada em relação ao tempo é nula, e para o lado direito precisamos usar a regra do produto:
Lembrando que, pela regra da cadeia:
E agora podemos isolar para encontrar :
Passo 3
Agora vamos aproveitar a relação que achamos no passo para substituir :
E agora substituímos isso na fórmula de cima:
E lembrando que :
Pronto!
Resposta
A aceleração angular das hastes é .