Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 31
A placa semicircular de espessura uniforme possui uma massa de é levantada a partir do repouso pelo mecanismo de hastes paralelas de peso desprezível sob a ação de um momento de aplicado à extremidade da haste. Calcule as componentes normal e tangencial a do cortante suportado pelo pino em logo apóso o omento ser aplicado.
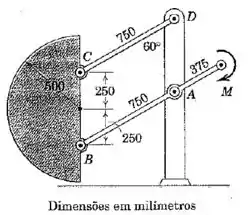
Passo 1
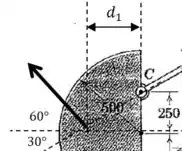
Vamos começar representando no desenho as direções tangencial e normal:
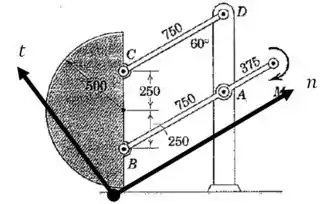
E nosso objetivo é calcular as duas componentes e da força em .
Vamos começar olhando apenas para a haste . Quando a placa está prestes a perder o contato com o chão, o momento total sobre a haste é nulo:
Isso vale para qualquer ponto de referência, mas vamos usar o ponto , para que possamos calcular a componente na outra ponta.
Em relação a , temos o momento da componente tangencial e o momento que foi dado no enunciado, atuando em sentidos opostos:
E agora podemos aplicar a segunda lei de Newton sobre a haste na direção tangencial. As únicas forças que agem nessa direção são e , então:
Da mesma forma, podemos aplicar essa equação sobre a direção normal para encontrar que:
Vamos precisar dessa relação mais tarde.
Passo 2
Agora vamos olhar para a placa. Precisamos calcular sua aceleração na direção tangencial. As únicas forças que atuam sobre a placa nessa direção são e uma componente da força peso:
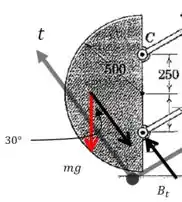
Passo 3
E se aplicarmos uma equação de momentos sobre a placa, poderemos calcular , que é igual ao que queremos calcular:
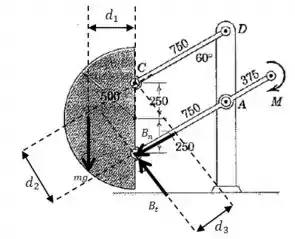
Olhando para o desenho, podemos ver o segunite:
E pode ser calculado consultando uma tabela para a posição do centro de massa de uma placa semicircular:
Então podemos calcular os momentos de todas essas forças em relação ao ponto :
Passo 4
E essa soma de momentos deve ser igual ao momento da força resultante agindo no centro de massa.
O módulo da força é:
E podemos calcular componentes dessa força nas direções vertical e horizontal, e então fica fácil calcular o momento:
E então:
E como vimos antes:
Resposta
As componentes são e .