Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 90
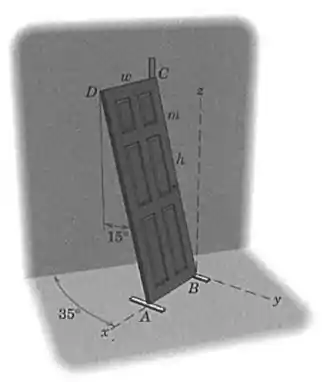
Uma porta homogênea de massa , altura e largura está encostada em uma parede para ser pintada. Pequenas ripas de madeira estão colocadas sob as quinas e . O atrito em é desprezível, mas em e é suficiente para impedir que a porta deslize. Determine as componentes e das forças de reação em e e a força normal à parede em .
Passo 1
Vamos começar enumerando as forças que estão envolvidas nessa questão. Além do peso no centro da porta, em cada um dos apoios e nós temos as componentes , , , , e , e só nos interessa calcular as componentes em e .
Já no ponto nós temos uma força normal à parede, que tem componentes e , queremos calcular as duas.
Como nós conhecemos o ângulo que a porta forma com a parede, já podemos escrever expressões para as duas componentes da normal:
E a partir daqui precisamos montar equações de equilíbrio que resolvam o problema.
Passo 2
Se tomarmos o eixo como referência, todas as forças em e terão momento nulo, e a componente da normal também! Só ficaremos com o peso no centro da porta e a componente da normal.
A distância perpendicular do ponto de aplicação da força peso até o eixo é:
E a distância perpendicular do ponto de aplicação da componente é:
Agora sim, vamos calcular o momento:
E com isso podemos calcular :
E com isso podemos calcular a normal :
E esse é nosso primeiro resultado.
Passo 3
Agora vamos escolher outros eixos que nos deem resultados úteis. Quando calculamos o momento em relação ao eixo nós excluímos todas as forças em , e as componentes e (cujas linhas de ação cruzam o eixo) e (que é paralela ao eixo).
A força peso também é paralela ao eixo, e por isso tem momento nulo. Ficamos então apenas com e :
Como já podemos calcular essa equação pode ser resolvida para encontrar :
Então:
Agora seguimos a mesma lógica para o momento em relação ao eixo . Nesse caso só vão restar as forças , e :
Passo 4
Beleza, conseguimos esses dois resultados usando o sistema de coordenadas do enunciado, em que a origem está sobre o ponto . Agora vamos usar um sistema em que a origem está sobre o ponto , e então fazer as mesmas contas.
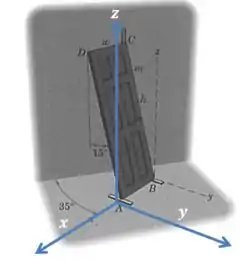
Pronto, agora vamos calcular de novo os momentos em relação ao eixo e ao eixo :
Dessa vez todas as forças em se anulam, além do peso e das componentes e :
E agora vamos olhar para o momento em relação ao novo eixo . Nesse caso as forças em também se anulam, além de , e :
Agora sim, encontramos tudo o que procurávamos.
Resposta
A força normal em é , e as componentes das forças em e são , , e .