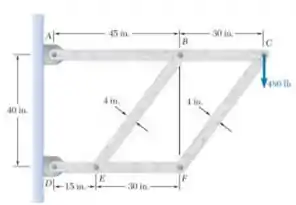
O quadro mostrado consiste em quatro elementos de madeira, ABC, DEF, BE e CF. Sabendo que cada elemento tem seção transversal retangular de 2 x 4-in e que cada pino tem um diâmetro de 1/2 in., determine o valor médio máximo da tensão normal (a) no elemento BE, (b) no elemento CF
Passo 1
E ai gurizada tudo belezinha??? Antes de exercitarmos que tal esboçarmos um diagrama de corpo livre para melhor visualização?
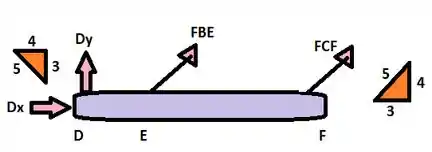
Agora vamos calcular o somatório do momento :D
Vamos calcular novamente o somatório do momento em F
E por último e não menos importante calcularmos o momento em E :D
Passo 2
- Antes de encontrarmos a tensão precisamos calcular a área na seção BE , venha comigo
- Assim como no passo 2, precisamos calcular a área para seção CF :D
Agora sim podemos encontrar a tensão
Passo 3
Agora sim podemos encontrar a tensão