Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 75
Resolver o Prob. 10.74, assumindo que as barras e são substituídas por cabos de aço de de diâmetro.
Passo 1
Fala, galerinha! Partiu fazer uma questão de carregamentos produzidos por impacto?
Essa questão quer que a gente determine a deformação máxima que ocorre no centro da barra . A deformação máxima é a deformação causada pelo impacto do bloco , quando ele transfere toda a sua energia potencial para a barra. Ou seja, a barra absorve toda a energia potencial, se deformando por isso. A figura abaixo mostra esse caso!
são as forças que os suportes e exercem sobre a barra . é a força que o bloco que cai exerce sobre a barra . é a deformação dos suportes e causada pelo choque que a barra sofre. é o diâmetro e e o comprimento dos suportes e .
Para achar a deflexão de , temos que calcular a energia potencial que absorve.
onde é a massa do bloco. Vemos pela equação acima que, além de , temos outros dois termos que não conhecemos: e . Ou seja, para calcular , precisamos saber quanto valem a deformação dos suportes e a energia que total absorvida pelos suportes e pela barra em função de . Desse jeito, a equação acima terá apenas como incógnita e poderemos achar esse valor. Vamos começar achando em função de no passo seguinte!
Passo 2
A primeira etapa para achar a deformação dos suportes e , que são carregados com uma força , é usar a Lei de Hooke abaixo.
onde é a área da seção transversal de um dos suportes.
No entanto, ainda não conhecemos a força que estica os suportes. Para encontrar essa força, temos que fazer o equilíbrio de forças da barra . Esse equilíbrio de forças diz que a soma das forças aplicadas em tem que ser zero.
O sinal de é negativo, porque essa força aponta pra baixo!
Nós queremos achar em função de , no entanto, esbarramos de novo em uma variável que não conhecemos: . Para achar em função de recorremos à equação presente no apêndice para o tipo de carregamento encontrado na barra .
Substituindo essa equação de na equação de :
Substituindo na equação de , achamos:
Agora só falta achar em função de !
Passo 3
Para calcular a energia total que os dois suportes e a barra absorvem, precisamos somar a energia do suporte com a energia do suporte mais a energia da barra . A energia dos suportes podem ser calculadas pela equação 10.14 do livro. Já a energia da barra é calculada resolvendo uma integral do momento fletor da barra .
Conhecemos a equação de em função de . Resta saber, como podemos transformar a integral em uma equação de . Fazemos isso, calculando o momento fletor e integrando!
Para achar precisamos usar a equação de equilíbrio de momento na parte esquerda da barra . Calcularemos o equilíbrio no ponto . O momento tem dois valores: um quando a parte esquerda da barra ainda não inclui a força e outro quando a parte esquerda inclui a força . Vamos começar o cálculo do primeiro valor de .
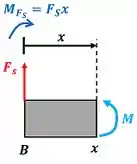
Como a força faz a barra tender a girar no sentido horário, vamos colocar um sinal de menos na frente do momento de .
Agora vamos calcular o segundo valor de .
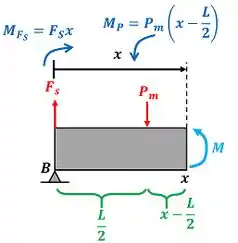
De novo precisamos observar que, como a força faz a barra tender a girar no sentido horário, vamos colocar um sinal de menos na frente do momento de .
tem dois valores. Um quando vale entre e e outro, quando vale entre e .
Por isso, para substituir na integral que calcula , precisamos separar a integral em duas. Uma que vai de a para o primeiro valor de e outra que vai de a para o segundo valor de .
Resolvendo a integral, achamos que vale:
Substituindo isso na equação de , achamos:
Aeee! Agora vamos para o passo final!
Passo 4
Finalmente podemos substituir e na equação do passo 1 e achar o valor de .
A equação acima, mostra que para achar , precisamos achar a raiz positiva do polinômio do segundo grau através da fórmula de Bhaskara. No entanto, para achar a raiz, precisamos achar os valores numéricos dos coeficientes do polinômio. Para isso, precisamos descobrir quanto vale o momento de inércia do perfil através de para perfis quadrangulares abaixo.
Além disso, vale:
Antes de substituir os dados na equação, precisamos converter de pra multiplicando por e converter , e de pra multiplicando , e por .
Pelo polinômio acima nós vemos que os coeficientes dele são:
Sabendo disso, somos capazes de calcular por Bhaskara.
Fooooooi! Depois de muuuito suor acabamos a questão! Parabéns!