Usando uma roseta de 45°, foram determinadas as deformações específicas e para um determinado ponto. Usando o círculo de Mohr, mostre que as deformações específicas principais são

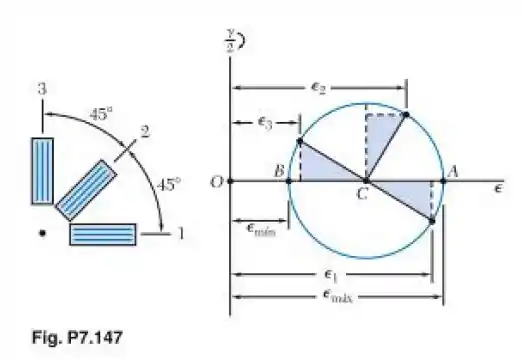
(Sugestão: Os triângulos sombreados são congruentes.)

Como vimos no passo 1, vamos precisar da deformação média. No nosso caso, como as direções 1 e 3 estão separadas por 90°, teremos:

Beleza! Agora nós vamos escrever o comprimento pro lado do triângulo, que está na horizontal, mais próximo ao ponto A da figura dada no enunciado. Podemos fazer isso utilizando a tensão média e a tensão até a extremidade desse lado, subtraindo uma da outra, temos somente o comprimento do lado, que é o que nos interessa, então teremos:

Substituindo a expressão obtida para , teremos:

Beleza, agora vamos encontrar o comprimento do outro lado do triângulo, o lado menor. Como o enunciado nos disse que os triângulos são congruentes, podemos utilizar o triângulo que está “em pé” dentro do círculo de Mohr, pegar a deformação que vai até aquele ponto e subtrair a deformação média até o centro do círculo, dessa forma, teremos:

Substituindo a expressão obtida para , teremos:

Beleza, então a hipotenusa desse triângulo será o raio do círculo de Mohr, de modo que podemos escrever:

Substituindo as expressões encontradas para e obtidas no passo 2, teremos:

Desenvolvendo essa expressão, teremos:

Podemos reescrever esses 5 termos como 2 produtos notáveis, da seguinte forma:

Opa, estamos chegando no formato do enunciado, agora tirando a raiz dos dois lados, temos:

Então, sabendo que a deformação máxima e mínima pode ser dada através de:

Substituindo as expressões encontradas para e , teremos:

Que é exatamente a equação dada no enunciado! Shoow, conseguimos mais um!