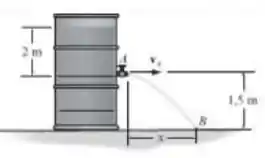
A velocidade do jato de água saindo do orifício pode ser obtida de , onde é a distância do orifício até a superfície livre da água. Determine o tempo para uma partícula de água deixando o orifício alcançar o ponto B e a distância horizontal onde ela bate na superfície.

Temos um problema de queda livre! Assumindo uma gota de água como uma partícula sólida (esta pequena hipótese torna tudo tão mais simples!), ela possui uma velocidade apenas na direção . E qual a velocidade da gota na direção ??? Zero!!! Isto mesmo, a velocidade inicial na direção é zero. Entretanto, ela está sujeita a ação da gravidade (é por isto que ela cai).

Sendo assim, para descobrirmos o tempo necessário que ela caia, basta resolvermos a equação da cinemática para a direção . Já para descobrirmos a distância até o ponto , precisamos trabalhar também com as equações da cinemática, só que na direção do eixo !

Um pequeno detalhe: vamos assumir o ponto A como a nossa origem .