Exercícios de Movimento curvilíneo - Lista de Exercícios Resolvida

Um projétil é lançado em um fluido experimental no instante . A velocidade inicial é e o ângulo com a horizontal é . O arrasto sobre o projétil resulta em um termo de aceleração , onde é a constante e é a velocidade do projétil. Determine as componentes e da velocidade e do deslocamento como funções do tempo. Qual é a velocidade final? Inclua os efeitos da aceleração gravitacional.

Uma partícula que se move em um movimento curvilíneo tem coordenadas em milímetros que variam com o tempo em segundos de acordo com e . Determine os módulos da velocidade e aceleração e os ângulos que estes vetores fazem com o eixo quando .

No instante , a velocidade de uma partícula que se desloca no plano é . No instante , a sua velocidade torna-se . Determine o módulo de sua aceleração média durante este intervalo e o ângulo dado pela aceleração média com o eixo positivo .

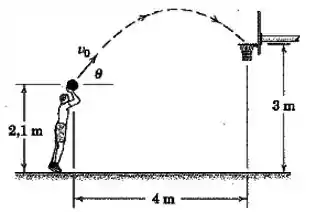
O jogador de basquete gosta de arremessar seu lance livre em um ângulo com a horizontal como mostrado. Que velocidade inicial fará com que a bola passe através do centro do aro?

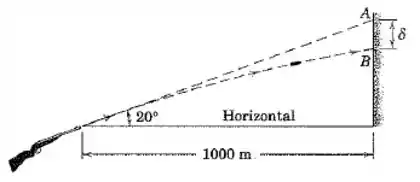
Se o cano da espingarda mostrada aponta para o ponto , calcule a distância abaixo de até o ponto onde a bala incide. A velocidade de saída no disparo da bala é de .

Uma partícula que se desloca em movimento bidimensional tem coordenadas em milímetros dadas por e , onde é o tempo em segundos. Determine os módulos da velocidade e a aceleração e o ângulo entre estes dois vetores no instante .

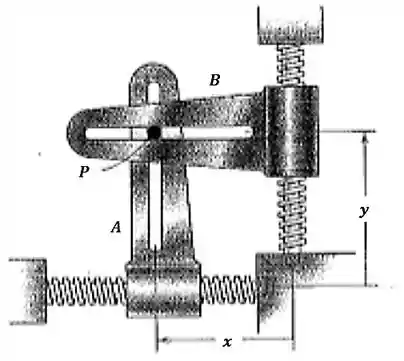
Os movimentos e das guias e com ranhuras em ângulo reto controlam o movimento curvilíneo do pino de conexão, que desliza nas duas ranhuras. Por um curto intervalo de tempo, os movimentos são regidos por , onde e são em milímetros e é em segundos. Calcule o módulo da velocidade e aceleração do pino para . Desenhe a direção da trajetória e indique a sua curvatura para esse instante.

O vetor posição de um ponto que se move no plano é dado por:

Onde é expresso em metros e é expresso em segundos. Determine o ângulo entre a velocidade e a aceleração quando e .

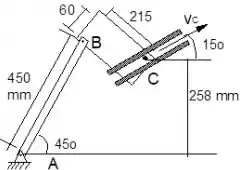
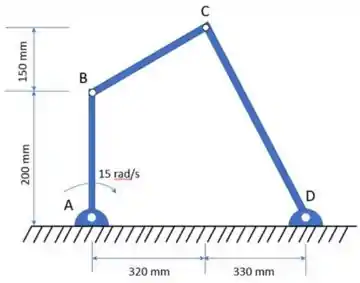
02) Tomando como base a figura a seguir, pede-se:

a) Localize o CIVN da barra BC;

b) Calcule a velocidade angular da barra BC;

c) Calcule a velocidade do ponto C;

d) Calcule a velocidade angular da barra CD;

No mecanismo ilustrado na figura o ponto C se movimenta ao longo de uma guia deslizante. No instante representado a velocidade do ponto C é igual a e está sendo reduzida à taxa de a cada segundo.

Para o instante representado na figura pede-se:

1. Com um desenho do mecanismo, mostrar a localização do centro instantâneo de velocidade nula da caixa conectada nos pontos B e C.
2. A magnitude da velocidade angular da barra é igual a?
3. Em outro desenho, mostrar as componentes dos vetores aceleração dos pontos B e C.
4. A magnitude da aceleração angular da barra AB é igual a?