Coeficiente de Poisson
Produzido por Pablo RicardoTeoria
Seja muito bem vindo ao Responde Aí! Vem entender comigo o que é o Coeficiente de Poisson!
O que é Coeficiente de Poisson?
O Coeficiente de Poisson é uma relação entre as deformações dois eixos.
-Hãm?! 😖
Calma, vamos contextualizar!
Sabe quando você estica um elástico e ele não só aumenta de comprimento como também fica mais fino?
O mesmo fenômeno também acontece com a maioria dos materiais sólidos!
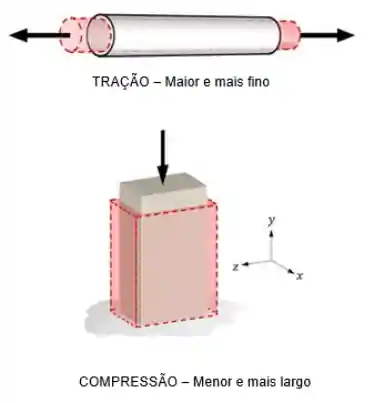
Por exemplo, se você comprime uma coluna de metal, ela não só diminui de tamanho como também fica mais grossa.
É claro que ninguém vai comprimir uma coluna de metal em casa, com as próprias mãos! Mas deu pra pegar o espirito da coisa?! 🤣🤣🤣 Esse conceito vai ser muito importante em vários momentos aqui em Ciências dos Materiais!
Fórmula do Coeficiente de Poisson
A fórmula do Coeficiente de Poisson tem essa carinha aqui:
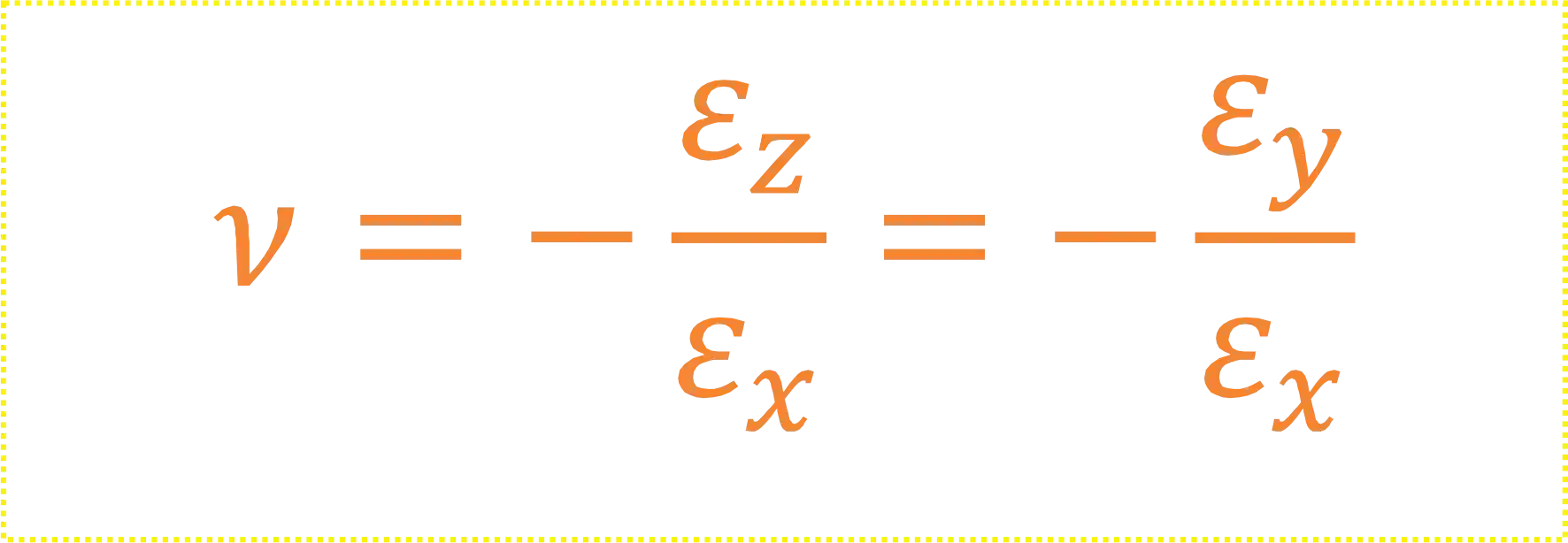
Onde:
é o Coeficiente de Poisson. É um valor adimensional que varia de a dependendo do material; é a deformação ao longo do eixo - eixo ao longo do comprimento da peça; é a deformação ao longo do eixo - eixo lateral do peça; é a deformação ao longo do eixo - eixo lateral da peça.
📢 Clique para ver mais!
Deformação Longitudinal e Lateral
As deformações em cada eixo são dadas por:
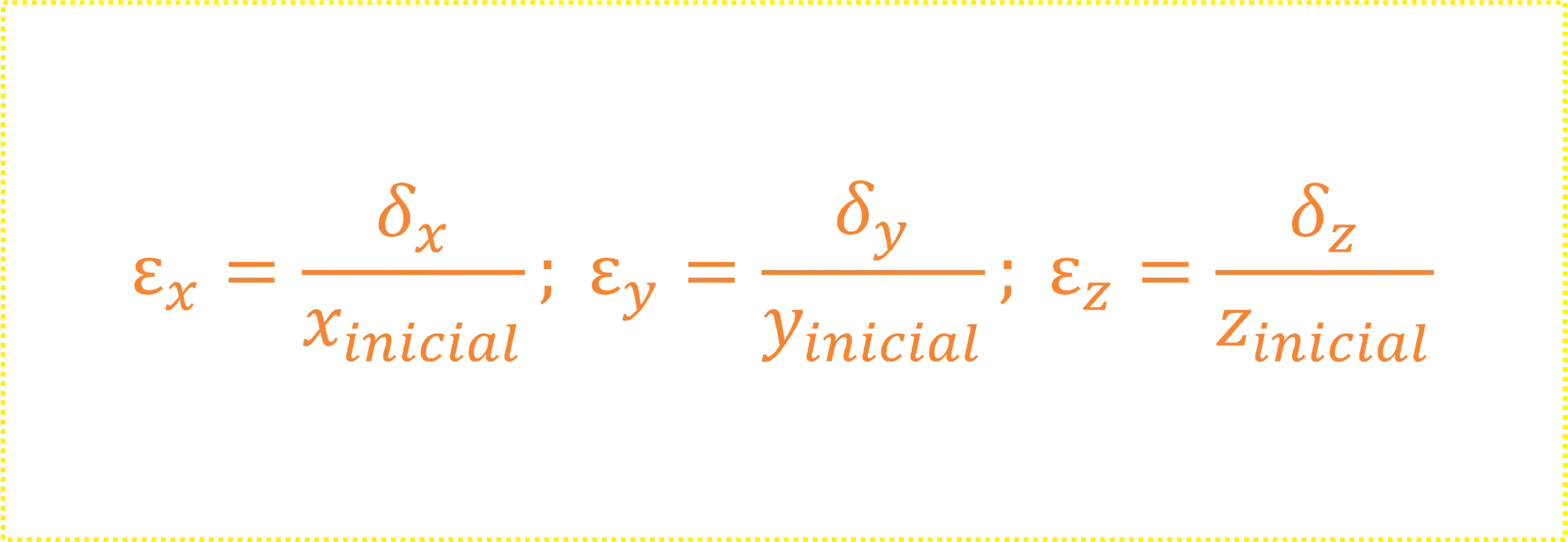
Onde:
, e são as variações que ocorreram nas direções, , e , respectivamente, e; , e são os comprimentos iniciais nas direções , e , respectivamente.
Se está parecendo meio confuso para você, vamos fazer um exemplo para clarear.
Exemplo: Se uma viga com coeficiente de Poisson
Primeiro, vamos ver o que a questão nos fornece:
OBS.: Aqui, a deformação no eixo longitudinal, eixo
E o que a questão pede:
Agora, vamos aplicar a fórmula do Coeficiente de Poisson e achamos o que está sendo pedido:
E prontinho! Viu? Bem de boas!
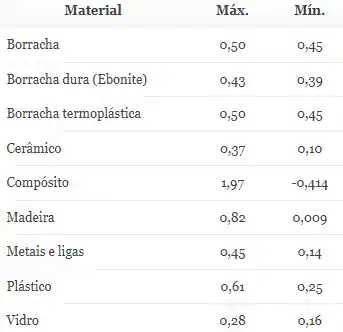
Tabela: Coeficiente de Poisson
O coeficiente de Poisson varia com o material que esta sendo submetido à tensão. Na tabela abaixo podemos conferir alguns valores típicos:
Coeficiente de Poisson: Vídeo Aula
Se você ficou com alguma dúvida, confere esse vídeo sobre Coeficiente de Poisson! 👇
Agora, bora para os exercícios praticar! 😉
Tabela: Coeficiente de Poisson
Coeficiente de Poisson: Vídeo Aula
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Um cabo de aço utilizado em um teleférico possui um diâmetro de . Quando o teleférico está em uso, ele sofre uma deformação ao longo de seu comprimento de .
Sabendo que o aço possui um Coeficiente de Poisson de , estime a variação no diâmetro do cabo de aço quando o teleférico está em uso.
Passo 1
O cabo possui um diâmetro inicial e sofre uma deformação longitudinal, ao longo de seu comprimento, de .
De acordo com o seu coeficiente de Poisson de , essa deformação longitudinal é acompanhada por uma deformação lateral :

Essa deformação lateral é definida como a variação de qualquer medida lateral na peça (como a medida do diâmetro da seção transversal da peça) sobre o valor inicial da medida.
Usando o diâmetro como essa medida, temos:
Juntando essas duas equações, vamos conseguir definir a variação do diâmetro sofrida pelo cabo, que é o que o exercício quer, em função da deformação lateral fornecida de !
Passo 2
Então da definição do coeficiente de Poisson, temos que:
A partir dessa equação a gente pode encontrar a deformação lateral:
Substituindo
Agora podemos encontrar a variação de diâmetro utilizando a equação:
Substituindo:
Perceba que o diâmetro diminuiu
Resposta
Exercício Resolvido #2
Prof. João Chafi Hallack et al., Apostila de Resistência dos Materiais 1, Universidade Federal de Juiz de Fora, Março de 2015, pp. 43-5.
Um cilindro de bronze (), com diâmetro original de e comprimento de , é colocado em uma máquina de compressão e comprimido até que seu comprimento se torne . Determinar o novo diâmetro do bloco.
Passo 1
O cilindro de bronze possui um Coeficiente de Poisson , um diâmetro original e um comprimento original .
Ele é comprimido até um comprimento final , caracterizando nele uma deformação longitudinal (no sentido do comprimento) :
Onde é a variação no comprimento do cilindro, calculada como a diferença entre o comprimento final e o comprimento inicial , tal que:
Agora, de acordo com o Coeficiente de Poisson, essa deformação longitudinal vai ser acompanhada por uma deformação lateral (no sentido do diâmetro do cilindro) :
E assim como é definida como a variação do comprimento dividida pelo comprimento original, pode ser definida como a variação do diâmetro dividida pelo diâmetro original:
Então se calcularmos , vamos poder calcular através da fórmula do Coeficiente de Poisson.
E, conhecendo e o diâmetro original do cilindro, podemos calcular o diâmetro final usando a definição de .
Vamos seguir esses passos para resolver o exercício!
Passo 2
Primeiro, calculamos a deformação longitudinal:
Substituindo e :
O que dá:
Passo 3
Em seguida, calculamos a deformação lateral usando a equação do Coeficiente de Poisson:
Isolando :
Substituindo e :
O que dá:
Passo 4
Por último, usamos a definição da deformação lateral:
Queremos descobrir o diâmetro final , então devemos isolá-lo.
Multiplicando os dois lados por e depois somando aos dois lados, isolamos o diâmetro final :
Para deixar tudo mais bonito, espelhamos a equação e colocamos o diâmetro inicial em evidência:
Substituindo e :
O que dá:
Resposta
Exercício Resolvido #3
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 78-3.26.
A haste plástica de acrílico tem de comprimento e de diâmetro. Se uma carga axial de for aplicada a ela, determine a mudança em seu comprimento e em seu diâmetro.
, 0.
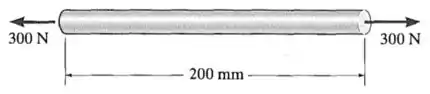
Passo 1
O exercício quer saber a variação do comprimento (tradicionalmente chamada de ) e a variação do diâmetro da haste.
Para encontrar a variação do comprimento, podemos nos lembrar da fórmula que obtemos quando combinamos a Lei de Hooke () com as fórmulas da tensão normal média () e da deformação normal ():
Com essa fórmula, conseguimos calcular a variação do comprimento da haste a partir:
- Da força interna normal , que vai ser igual à carga de tração de ;
- Do comprimento inicial da haste;
- Do módulo de elasticidade do plástico;
- E da área da seção transversal da haste, que pode ser descrita em função de seu diâmetro através da fórmula .
Agora, essa haste não vai sofrer deformação só no sentido longitudinal (sentido do seu comprimento). Ela também vai se deformar no sentido lateral (sentido do seu diâmetro).
O coeficiente de Poisson do plástico vai ditar a razão entre essas deformações e através da fórmula:
A deformação no sentido longitudinal pode ser calculada dividindo a variação do comprimento nesse sentido pelo comprimento original :
Enquanto isso, a deformação no sentido lateral é a divisão da variação de uma medida no sentido lateral pelo valor inicial dessa medida.
Usando o diâmetro como essa medida, temos:
Usando essas três últimas fórmula, vamos poder calcular a variação do diâmetro da haste.
Passo 2
Vamos começar encontrando a variação do comprimento da haste.
Combinando a Lei de Hooke () com as fórmulas da tensão normal média () e da deformação normal (), temos:
Como a área da seção transversal dessa haste é circular, ela pode ser descrita em função de seu diâmetro através da fórmula :
Substituindo os valores , , e :
Reescrevendo como , temos:
Como , as unidades “” e “” nessa equação vão se cortar e o resultado vai sair em milímetros ().
Calculando tudo, encontramos:
Metade do exercício já está resolvido, agora vamos para a próxima metade!
Passo 3
Queremos encontrar a variação do diâmetro da haste.
Da equação do coeficiente de Poisson, temos:
Onde:
Substituindo essas definições na equação do coeficiente de Poisson:
Isolando nessa expressão, encontramos:
Substituindo os valores de , , e :
Calculando tudo, isso dá:
E assim temos as respostas para o exercício:
Resposta
Exercício Resolvido #4
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 119-2.65.
A variação no diâmetro de um grande parafuso de aço é cuidadosamente medida enquanto a porca é apertada. Sabendo que e , determine a força interna no parafuso, quando se observa que o diâmetro diminuiu em .
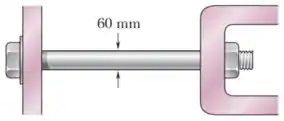
Passo 1
O que está acontecendo?
Ao mesmo tempo que o parafuso faz forças nas peças rosas para manter elas em suas posições, as peças reagem tracionando o parafuso pelas extremidades.
Essa tração significa que existe no parafuso uma força interna normal e uma tensão normal média:
Pela Lei de Hooke, essa tensão corresponde a uma deformação normal/longitudinal no parafuso:
E pela definição do coeficiente de Poisson , essa deformação longitudinal é acompanhada por uma deformação lateral :
Agora, o exercício disse que o parafuso tinha um diâmetro inicial e sofreu uma diminuição de , ou seja, ele sofreu uma variação de diâmetro .
Isso significa que o exercício nos descreveu a variação lateral no parafuso, uma vez que:
E o que é que o exercício quer?
Ele quer saber o valor da força interna normal no parafuso.
Para descobrir esse valor, vamos partir da fórmula da tensão normal média e desenvolver ela usando a Lei de Hooke, a definição do Coeficiente de Poisson e a definição da deformação lateral.
Dessa forma, vamos conseguir descrever a força a partir de valores que conhecemos, como:
- O módulo de elasticidade ;
- O coeficiente de Poisson ;
- O diâmetro inicial ;
- E a variação de diâmetro .
Passo 2
Então primeiro, vamos resolver o exercício literalmente. Em seguida, substituímos os valores e encontramos .
Partindo da fórmula da tensão normal média, temos:
Queremos encontrar , então podemos isolá-lo desde já:
Ok!
Agora, a tensão pode ser descrita pela Lei de Hooke .
E a área da seção transversal do parafuso é circular e pode ser descrita em função de seu diâmetro através da fórmula .
Fazendo essas substituições, temos:
Arrumando a expressão, ela fica assim:
Beleza...
Conhecemos os valores de e , mas não conhecemos o valor da deformação longitudinal .
Mas sabemos descrever a deformação lateral , e sabemos que essas deformações são relacionadas pelo coeficiente de Poisson:
Isolando , temos:
Substituindo isso na última expressão que tínhamos encontrado para :
Arrumando, fica assim:
Agora só falta descrever a deformação lateral .
Ela é a razão entre a variação de uma medida no sentido lateral (como o nosso diâmetro) sobre o valor inicial da medida, ou seja:
Fazendo essa última substituição, a força fica assim:
Simplificando, temos:
Passo 3
Agora, só falta substituir os valores de , , e na expressão que encontramos para :
Fazendo as substituições:
Pausa para olhar para as unidades...
é o mesmo que .
Então se a gente conseguir reescrever a variação de (micrometros) em milímetros (), as unidades de milímetros vão se cortar e o resultado para a força vai sair em .
micrometro é o mesmo que metros ou milímetros, então:
Fazendo essas substituições, a conta fica assim:
Calculando tudo, isso dá:
Resposta
Exercício Resolvido #5
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 119-2.63.
Uma força de tração de é aplicada a um corpo de prova feito de placa de aço plana de (, ). Determine a variação resultante no comprimento de referência de , na largura da parte do corpo de prova, na espessura da parte e na área da seção transversal da parte .

Passo 1
A região do corpo de prova possui, originalmente, um comprimento , uma largura e uma espessura .
O material do corpo de prova possui um módulo de elasticidade e um Coeficiente de Poisson .
Além disso, a força interna normal no corpo de prova é , uma vez que ele está submetido a uma força de tração pura com essa intensidade.
E o que é que o exercício quer?
Por causa da tração, a região é esticada, sofrendo variações no seu comprimento, na sua largura, na sua espessura, e, consequentemente, na sua área de seção transversal.
O exercício quer saber o valor dessas variações.
No item , para encontrar a variação do comprimento, vamos ter que usar a Lei de Hooke e as fórmulas da tensão normal média e da deformação normal.
Nos itens e , para encontrar as variações da largura e da espessura, vamos ter que analisar a deformação lateral na peça.
(Vamos precisar das definições de deformação longitudinal e lateral e das definições do coeficiente de Poisson .)
Finalmente, no item , vamos encontrar a variação da área da seção transversal calculando a diferença entre a área final e a área inicial.
Passo 2
Temos várias informações sobre a peça e sobre o carregamento nela e queremos saber, no item , qual é o valor da variação de comprimento sofrida pela região do corpo de prova.
Normalmente, chamamos essa variação de comprimento principal de .
Agora, lembra aí...
Existe uma fórmula que descreve a variação de comprimento numa peça em função do carregamento nela:
E a fórmula que obtemos quando combinamos a Lei de Hooke com as fórmulas da tensão normal média e da deformação normal.
Nessa fórmula, sabemos o valor de , e , mas não sabemos o valor da área da seção transversal da região .
Mas sabemos que essa região tem uma seção transversal retangular, de espessura e largura . Logo:
Sendo assim, a variação de comprimento fica assim:
Pronto, agora podemos calcular o valor da variação de comprimento !
Substituindo os valores de , , , e , temos:
Reescrevendo como e reescrevendo a força de como :
Agora, as unidades e vão se cortar, e o resultado final vai sair em .
Calculando tudo, temos que:
Passo 3
Agora, seguimos para os itens e .
Nesses itens queremos encontrar a variação de largura e a variação de espessura na parte do corpo de prova.
Essas duas variações ocorrem por causa da deformação lateral que acompanha toda deformação longitudinal num corpo.
A deformação longitudinal é aquela que ocorre no sentido do comprimento do corpo. É a variação de comprimento sobre o comprimento inicial:
E a deformação lateral é a que ocorre no sentido lateral. É a variação de uma medida da seção transversal da peça (como a largura ou a espessura) sobre a medida inicial:
E essas duas deformações são relacionadas pelo coeficiente de Poisson:
O que significa que:
E, como :
Substituindo e isolando , encontramos:
E, alternativamente, substituindo e isolando , temos:
Pronto, encontramos as expressões que vão nos dar os valores de e !
Substituindo os valores de , , , e nessas duas expressões, temos:
Calculando tudo, encontramos:
Passo 4
Por último, resolvemos o item , onde queremos encontrar a variação de área de seção transversal na parte do corpo de prova.
A variação de qualquer medida é igual ao seu valor final menos o seu valor inicial.
Então sendo o valor final da área da seção transversal, temos que:
A seção transversal é retangular, de espessura e largura , de tal forma que .
A seção transversal final também vai ser retangular, de espessura final e largura final , de tal forma que .
Ou seja:
Agora, a espessura e a largura final vão ser iguais aos seus valores iniciais mais as suas variações:
Substituindo isso na expressão anterior, temos:
Substituindo os valores de , , e , todos em milímetros:
Calculando tudo:
E assim finalizamos o exercício:
Resposta
Exercício Resolvido #6
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 79-3.33.
O tampão tem diâmetro de e ajusta-se ao interior de uma luva rígida com diâmetro interno de . Ambos, tampão e luva, têm de comprimento.
Determine a pressão axial que deve ser aplicada à parte superior do tampão para que ele entre em contato com as laterais da luva. Determine também a que distância o tampão deve ser comprimido para baixo para que isso aconteça.
O material do tampão tem e .
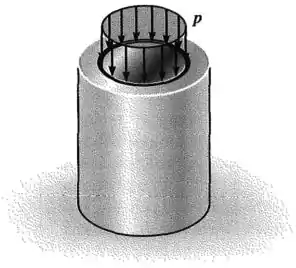
Passo 1
O que está acontecendo?
O tampão tem um diâmetro inicial e um comprimento inicial .
O seu material tem um módulo de elasticidade e um Coeficiente de Poisson .
E ele está submetido a uma pressão axial de compressão.
Agora vamos pensar...
Pressão é força sobre área, então essa pressão pode ser trocada por uma força equivalente , onde é a área da seção transversal do tampão.
Essa força de compressão vai gerar no tampão uma força interna normal e uma tensão normal média:
Substituindo , temos:
Ou seja, para o equilíbrio interno do tampão, a tensão tem que ser o oposto da pressão .
E o que é que o exercício quer?
Ele quer saber qual é a pressão que faz com que o tampão encoste nas laterais da luva.
Ou seja, ele quer saber qual é a pressão que faz com que o diâmetro final do tampão seja igual ao diâmetro interno de na luva.
Agora, Para que o tampão tenha esse diâmetro final , ele tem que ter sofrido:
- Uma certa deformação lateral ;
- Uma certa deformação longitudinal , de acordo com seu coeficiente de Poisson ;
- E uma certa tensão normal média , de acordo com a Lei de Hooke .
Então combinando a Lei de Hooke, as definições do coeficiente de Poisson e da deformação lateral e a relação , vamos poder relacionar a pressão com o diâmetro final e encontrar o valor de que garante que .
Depois, o exercício ainda quer que a gente encontre a variação de comprimento que o tampão sofreu.
Para tanto, vamos ter que usar a definição , a Lei de Hooke (para encontrar a deformação correspondente a uma certa tensão normal ) e a relação .
Passo 2
Queremos relacionar então a pressão axial no tampão com o seu diâmetro final .
Para tanto, vamos começar usando a Lei de Hooke:
Aplicando a relação , temos:
Agora, vamos pensar...
Precisamos relacionar não com a deformação longitudinal , mas sim com a deformação lateral no tampão, já que é a deformação lateral que causa a variação no diâmetro do tampão.
Para encontrar em função de , usamos a definição do Coeficiente de Poisson :
Isolando , temos:
Substituindo essa expressão na equação que tínhamos encontrado anteriormente, temos:
Agora, só falta descrever essa deformação lateral em função do diâmetro final que vamos obter uma expressão para a pressão em função de .
A deformação lateral é definida como a variação de uma medida no sentido lateral (como o diâmetro, por exemplo) sobre o valor original da medida, ou seja:
Substituindo isso na última expressão que tínhamos encontrado para , temos que:
Passo 3
Agora que já encontramos uma expressão que relaciona a pressão axial no tampão com o seu diâmetro final :
podemos substituir os valores , , e nessa expressão para descobrir qual é a pressão axial que faz com que o tampão encoste nas laterais da luva:
Calculando tudo, isso dá:
Esse é um número pequeno, então fica melhor reescrevê-lo em :
Passo 4
Já resolvemos a primeira parte do exercício, que foi encontrar a pressão que faz com que o tampão tenha um diâmetro final .
Agora, queremos resolver a segunda parte: descobrir a distância que o tampão teve que ser comprimido para baixo para que isso aconteça.
Essa distância é a variação de comprimento do tampão, que é descrita pela sua deformação longitudinal :
Onde e é o seu comprimento original de do tampão.
Isolando nessa definição de , temos:
A gente não conhece o valor de , mas a gente sabe que essa deformação é proporcional à tensão normal média no tampão de acordo com a Lei de Hooke:
Mas como vimos no primeiro passo, , então:
Substituindo isso na expressão que tínhamos encontrado para a variação de comprimento , ela fica assim:
Então substituindo nessa equação , vamos descobrir qual é a variação de comprimento que corresponde a essa situação.
Fazendo essa substituição e ainda substituindo os valores de e , temos:
Para que o resultado saia em milímetros (), reescrevemos o módulo de elasticidade de como :
Calculando, encontramos:
Ou seja, o tampão teve que ser comprimido para baixo para que ele encostasse nas laterais da luva.
Resposta
Exercício Resolvido #7
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 119-2.64.
Um tubo de aço de comprimento igual a , diâmetro externo de e espessura de parede de é usado como uma coluna curta e suporta uma força axial centrada de .
Sabendo que e , determine a variação no comprimento do tubo, a variação em seu diâmetro externo e a variação na espessura da parede.
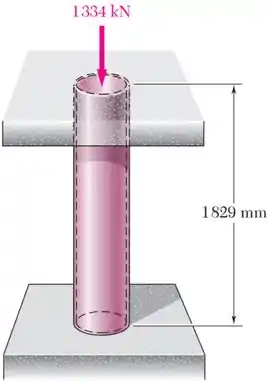
Passo 1
O tubo tem, inicialmente, um comprimento , um diâmetro externo e uma parede de espessura .
Além disso, o tubo é feito de um aço de módulo de elasticidade e Coeficiente de Poisson .
Quando o tubo for carregado com a força de compressão de , vai surgir nele uma força interna normal , que vai gerar nele uma tensão normal média .
De acordo com a Lei de Hooke e o Coeficiente de Poisson, essa tensão normal no tubo vai ser acompanhada por deformações longitudinal e lateral .
E o que é que o exercício quer?
Ele quer que a gente determine as variações de comprimento , de diâmetro externo e de espessura da parede no tubo quando ele é carregado com a força de .
Para encontrar a variação de comprimento do tubo no item , podemos usar a fórmula que vem da combinação da Lei de Hooke com as fórmulas da tensão normal média e da deformação normal:
Já para encontrar as variações do diâmetro externo e da espessura da parede nos itens e , vamos precisar nos lembrar da definição de deformação lateral:
A deformação lateral é definida como a variação de uma medida no sentido lateral (como o diâmetro ou a espessura do tubo) sobre o valor inicial dessa medida.
Ou seja:
Então se conseguimos usar o Coeficiente de Poisson para encontrar , vamos conseguir encontrar em seguida e .
Passo 2
Vamos começar resolvendo o item .
Aplicando a fórmula que descreve a variação de comprimento de uma peça a partir do carregamento axial na peça, temos:
Sabemos que , e , mas não sabemos o valor da área da seção transversal do tubo.
Então vamos olhar para a seção transversal do tubo para encontrar sua área :
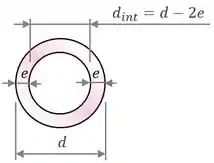
Vemos que dá pra definir a área como a diferença entre a área do círculo de diâmetro externo e a área do círculo de diâmetro interno .
A área de cada um desses círculos vai ser dada pela fórmula , então:
Colocando em evidência, encontramos que:
Podemos deixar essa área em função do diâmetro interno uma vez que pode ser calculado facilmente:
Passo 3
Encontrada uma expressão para a área , podemos substituir ela na fórmula :
Arrumando tudo, isso fica assim:
Agora, só falta substituir os valores de , , , e para encontra o valor da variação de comprimento sofrida pelo tubo.
Fazendo todas essas substituições, temos:
Como , as unidades e nessa equação vão se cortar, e o resultado final vai sair em milímetros ().
Calculando tudo, encontramos:
Que é a resposta do item !
Passo 4
Agora, antes de resolver os itens e , vamos encontrar a deformação lateral no tubo, já que é ela que descreve as variações do diâmetro externo e da espessura da parede .
A deformação lateral aparece na fórmula do Coeficiente de Poisson, então vamos começar usando essa fórmula:
Isolando a deformação lateral , temos:
Como a deformação longitudinal é definida como a variação de comprimento sobre o comprimento original , temos que:
Conhecemos , e , então encontramos a deformação lateral no tubo!
Passo 5
No passo anterior, encontramos que:
Agora, podemos usar isso para resolver os itens e .
Começando pelo item ...
Queremos encontrar a variação do diâmetro externo , então definimos a deformação lateral como:
Substituindo isso na expressão que encontramos no passo anterior, temos que:
Isolando :
Inserindo os valores de , , e :
O que dá:
Ou se preferirmos:
Passo 6
Finalmente, para o item , repetimos o que fizemos para o item :
Queremos encontrar a variação da espessura da parede , então definimos como:
Substituindo isso na expressão do passo anterior, temos que:
Inserindo os valores de , , e , encontramos a variação da espessura da parede :
Ou em notação científica:
Resposta
Exercício Resolvido #8
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 120-2.69.
Um tecido utilizado em estruturas infláveis está submetido a um carregamento biaxial que resulta em tensões normais e . Sabendo que as propriedades do tecido podem ser de aproximadamente e , determine a variação no comprimento do lado , do lado e da diagonal .
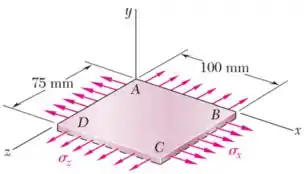
Passo 1
Nos exercícios anteriores, a gente sempre trabalhou com só uma tensão normal e com as deformações longitudinal e lateral .
Agora, nesse exercício, nós temos tensões multiaxiais:
- No eixo , temos uma tensão normal ;
- No eixo , não temos tensão normal, então ;
- E no eixo , temos uma tensão normal .
Por esse motivo, ao invés de usarmos as deformações longitudinal e lateral em exercícios como esse, usamos as deformações em cada eixo: , e .
E como a gente encontra essas deformações em cada eixo?
Lembra aí!
Existem fórmulas para as deformações em cada eixo como consequência das tensões multiaxiais:
Cada uma dessas fórmulas é o resultado da soma dos efeitos que as tensões em cada eixo têm na deformação em uma certa direção.
Beleza, e o que é que o exercício quer?
Ele quer saber:
A variação no comprimento do lado , .
Como o lado está ao longo do eixo , essa variação vai ser definida pela deformação em :
onde é o comprimento inicial de do lado .
A variação no comprimento do lado , .
está ao longo do eixo , então:
Onde é o comprimento inicial de do lado .
A variação no comprimento da diagonal , .
Não existe uma “deformação diagonal” que define a variação de , mas podemos pensar nessa variação assim:
Inicialmente, a diagonal tem um comprimento que pode ser encontrado a partir do Teorema de Pitágoras:
Enquanto que, ao final, o lado vai ter um comprimento e o lado um comprimento , de tal forma que a diagonal vai ter um comprimento final :
E assim a variação vai ser dada por:
Então, resumindo...
Se encontramos as deformações em e em ( e ), vamos poder calcular as variações e , resolvendo os itens e .
E, conhecendo as variações e , conseguimos calcular a variação da diagonal, , resolvendo assim o item .
O material tem um módulo de elasticidade e um coeficiente de Poisson .
Passo 2
Então vamos começar o exercício encontrando as deformações em e em ( e ).
Usando as fórmulas para a deformação em e em em situações de tensões multiaxiais, temos:
Como, no nosso caso, a tensão normal em é igual a zero, temos que:
O exercício nos forneceu o valor do módulo de elasticidade em , sendo que as tensões e foram fornecidas em .
Para que os nossos resultados de deformação sejam adimensionais, vamos reescrever o módulo de elasticidade em na hora de substituir o seu valor.
Substituindo os valores de , , e , temos:
Calculando tudo, encontramos:
Passo 3
Agora que sabemos as deformações em e em , podemos resolver os itens e .
Começando pelo item :
Podemos definir a deformação em como:
Como queremos encontrar no item a variação do comprimento do lado , devemos isolar :
Substituindo os valores de e , temos:
O que dá:
Passo 4
E agora para o item :
Queremos encontrar a variação do comprimento do lado , que é descrita pela deformação em :
Isolando , temos:
Substituindo os valores de e :
O que dá:
Passo 5
Por último, resolvemos o item :
Queremos encontrar a variação de comprimento da diagonal .
Toda variação de comprimento é igual ao comprimento final menos o comprimento inicial, logo:
O comprimento inicial pode ser encontrado através do Teorema de Pitágoras, usando os lados e como os catetos e o lado como a hipotenusa:
Da mesma forma, o comprimento final também pode ser calculado através do Teorema de Pitágoras.
Mas, dessa vez, os lados e vão ter seus comprimentos finais, que vão ser iguais aos seus comprimentos iniciais mais as variações de comprimento sofridas:
Dessa forma, temos que:
Substituindo todos os valores, temos:
O que dá:
Resposta
Exercício Resolvido #9
Elaboração Própria
Uma pequena esfera de acrílico de diâmetro afundou no oceano até um ponto com uma pressão de . Sabendo que o acrílico tem um módulo de elasticidade e um Coeficiente de Poisson , determine a variação no diâmetro dessa esfera.
Passo 1
A esfera tem um diâmetro inicial , um módulo de elasticidade e um Coeficiente de Poisson .
O exercício quer saber a variação no diâmetro que a esfera sofre ao estar submetida a uma pressão .
Então vamos pensar...
Quando alguma peça está submergida na água (ou qualquer outro fluído), a água faz pressão na peça por todos os lados.
Isso quer dizer que se a peça está em um ponto em que a pressão é , a peça está submetida a uma pressão de no seu eixo , no seu eixo e no seu eixo .
(O nome disso é pressão hidrostática.)
Agora pensa só...
Pressão é força sobre área que nem tensão é força interna sobre área.
Então se uma força de compressão gera numa peça uma força interna normal , uma pressão de compressão gera uma tensão normal .
Então como reação interna à pressão de nas dimensões, vão surgir na peça tensões normais nos eixos , e , todas iguais ao oposto da pressão de compressão:
Isso quer dizer que a esfera está em uma situação de carregamento multiaxial em que todas as três tensões são igual a .
Como consequência de um carregamento multiaxial, uma peça sofre deformações em , e , de acordo com as fórmulas:
Mas no nosso caso, se substituirmos nessas deformações, vamos encontrar que todas elas são iguais:
Normalmente, o é tirado em evidência...
...e essa equação é arrumada para ficar assim:
Então podemos descobrir a deformação sofrida pela esfera usando a fórmula acima...
E como o diâmetro é uma medida que existe nos três eixos em uma esfera, podemos definir todas as deformações assim:
E, em seguida, podemos usar essa definição para encontrar a variação do diâmetro da esfera, resolvendo assim o exercício!
Passo 2
Então primeiro, vamos encontrar a deformação na esfera.
Usando a fórmula que encontramos para descrever a deformação numa peça em função da pressão a qual ela está submetida em todas as direções, temos:
Subsituindo , e , temos:
Para que o resultado da deformação saia adimensional, reescrevemos o módulo de elasticidade de como :
Calculando tudo, encontramos:
Passo 3
Agora que encontramos a deformação na esfera, podemos defini-la em função da variação do diâmetro e do diâmetro inicial da esfera para encontrarmos :
Substituíndo , temos:
Isolando :
E, finalmente, substituindo :
O que dá:
Resposta
Exercício Resolvido #10
Elaboração própria
Abaixo é dado um paralelepípedo de concreto submetido aos carregamentos mostrados na figura. Sabendo que , de termine a deformação em mm de cada lado do paralelepípedo.
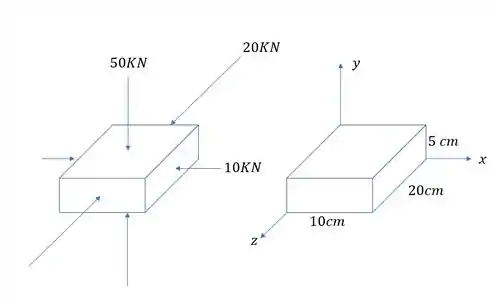
Passo 1
Esse problema se trata de um problema em que temos que usar a fórmula de deformação nos eixos. A fórmula que temos que usar é a fórmula da lei generalizada de Hooke que é dada por
Outro cuidado que temos que tomar é que essas fórmulas dão a deformação especifica em cada eixo, e o enunciado pede a de formação total, ou seja, precisaremos saber que a relação entre deformação especifica e total é dada por
Como o objetivo é determinar a deformação total podemos escrever essa fórmula como
Agora que já definimos quais fórmulas usar, devemos determinar cada parte da fórmula.
Passo 2
Vamos primeiro determinar as tensões em cada um dos eixos. Sabemos que a fórmula que nos dá as tensões em cada eixo é
Vale prestar atenção que todas as cargas aplicadas na nossa peça são cargas de compressão, logo todos os normais devem possuir sinal de menos. Com isso teremos que
Também precisamos determinar as áreas relativas a cada um dos normais.
Agora é fácil determinar o valor das tensões em cada face do nosso paralelepípedo
Passo 3
Já com as tensões em mãos basta determinar as deformações especificas, tomando, é claro, cuidado com os sinais que determinamos, logo teremos que
Em que
Substituindo teremos que
Passo 4
Como eu disse é pedido a deformação total e não especifica, ou seja, temos que usa a seguinte fórmula.
Nos foi pedido também a deformação em mm, logo temos que garantir que esses comprimentos estarão corretor também, logo teremos que.
Substituindo teremos que
Com isso podemos deduzir que os eixos y e z sofreram compressão enquanto que o eixo x sofrerá uma expansão, mesmo atuando no eixo x uma carga de compressão.
Isso ocorre pois as deformações nos eixos y e z são maiores que as deformações de compressão em x, obrigando, nesse caso, o eixo x expandir.