Tensões Principais
Teoria
Introdução
Nos dois últimos tópicos, nós vimos:
- Como definir um estado plano de tensões, como o da imagem abaixo:
- E como utilizar a transformação de tensões para descobrir as tensões , e nesse elemento caso ele fosse rotacionado por um ângulo :
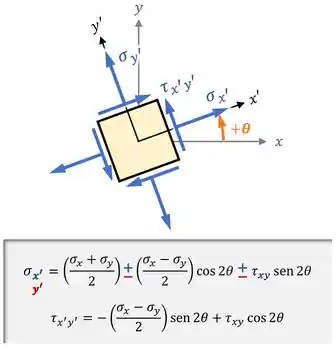
E beleza...
Pode ser muito legal ficar desenhando esses quadradinhos com essas setinhas...
Mas na real que a gente ainda não viu a aplicação prática de tudo isso!
Felizmente, isso vai mudar hoje.
A partir de agora, vamos deixar de sermos aprendizes e vamos nos tornar mestres:
Então vamos lá!
Problema de Exemplo
Vamos dizer que você é um(a) engenheiro(a) aeronáutico(a) e descobriu que, no ponto mais crítico do seu avião, ele está submetido a um estado de tensões:
Como na imagem abaixo:
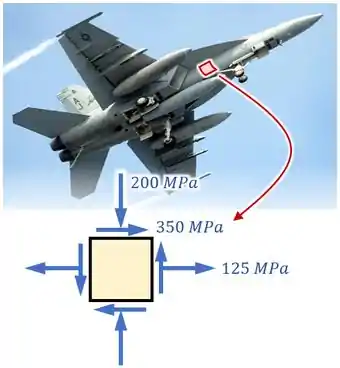
Além disso, você sabe também que o material dessa parte do avião é um material que falha sempre por causa da tensão normal .
Então, para saber se esse ponto vai falhar, você quer descobrir qual é a tensão normal de maior intensidade nesse ponto.
De início, você acha que a tensão normal de maior intensidade nesse ponto é a de .
Mas aí, você recebe uma mensagem do além.
E aí você percebe:
Pera aí.
não é necessariamente a tensão normal de maior intensidade.
Se eu rotacionar meu elemento, eu posso encontrar pelas equações da transformação de tensões outras tensões normais ou que podem ter uma intensidade ainda maior.
Então...
Qual é realmente a tensão normal de maior intensidade nesse ponto?
Como podemos encontrar ela?
Tensões Principais
Justamente para responder essas perguntas, um pessoal decidiu estudar as equações da transformação de tensões.
Eles pensaram:
- Girando o elemento, nós conseguimos converter tensão cisalhante em tensões normais e vice-versa.
- Então se a gente conseguir zerar a tensão cisalhante, vamos ter uma situação com o máximo de tensões normais.
E foi isso que eles fizeram.
Primeiro, chamaram essas tensões normais “máximas” de tensões principais.
Depois, igualaram a fórmula de a zero:
...dividiram tudo por e isolaram a que apareceu.
Assim, descobriram que os ângulos “” que zeram a tensão cisalhante e fazem aparecer as tensões principais são dados pela fórmula:
Fórmula das Tensões Principais
Aí, colocando esses ângulos na fórmula de e manipulando ela bem muito, encontraram uma fórmula para as tensões principais:
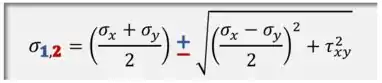
Sendo que:
- é chamada de “tensão principal máxima” e é chamada de “tensão principal mínima”;
- E a diferença entre as fórmulas de e está em ter, respectivamente, o sinal de positivo () ou negativo () entre o termo fora da raíz e a raíz.
Além disso...
Para ficar mais fácil de decorar essa fórmula, algumas pessoas chamam o primeiro termo dela de “”:
E o segundo termo de “”:
Encontrando assim que:
Exemplo de Aplicação
Para o estado de tensões do nosso avião, por exemplo, podemos calcular os valores de , , e :
E assim, vemos como a tensão normal de maior intensidade naquele ponto do avião é uma tensão de compressão de .
Beleza!
Mas e se eu quiser saber qual é a orientação que causa essas tensões principais?
Aí eu posso recorrer à fórmula que vimos anteriormente dos ângulos que fazem essas tensões aparecer:
Mas e esse ângulo , será que ele é o que causa a tensão principal ou a tensão principal ?
Só há um jeito de descobrir: testando!
Pegamos a fórmula de e substituímos esse ângulo:
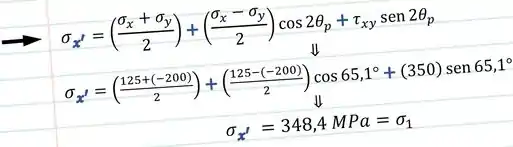
Fazendo isso, vamos como esse ângulo é responsável pela tensão principal , então chamamos ele de “”:
E o ângulo que causa a outra tensão principal ?
Aí é só adicionar ou retirar do primeiro, como foi feito a seguir:
E pronto!
Esses ângulos e são as orientações que causam as tensões principais e e zeram a tensão de cisalhamento:
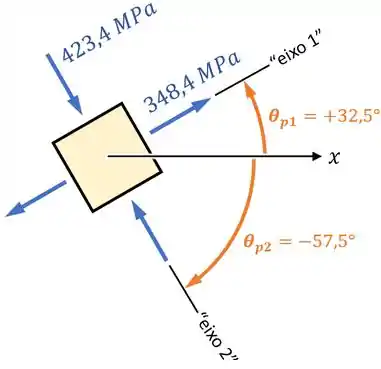
Tensão de Cisalhamento Máxima
E se o material do nosso avião não fosse um material que falhasse sempre por tensão normal , mas sim um material que falha sempre por tensão de cisalhamento ?
Nesse caso...
Lembrando que girando o elemento, nós conseguimos converter tensão cisalhante em tensões normais e vice-versa...
Percebemos que deve existir uma orientação do elemento em que a tensão de cisalhamento tem o seu valor máximo.
E essa orientação existe mesmo!
Ela pode ser obtida somando OU subtraindo de qualquer um dos ângulos .
Por exemplo:
Subtraindo de , encontramos que um ângulo “” que faz com que tenha seu valor máximo é:
E como ficam as tensões nessa orientação?
Então...
Nessa orientação, a tensão de cisalhamento vai ser máxima e pode ser calculada de uma das duas formas abaixo:
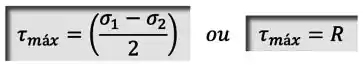
Sendo que se você substituir e na primeira fórmula, você vai acabar encontrando a segunda.
Ou seja, as duas fórmulas dizem a mesma coisa.
Já as duas tensões normais e nessa orientação vão assumir o valor , que pode ser calculado a partir das tensões e OU a partir das tensões principais.
Ou seja:
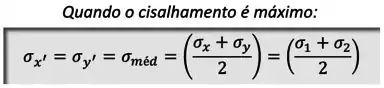
Para o ponto do nosso avião, por exemplo:
Como já calculamos e , podemos usar e para encontrarmos que:
Dessa forma, o desenho do nosso ponto nessa orientação fica assim:
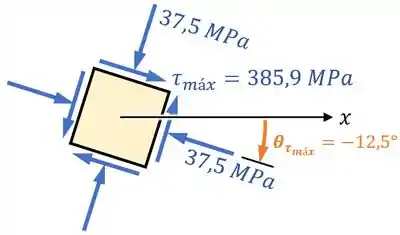
Finalização
Agora é com você!
Você pode treinar seus conhecimentos fazendo alguns exercícios resolvidos a seguir.
Como você pode também aproveitar que você está manjando essa matéria para passar os seus conhecimentos adiante para um(a) outro(a) jovem aprendiz:
Tensões Principais
Fórmula das Tensões Principais
Exemplo de Aplicação
Tensão de Cisalhamento Máxima
Finalização
Exercícios Resolvidos
Exercício Resolvido #1
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 333-9.13.
O estado de tensão em um ponto é mostrado no elemento. Determine as tensões principais e a tensão de cisalhamento máxima no plano e a tensão normal média no ponto. Especifique a orientação do elemento em cada caso.
Passo 1
O que está acontecendo?
O exercício nos fornece um estado plano de tensões em que:
Lembrando que tem um valor negativo nesse caso pois a sua direção no desenho está no sentido oposto ao da convenção, a convenção de sinais é a seguinte:
Observe que as tensões normais são trativas e a tensão cisalhante tem aquela direção apontada no desenho. Isso significa que a tensão fornecida é compressiva!
E o que é que o exercício quer?
No item , ele quer saber as tensões principais e e as orientações e correspondentes.
E no item b?
Já no item , o exercício quer saber a tensão de cisalhamento máxima nesse elemento, além da tensão normal média e da orientação correspondente.
Para tanto, podemos aproveitar que já calculamos e durante a resolução do item anterior.
Enquanto que uma ou mais orientações podem ser obtidas somando OU subtraindo de ou .
Passo 2
Depois de já termos definido o estado plano de tensões no passo anterior:
Já estamos prontos para iniciar a determinação das tensões principais para o item !
Começamos calculando :
E :
Em seguida, já calculamos e :
Passo 3
Agora, para complementar a resposta do item , precisamos determinar as orientações e .
Começamos aplicando:
Aí, utilizando a função da calculadora, encontramos:
O que significa que:
Pessoal, a gente pode visualizar as tensões e juntamente com o ângulo no nosso estado plano de tensões:
Passo 4
Agora, precisamos testar esse valor de para descobrirmos qual é a tensão principal que ele causa.
Para tanto, empregamos a fórmula da transformação de tensões para :
Substituindo todos os valores, temos:
O que dá:
O que é igual à .
Dessa forma, concluímos que é na realidade o ângulo :
E o ângulo ?
Podemos encontrar ele somando ou subtraindo de .
Normalmente, evitamos encontrar ângulos fora do intervalo , então vamos subtrair de para encontrarmos que:
E pronto!
Resolvemos o item por completo.
Passo 5
Em seguida, para o item , podemos aproveitar os valores “” e “” que já calculamos para o item , conforme vimos lá no passo 1.
Para saber a tensão de cisalhamento máxima , podemos aproveitar que para encontrarmos que:
Enquanto que para , podemos aproveitar diretamente o valor que já calculamos lá no passo 2 :
Por fim, para encontramos orientações em que essa tensões e ocorrem, podemos somar OU subtrair de OU .
Evitando encontrar ângulos fora do intervalo , encontramos dessa forma que:
E assim completamos nossa resposta para o item !
Resposta
Exercício Resolvido #2
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 511-7.161.
O tubo de aço tem de diâmetro externo e uma espessura de parede de . Sabendo que o braço está rigidamente fixado ao tubo, determine as tensões principais e a tensão de cisalhamento máxima no ponto .
Passo 1
O que está acontecendo?
O tubo tem:
- Um diâmetro externo e consequentemente um raio externo ;
- E uma parede de espessura , e consequentemente um raio interno .
A força de é aplicada no braço , resultando no aparecimento de vários esforços internos ao longo do tubo .
E o que é que o exercício quer?
Ele quer saber as tensões principais e e a tensão máxima de cisalhamento no ponto .
Daí que, para encontramos isso, vamos ter que:
1. Realizar uma análise dos esforços internos na seção em que se encontram os pontos e , com o objetivo de descrever os esforços internos nessa seção.
2. Para cada um dos esforços internos encontrados no passo anterior, calcular e verificar o sentido da tensão causada por esses esforços interno.
3. Juntar os resultados dos passos anteriores para desenhar o estado plano de tensões para o ponto , definindo assim as tensões , e nele.
E finalmente, 4. Calcular e utilizando as fórmulas:
Para depois determinarmos as tensões principais , e a tensão de cisalhamento máxima nesse ponto!
Passo 2
Então vamos começar pela análise dos esforços internos.
Precisamos secionar o tubo na seção em que se encontram os pontos e .
Fazendo o uso de um desenho simplificado do conjunto e fazendo essa seção, vamos ter:
Aí, agora, temos que nos lembrar dos possíveis esforços internos que podem existir nessa seção:
- Força Normal ;
- Força Cortante , que para essa seção em um conjunto em como esse, pode existir tanto ao longo do eixo quanto ao longo do eixo ;
- Torque Interno , que também pode ser chamado de momento torsor ou de momento em volta do eixo , ;
- E momentos fletores ou , que para essa seção em um conjunto em como esse, pode existir tanto em volta do eixo quando em volta do eixo .
Mas aí...
Percebendo que a única força externa na nossa peça é a força de , percebemos que ela não vai gerar:
- Nenhuma força normal ;
- Nenhuma força cortante ao longo do eixo ;
- & nenhum momento fletor em volta do eixo .
Então os nossos esforços internos na nossa seção vão ficar assim:
Passo 3
Agora, podemos aplicar o equilíbrio no desenho que fizemos no passo anterior para encontrarmos o valor de cada esforços interno.
Começando pelo equilíbrio de forças no eixo , temos:
O que significa que:
Seguindo com o equilíbrio de torques para o nosso tubo , temos:
Aí aqui, vamos ter dois torques no nosso tubo:
- o torque interno , que desenhamos de forma a estar no sentido oposto do eixo (sentido negativo);
- e o torque gerado pela força de com um braço de , que pela regra da mão direita vai estar no sentido do eixo (sentido positivo).
Dessa forma, o nosso somatório de torques fica assim:
O que significa que:
Ou, em :
Para finalizar, utilizamos o equilíbrio de momentos em relação ao ponto da seção:
Aqui, vamos ter o momento fletor no sentido anti-horário () e um momento gerado pela força de com um braço de no sentido horário ().
Então, nosso somatório fica assim:
Isolando , encontramos:
Ou, em :
Passo 4
Chegou a hora de calcular e avaliar o sentido de cada tensão causada por cada um desses esforços internos.
Começando pela força de cisalhamento :
Sabemos que a tensão de cisalhamento causada por uma força de cisalhamento é nula no topo e na base de uma seção.
E, nesse nosso caso, nós temos uma força de cisalhamento ao longo do eixo .
E, ao longo do eixo , o nosso ponto está efetivamente no topo da seção:
Então...
A tensão de cisalhamento devido a força de cisalhamento é nula no ponto .
Passo 5
Seguindo com o torque interno .
Pelo que estudamos lá em torção, sabemos que ele vai causar uma tensão de cisalhamento nos pontos da nossa seção de acordo com a fórmula:
Onde:
- é a distância entre o centro da seção e o ponto em que queremos avaliar a tensão (no nosso caso, o ponto , que está na superfície externa do tubo de tal forma que );
- & é o momento polar de inércia, que podemos calcular para um tubo vazado como:
Sendo que, substituindo e , isso dá:
Aí, aplicando a fórmula da torção para o nosso ponto , temos:
E substituindo , e , encontramos que:
Finalmente, calculando tudo e sabendo que é o mesmo que , encontramos que:
Passo 6
Agora, antes de seguir para a tensão causada pelo momento fletor , temos que entender o sentido dessa tensão causada pelo torque interno .
Para tanto, podemos olhar para a forma como desenhamos nosso torque interno lá no passo 2, mas dessa vez também olhando para o posicionamento de em relação à esse torque:
Aí, usando a regra da mão direita:
...conseguimos visualizar como é o sentido desse torque e da tensão causada por ele:
Assim, percebemos que o cisalhamento causado pelo torque no ponto aponta para a esquerda na aresta inferior do elemento :
Mas aí, nós já estudamos também como um cisalhamento em uma aresta tem que ser equilibrado por cisalhamentos em outras arestas, de forma a não provocar um movimento do ponto .
Dessa forma, o cisalhamento no ponto fica assim:
Passo 7
Por fim, chegamos a tensão causada pelo momento fletor .
Sabemos que um momento fletor causa em uma seção tensões normais de acordo com a fórmula da flexão:
Onde:
- é a posição do ponto em que se quer medir a tensão (nesse caso, o nosso ponto ) em relação à linha neutra/centróide da seção;
- & é o momento de inércia da área da seção, que para uma seção circular vazada é dado pela fórmula:
Dessa forma, substituindo e , vamos encontrar que:
Aí, na hora de aplicarmos a fórmula da flexão para o nosso ponto , podemos aplicá-la em módulo:
Isso porque, como estamos lidando com um problema 3D, a fórmula da flexão não é confiável para fornecer o sinal da tensão .
É mais seguro calcular a intensidade de e depois olhar com calma para a forma que desenhamos o momento para descobrirmos se ele causa tração ou compressão no ponto .
Então vamos lá!
Aplicando a fórmula da flexão para , temos:
Aí, substituindo:
- ;
- , uma vez que a linha neutra/centroide da nossa seção circular vazada está bem no meio da seção enquanto que o nosso ponto está na superfície externa da seção;
- & ,
Vamos ter que:
Finalmente, calculando tudo isso e sabendo que é o mesmo que , encontramos que:
Passo 8
Falta entendermos o sentido dessa tensão , então vamos olhar para a forma como desenhamos nosso momento fletor :
Olhando para essa figura, percebemos que o momento comprime o ponto ao longo da vertical (eixo ).
Dessa forma, temos que:
Sendo que o sinal de negativo indica que essa tensão é uma compressão.
Passo 9
Agora, podemos desenhar e definir o estado plano de tensões para o ponto .
Pegando o desenho que tínhamos feito no final do passo 6 e adicionando a compressão na vertical de , obtemos nosso estado plano de tensões para :
Aí, a partir desse desenho, conseguimos definir as nossas tensões , e para o ponto :
Passo 10
FINALMENTE, chegamos ao último passo desse exercício.
Chegou a hora de calcular as tensões principais e a tensão de cisalhamento máxima no ponto .
Para tanto, começamos calculando e :
E em seguida, aplicamos que:
Para encontrarmos nossas respostas:
Resposta
Exercício Resolvido #3
Elaboração própria
O elemento mostrado na figura está rotacionado de 30° no sentido horário. Sabendo disso determine o valor das tensões principais e suas respectivas orientações.
Passo 1
Sabemos pela teoria quais fórmulas nos auxiliam nisso, sendo essas fórmulas dadas por
Que nos fornece o plano em que as tensões principais ocorrem
Que nos fornece a média das tensões
Que nos da o cisalhante máximo que o nosso elemento foi submetido
A ultima fórmula é dada por
Que de fato nos fornece o valor das tensões principais
Passo 2
Assim como temos as fórmulas, também temos os dados necessários para resolver a questão, que são dados por
Vamos resolvendo agora cada fórmula passo a passo
Primeiro vamos determinar a orientação em que ocorre as tensões principais
Isso é uma das orientações dos planos, mas também pode-se encontrar o outro subtraindo 90° do que encontramos
Passo 3
Agora que já sabemos qual é a orientação do plano, vamos determinar os valores necessários para encontrarmos os valores das tensões principais.
Sabemos que
Então
Também sabemos que
Logo
Passo 4
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 5
Agora devemos descobrir qual a orientação de cada plano. Com relação as tensões principais sabemos que
E sabemos que
Agora precisamos usar a fórmula
Substituiremos os nossos valores dado no elemento e escolheremos um dos ângulos para testar, assim saberemos a qual tensão cada ângulo pertence
Fazendo
Teremos que
então
E
Se já descobrimos a quem pertence um dos ângulos, com certeza o outro pertence a outa tensão.
Desenhando esse elemento teremos que
Logo
Resposta
Exercício Resolvido #4
Elaboração própria
Dado o elemento infinitesimal abaixo, determine as tensões principais, o cisalhante máximo e por fim a orientação dos planos em que essas tensões ocorrem.
Passo 1
Nessa questão sabemos que devemos determinar o valor das tensões principais, assim como o valor do cisalhante máximo.
Sabemos pela teoria quais fórmulas nos auxiliam nisso, sendo essas fórmulas dadas por
Que nos fornece o plano em que as tensões principais ocorrem
Que nos fornece a média das tensões
Que nos da o cisalhante máximo que o nosso elemento foi submetido
A ultima fórmula é dada por
Que de fato nos fornece o valor das tensões principais
Passo 2
Assim como temos as fórmulas, também temos os dados necessários para resolver a questão, que são dados por
Vamos resolvendo agora cada fórmula passo a passo
Primeiro vamos determinar a orientação em que ocorre as tensões principais
Isso é uma das orientações dos planos, mas também pode-se encontrar o outro subtraindo 90° do que encontramos
Passo 3
Agora que já sabemos qual é a orientação do plano, vamos determinar os valores necessários para encontrarmos os valores das tensões principais.
Sabemos que
Então
Também sabemos que
Logo
Passo 4
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 5
Agora devemos descobrir qual a orientação de cada plano. Com relação as tensões principais sabemos que
E sabemos que
Agora precisamos usar a fórmula
Substituiremos os nossos valores dado no elemento e escolheremos um dos ângulos para testar, assim saberemos a qual tensão cada ângulo pertence
Fazendo
Teremos que
Logo vemos que o ângulo que chamamos de 1 pertence a tensão 2, apenas para que fique homogêneo faremos que
E
Se já descobrimos a quem pertence um dos ângulos, com certeza o outro pertence a outa tensão.
Passo 6
Por fim, precisamos determinar a orientação do plano que ocorre o cisalhante máximo, para fazer isso, basta somar e subtrair 45° de algum dos ângulos que encontramos para as tensões principais
Usando
Teremos que os planos em que ocorrem a tensão cisalhante máxima são
Determinando assim o valor da orientação dos planos em que ocorre a tensão cisalhante máxima.
Resposta
Exercício Resolvido #5
Elaboração própria
Um porto sofre na ancoragem de navios esforços solicitantes que podem causar o seu colapso, principalmente quando ocorre encontro de grandes navios com a estrutura do porto. Em um dia foi constatado que a ancoragem de um navio exerceria sobre um porto uma força de 1000000 MN de força em uma área de 20 . Considere os seguintes dados.
A tensão cisalhante ao qual um elemento infinitesimal do material usado no porto é de 500Gpa. A estrutura do porto é extremamente forte para qualquer ação cisalhante, mas pode romper pela ação de um esforço normal que supere 600Gpa para o caso de compressão, ou 400GPa para o caso de tração. E não são considerados esforços na direção y do elemento infinitesimal.
Sabendo disso determine se o porto resistiria aos esforços provocados pela atracação desse navio.
Passo 1
Aqui vale perceber como ele apresenta alguns termos que já conhecemos.
Primeiro ele fala de uma força aplicada em uma determinada área do porto, como visualmente entendemos como se fosse uma pancada da lateral do navio com o porto, entendemos que essa solicitação se trata de um esforço normal de compressão, colocando em termo que conhecemos podemos escrever como
Como ele diz que esse esforço irá atuar sobre uma área de , podemos determinar, dessa maneira, a tensão normal no nosso porto, usando a fórmula
Passo 2
Também vale ressaltar o que ele diz sobre outros esforços. Ele afirma que não consideraremos tensões na direção y, logo
Também é dito no enunciado que a ação cisalhante no momento do impacto é de 500GPa, em termos que conhecemos
Por fim nos é dito que o porto pode suportar qualquer ação cisalhante (logo não precisamos nos preocupar com o cisalhante máximo) porém, para uma ação de 600GPa do esforço normal o nosso porto romperia por compressão, ou ainda a um esforço de tração ele romperia quando chegasse em 400GPa, com isso ele nos mostra que
Agora que já temos tudo que precisamos, vamos montar o nosso elemento infinitesimal.
Passo 3
Nosso elemento ficará
Como já sabemos, nesse estado o nosso elemento não está rompendo, pois já sabemos que o rompimento ocorre quando a tensão normal ultrapassa 600GPa, mas será que alguma tensão principal pode romper o nosso elemento? Vamos testar.
Passo 4
Nessa questão sabemos que devemos determinar o valor das tensões principais.
Sabemos pela teoria quais fórmulas nos auxiliam nisso, sendo essas fórmulas dadas por
Que nos fornece o plano em que as tensões principais ocorrem
Que nos fornece a média das tensões
Que nós dá o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais
Passo 5
Assim como temos as fórmulas, também temos os dados necessários para resolver a questão, que são dados por
Vamos resolvendo agora cada fórmula passo a passo
Primeiro vamos determinar a orientação em que ocorre as tensões principais
Isso é uma das orientações dos planos, mas também pode-se encontrar o outro subtraindo 90° do que encontramos
Passo 6
Agora que já sabemos qual é a orientação do plano, vamos determinar os valores necessários para encontrarmos os valores das tensões principais.
Sabemos que
Então
Também sabemos que
Logo
Passo 7
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 8
Agora precisamos pegar as nossas tensões principais e avaliar
Primeiro vamos analisar a compressão
Sabemos que na compressão a tensão admissível é de 600GPa, ou seja, quando comparamos com a nossa tensão principal de compressão, sabemos que o porto suportara a atracação desse navio.
Segundo vamos analisar a tração
Sabemos que na tração a tensão admissível é de 400GPa, ou seja, quando comparamos com a nossa tensão principal de tração, sabemos que o porto não suportara a movimentação do navio, tendo que tomar os devidos cuidados para que a atracação do navio não destrua o porto.
Mas já que sabemos que rompe na tração, em que sentido será esse rompimento?
Passo 9
Agora precisamos usar a fórmula
Substituiremos os nossos valores dado no elemento e escolheremos um dos ângulos para testar, assim saberemos a qual tensão cada ângulo pertence
Fazendo
Teremos que
Logo vemos que o ângulo que chamamos de 2 pertence a tensão 1, apenas para que fique homogêneo faremos que
E
Se já descobrimos a quem pertence um dos ângulos, com certeza o outro pertence a outa tensão.
Resposta
O porto não suportara pois rompera pelos esforços de tração que ocorrem na orientação de 46,43°
Exercício Resolvido #6
Elaboração própria
Uma força cisalhante age sobre uma área retangular de um foquete de 15 x 25m(área de ação da força). sabendo que a máxima tensão cisalhante suportada pelo foguete é de 50Mpa, e que a força aplicada é de 15000MN, determine se a estrutura dessa foguete resistiria a ação dessa força. Desprezar atuação de esforços normais na direção y e considere esforços normais na direção x de 30 Mpa. Também vale ressaltar que o foguete apresenta alta resistência a esforços normais.
Passo 1
Aqui vale perceber como ele apresenta alguns termos que já conhecemos.
Primeiro ele fala de uma força aplicada em uma determinada área do foguete, como essa força age lateralmente, sabemos que se trata de um esforço cortante.
Como ele diz que esse esforço irá atuar sobre uma área de , podemos determinar, dessa maneira, a tensão cisalhante no nosso foguete, usando a fórmula
Passo 2
Também vale ressaltar o que ele diz sobre outros esforços. Ele afirma que não consideraremos tensões na direção y, logo
Também é dito no enunciado que a ação normal no momento do impacto é de 30Mpa na direção x, em termos que conhecemos
Por fim nos é dito eu o foguete suporta 50Mpa de esforço cisalhante e possui altíssima resistência com relação a esfroços normais, ou seja, devemos nos preocupar com o valor do cisalhante máximo.
Agora que já temos tudo que precisamos, vamos montar o nosso elemento infinitesimal.
Passo 3
Nosso elemento infinitesimal será dado por
Como já sabemos, nesse estado o nosso elemento não está rompendo, pois já sabemos que o rompimento ocorre quando a tensão cisalhante ultrapassa 50MPa, mas será que o cislahante máximo ultrapassa esse valor?
Passo 4
Vamos diret ao que interessa, sabemos que o nosso cisalhante máximo é dado pelo valor de R, e sabemos que a fórmula que nos da R é
Substituindo os nossos dados temos que
Vemos então que o cisalhante máximo não ultrapassa o valor da tensão cisalahnte admissível.
Nesse caso, como sabemos que o material não rompe, não existe a necessidade de calcular a orientação do elemento, já que ele não representaria nada mais que uma rientação para o cisalhante máximo.
É importante lembrar que também não calculamos as tensões principais pelo fato de o material do foguete ser altamente resistente a tensões normais.
Resposta
O foguete resiste a ação da tensão cisalhante agindo nele já que máximo cislahante alcançado é de 42,72 Mpa quando a resistência máxima é de 50Mpa.
Exercício Resolvido #7
Elaboração própria
Um elemento infinitesimal de uma estrutura foi submetido ao carregamento mostrado abaixo. Sabendo que as tensões máximas suportada por essa peça são
Determine os fatores de segurança para cada uma das tensões (Normal e cisalhantes máximos que ocorrem nessa peça)
Passo 1
Nessa questão sabemos que devemos determinar o valor das tensões principais, assim como o valor do cisalhante máximo, pois ambos nos ajudaram no cálculo do fator de segurança
Sabemos pela teoria quais fórmulas nos auxiliam nisso, sendo essas fórmulas dadas por
Ou
Que nos fornece o fator de segurança para cada tensão
Que nos fornece a média das tensões
Que nos da o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais que serão usadas no nosso fator de segurança.
Passo 2
Assim como temos as fórmulas, também temos os dados necessários para resolver a questão, que são dados por
Vamos resolvendo agora cada fórmula passo a passo
Passo 3
Agora que já sabemos os dados, vamos determinar os valores necessários para encontrarmos os valores das tensões principais.
Sabemos que
Então
Também sabemos que
Logo
Passo 4
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 5
Sabemos que para determinarmos o fator de segurança devemos fazer a divisão entre a maior tensão suportada pela peça e a maior tensão aplicada a peça, dessa forma temos a fórmula
Ou
Sabemos que
E com relação as tensões máximas teremos que
Calculando os fatores de segurança, teremos
Logo o melhor fator de segurança que atende a peça é FS=1,27
Resposta
Exercício Resolvido #8
Elaboração própria
Um tubo de aço de paredes finas sofre a ação de um liquido pressurizado nas suas paredes internas. Sabendo que na pior situação de carregamento possível o elemento infinitesimal é o dado abaixo, determine se haverá segurança para a peça, ou seja, se os fatores de segurança para o normal e para o cisalhante na pior situação suportaram o carregamento dado.
Passo 1
Nessa questão sabemos que devemos determinar o valor das tensões principais, assim como o valor do cisalhante máximo, pois ambos nos ajudaram no cálculo do fator de segurança
Sabemos pela teoria quais fórmulas nos auxiliam nisso, sendo essas fórmulas dadas por
Ou
Que nos fornece o fator de segurança para cada tensão
Que nos fornece a média das tensões
Que nos da o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais que serão usadas no nosso fator de segurança.
Passo 2
Assim como temos as fórmulas, também temos os dados necessários para resolver a questão, que são dados por
Vamos resolvendo agora cada fórmula passo a passo
Passo 3
Agora que já sabemos os dados, vamos determinar os valores necessários para encontrarmos os valores das tensões principais.
Sabemos que
Então
Também sabemos que
Logo
Passo 4
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 5
Sabemos que para determinarmos o fator de segurança devemos fazer a divisão entre a maior tensão suportada pela peça e a maior tensão aplicada a peça, dessa forma temos a fórmula
Ou
Sabemos que
E com relação as tensões máximas teremos que
Calculando os fatores de segurança, teremos
Aqui vale ressaltar um ponto muito importante, a nossa peça não possui fator de segurança, pois ela rompe com o carregamento que estamos usando. Mas como percebemos isso?
Sempre que o nosso fator de segurança der menor que 1 significa que a nossa peça sofreu um rompimento, isso ocorre pois significa que a tensão máxima aplicada é maior que a tensão máxima admissível, logo ocorre o rompimento e independente do fator de segurança que usemos para o cisalhante a peça romperá pelo esforço normal.
Resposta
A nossa peça não possui fator de segurança pois ela rompe antes, isso se deve ao fato de termos calculado que
Ou seja, a tensão máxima suportada pela nossa peça é 35 Mpa, mas o que está aplicado nela é 38,6, ou seja, mesmo que o cisalhante suporte as tensões aplicadas nela, o normal não suportará, levando a peça ao rompimento.
Exercício Resolvido #9
Elaboração própria
O elemento infinitesimal abaixo sujeito a um determinado carregamento, apresentou o seguinte estado de tensões
Sabendo que o fator de segurança usado para essa peça tanto para a tensão Normal quanto para a tensão Cisalhante foi de 1,567, determine os valores de e
Passo 1
Nessa questão sabemos que devemos determinar o valor das tensões admissíveis, para isso vemos na fórmula abaixo que precisamos do valor do fator de segurança que é dado no enunciado e do valor das tensões máximas tanto cisalhante quanto normal, que já veremos como determinar. Sabemos que
Ou
Que nos fornece o fator de segurança para cada tensão
Que nos fornece a média das tensões
Que nos da o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais que serão usadas no nosso fator de segurança como as tensões máximas.
Passo 2
Assim como temos as fórmulas, também temos os dados necessários para resolver a questão, que são dados por
Vamos resolvendo agora cada fórmula passo a passo
Passo 3
Agora que já sabemos os dados, vamos determinar os valores necessários para encontrarmos os valores das tensões principais.
Sabemos que
Então
Também sabemos que
Logo
Passo 4
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 5
Olhando a nossa fórmula teremos que
Ou
Sabemos que
E com relação as tensões máximas teremos que
Substituindo na nossa fórmula teremos que
Fazendo isso teremos que
Resposta
Exercício Resolvido #10
Elaboração própria
A barra abaixo foi sujeita ao carregamento mostrado.
Sabendo que o raio da peça é de 30 mm e que o fator de segurança usado para essa peça para a tensão Normal foi de 1,47 e que para a tensão Cisalhante foi de 2,11 no pior caso de carregamento possível, determine os valores de e
Passo 1
Nessa questão sabemos que devemos determinar o valor das tensões admissíveis, para isso vemos na fórmula abaixo que precisamos do valor do fator de segurança que é dado no enunciado e do valor das tensões máximas tanto cisalhante quanto normal, que já veremos como determinar. Sabemos que
Ou
Que nos fornece o fator de segurança para cada tensão
Também sabemos que devemos determinar o estado de tensões da nossa peça, e com base nesse estado de tensões faremos
Que nos fornece a média das tensões
Que nos da o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais que serão usadas no nosso fator de segurança.
Passo 2
Olhando a nossa figura sabemos que devemos fazer primeiro um elemento infinitesimal na nossa peça, como mostra a figura
Sabemos que o que estará agindo no nosso elemento é um esforço de tração dado pela fórmula
Sabemos que
Substituindo teremos que
Olhando o nosso elemento infinitesimal, teremos que
Assim como temos as fórmulas, também temos os dados necessários para resolver a questão, que são dados por
Vamos resolvendo agora cada fórmula passo a passo
Passo 3
Agora que já sabemos os dados, vamos determinar os valores necessários para encontrarmos os valores das tensões principais.
Sabemos que
Então
Também sabemos que
Logo
Passo 4
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 5
Sabemos que para determinarmos o fator de segurança devemos fazer a divisão entre a maior tensão suportada pela peça e a maior tensão aplicada a peça, dessa forma temos a fórmula
Ou
Sabemos que
E com relação as tensões máximas teremos que
Substituindo teremos que
Fazendo isso teremos que