Transformações de Tensões
Produzido por Pablo RicardoTeoria
Introdução
No final do tópico anterior, nós definimos para um certo ponto de uma peça, o seguinte estado plano de tensões:
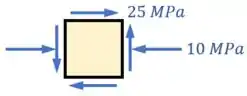
Ainda vimos como, dessa imagem, podemos definir nesse ponto as tensões normais e e a tensão cisalhante .
Agora...
Vamos dizer que um exercício da nossa prova pede que a gente determine as tensões nesse ponto, mas em um plano que forma um ângulo de com a horizontal, como na imagem abaixo:
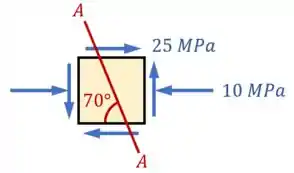
Como resolvemos esse exercício?
![]()
Transformação de Tensões
A solução para resolver esse exercício está em fazer uma transformação de tensões.
Essa transformação funciona assim:
1. Primeiro, precisamos ter eixos e definidos:
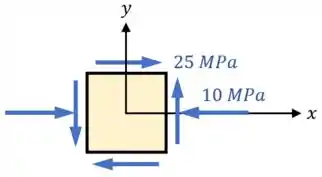
2. Depois, precisamos rotacionar esses eixos usando um ângulo (positivo no sentido anti-horário), obtendo assim novos eixos e :
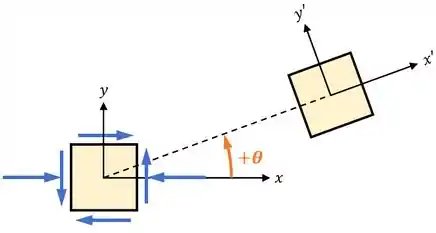
Sendo que aqui, o objetivo é fazer com que uma das faces do nosso elemento fique paralela ao plano .
Nesse caso, podemos fazer isso usando um ângulo ou usando um ângulo :
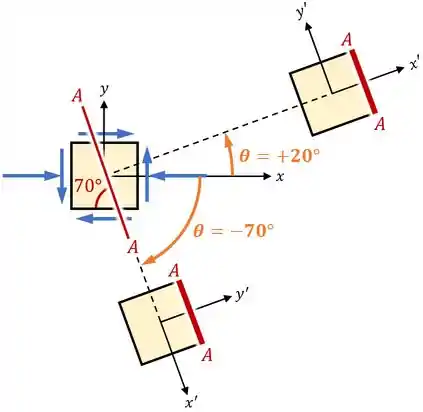
3. Em seguida, devemos calcular as tensões , e para o nosso elemento rotacionado:
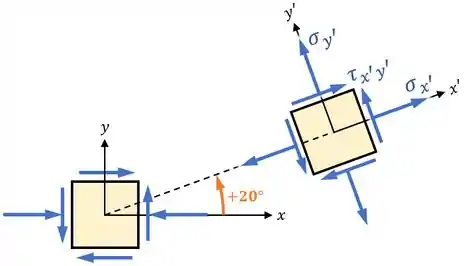
Aí, para calcular essas tensões, devemos usar as fórmulas:
Sendo que vale para essas fórmulas a dica:

E se alguma dessas fórmulas der um resultado negativo, isso significa que a tensão em questão tem um sentido contrário ao sentido convencional.
No nosso caso, por exemplo, substituindo , e , além de , vamos encontrar com essas fórmulas que:
E o desenho do nosso elemento rotacionado vai ficar assim:
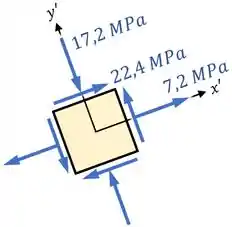
4. Por fim, vamos obter as tensões no plano observando uma face do nosso elemento que ficou paralela a esse plano:
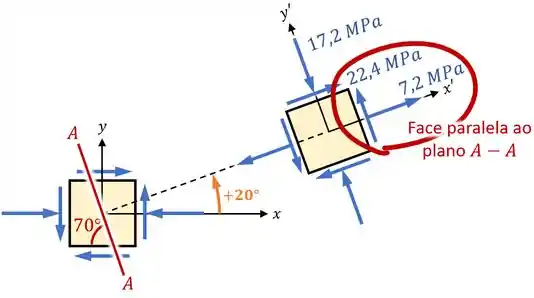
Nesse caso, vemos que as tensões no plano vão ser uma tensão normal de tração e uma tensão cisalhante !

Transformação de Tensões
Exercícios Resolvidos
Exercício Resolvido #1
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 333-9.10.
Determine o estado de tensão equivalente em um elemento, se ele estiver orientado a em sentido anti-horário em relação ao elemento mostrado. Use as equações de transformação de tensão.
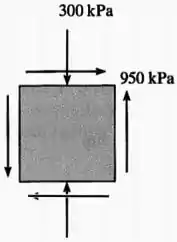
Passo 1
O que está acontecendo?
A imagem apresenta um estado plano de tensões em que:
- , uma vez que não há nenhuma tensão normal na horizontal;
- , com valor negativo uma vez que a tensão normal na vertical é de compressão;
- , com valor positivo uma vez que as setas da tensão cisalhantes está apontando para o 1° e 3° quadrante:
E o que é que o exercício quer?
Ele quer que a gente determine o estado de tensão , e nesse elemento caso os seus eixos sejam rotacionados por um ângulo em sentido anti-horário ():
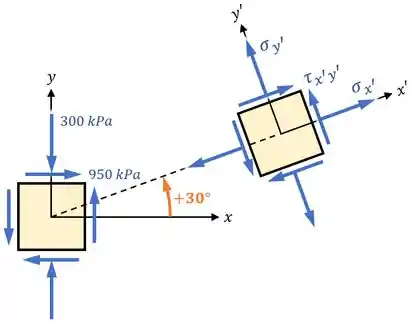
Para tanto, ele quer que a gente use as equações de transformação de tensões:
Então, para resolver esse exercício...
O primeiro passo é fazer o desenho que acabamos de fazer do elemento rotacionado.
O segundo é aplicar as equações de transformação de tensões.
E o terceiro é colocar os resultados encontrados no desenho do elemento rotacionado.
Com uma observação:
Caso o exercício pedisse somente as tensões , e , esse terceiro passo poderia ser pulado.
Mas como ele pediu que a gente determine o “estado de tensões equivalente”, imagina-se que ele quer que a gente faça um desenho desse estado de tensões.
Sendo que no geral, é sempre bom fazer esse desenho final mesmo. 😉
Passo 2
Então vamos lá!
Já fizemos no passo anterior um desenho do nosso elemento rotacionado, o que nos ajudou a identificar corretamente o ângulo .
Agora, é só uma questão de aplicar as fórmulas da transformação de tensões:
Substituindo nessas equações os valores:
- ;
- ;
- ;
- & ,
Elas vão ficar assim:
Aí, calculando essas expressões, vamos encontrar que:
Passo 3
No passo anterior, já encontramos as respostas do nosso exercício, mas para complementar a nossa solução, podemos desenhar essas tensões no nosso elemento rotacionado.
Para tanto, podemos perceber que:
- As tensões e , por serem positivas, vão ter seus sentidos convencionais no desenho.
- Já a tensão , negativa, vai ser representada no desenho somente com sua intensidade de , mas com um sentido oposto do convencional, ou seja, com o sentido de compressão.
Dessa forma, o estado plano de tensões para o nosso elemento rotacionado fica assim:
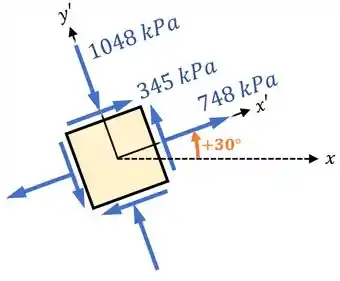
E pronto!
Está resolvido o exercício.
Resposta
Exercício Resolvido #2
Questão 1 da 2ª Prova Mecânica dos Materiais 1 - 2012.2 - Professores Alex e Éder - UnB. (Adaptado de Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 456-7.29.)
Para o estado de tensão mostrado, determine: o valor de para o qual a tensão de cisalhamento no plano da cola seja zero e a tensão normal correspondente.
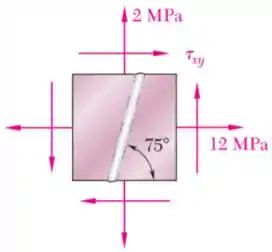
Passo 1
O que está acontecendo?
O elemento da figura possui um estado plano de tensões com:
- ;
- ;
- & desconhecido.
E o que é que o exercício quer saber?
Na letra , ele quer saber qual deve ser o valor de para que a tensão de cisalhamento no plano da cola seja zero.
Então devemos tentar descrever a tensão de cisalhamento no plano da cola!
Fazendo isso, vamos poder igualar essa tensão a zero e descobrir qual é o valor de correspondente.
Já na letra , o exercício quer saber qual vai ser a tensão normal no plano da cola tendo em mente esse caso proposto no item .
Então, para resolver o exercício...
Temos que fazer uma transformação de tensões nesse elemento com o objetivo de descrever a tensão de cisalhamento no plano da cola.
Isso envolve:
1. Definir um ângulo (positivo se for sentido anti-horário) de rotação que faça com que uma face do nosso elemento fique paralela ao plano da cola.
2. Aplicar a fórmula da transformação de tensões para a tensão de cisalhamento, usando esse ângulo definido no passo anterior:
& 3. Igualar essa fórmula a zero, de tal forma que a gente possa isolar e descobrir qual deve ser seu valor.
Depois que isso tiver sido feito, vamos poder seguir para o item , em que devemos:
1. Identificar se a tensão normal no plano da cola vai corresponder à tensão ou do elemento rotacionado.
(Isso depende do ângulo que tivermos escolhido.)
& 2. Aplicar a fórmula correspondente de transformação de tensões para a tensão normal:
Passo 2
Então vamos começar definindo a rotação do nosso elemento.
Uma opção é rotacionar ele com um ângulo , fazendo com que sua face direita fique paralela ao plano da cola:
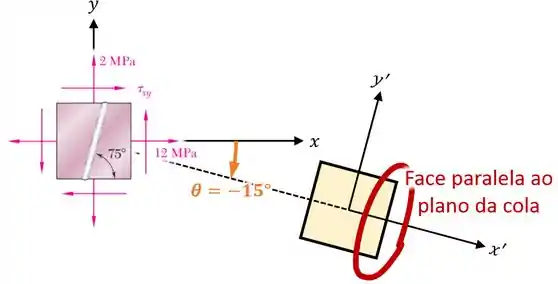
E assim está definida a nossa rotação!
Passo 3
Agora que já definimos a rotação , podemos aplicar a fórmula da transformação de tensões para a tensão de cisalhamento:
Aí, substituindo , & , essa fórmula fica assim:
Daí que, calculando tudo isso, encontramos que:
Passo 4
Descrita a tensão de cisalhamento no plano da cola, podemos agora igualá-la a zero para encontrar a tensão de cisalhamento original necessária para satisfazer essa condição.
Fazendo isso, vamos ter:
Isolando , encontramos que:
O que dá:
Que é a nossa resposta para a letra .
Passo 5
Agora, para a letra , podemos olhar de novo para a rotação que definimos:
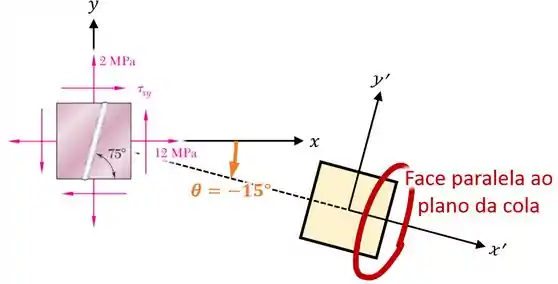
Olhando para essa imagem, vemos que:
A tensão normal que vai atuar no plano da cola deve ser a mesma tensão normal que atua na face paralela ao plano da cola, que é a tensão na direção .
Dessa forma, temos que a tensão normal no plano da cola vai ser dada pela fórmula:
Daí que, substituindo nessa fórmula , , & , ela fica assim:
Calculando tudo isso, encontramos que:
Ou seja, a tensão normal no plano da cola é uma tensão de tração de .
Resposta
Exercício Resolvido #3
Elaboração própria
Determine o estado de tensões do elemento infinitesimal dado abaixo quando analisamos um plano orientado a 37° no sentido anti-horário.
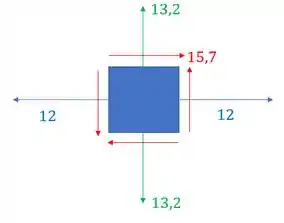
Passo 1
Aqui é importante entender o que está ocorrendo, a figura abaixo demonstra o que o enunciado fala
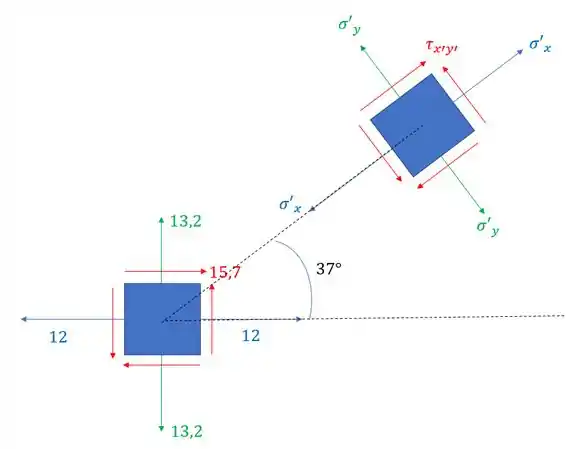
Sabemos então que se trata de uma simples transformação de tensão, que sabemos que devemos usar as seguintes fórmulas para determinar o estado de tensões do elemento que está a 37°
Passo 2
Agora que já sabemos qual o problema e quais fórmulas devemos usar, vamos ir encontrando cada valor do nosso elemento quando orientado a 37°
Sabemos que
Substituindo os valores em cada uma das equações teremos que
Passo 3
Redesenhando o elemento no novo estado de tensões teremos que
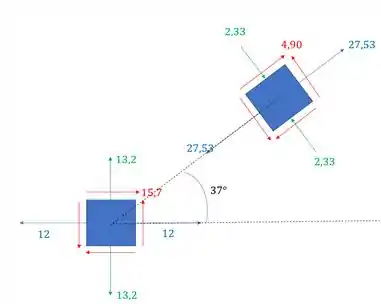
Resposta
Exercício Resolvido #4
Elaboração própria
Determine o estado de tensões de um elemento infinitesimal orientado de 79° no sentido horário.
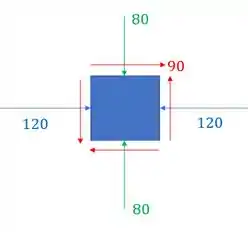
Passo 1
Aqui é importante entender o que está ocorrendo, a figura abaixo demonstra o que o enunciado fala
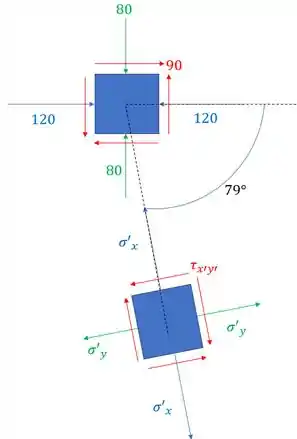
Sabemos então que se trata de uma simples transformação de tensão, que sabemos que devemos usar as seguintes fórmulas para determinar o estado de tensões do elemento que está a 79°. Aqui vale ressaltar um ponto muito importante, todos os ângulos em transformação de tensões que giram no sentido horário entram na fórmula com sinal negativo.
Passo 2
Agora que já sabemos qual o problema e quais fórmulas devemos usar, vamos ir encontrando cada valor do nosso elemento quando orientado a 79°
Sabemos que
Substituindo os valores em cada uma das equações teremos que
Passo 3
Redesenhando o elemento no novo estado de tensões teremos que

Resposta
Exercício Resolvido #5
Elaboração própria
Uma barra de ferro foi remendada segundo o ângulo mostrado na figura. Sabendo que ela será submetida aos esforços mostrados determine quais tensões apareceram no plano da emenda.
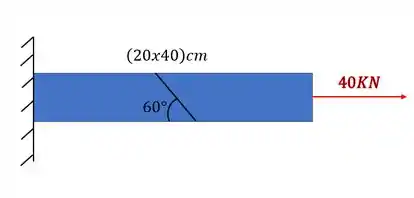
Passo 1
Vamos representar o nosso elemento infinitesimal de forma a trocar a nossa barra por um elemento que simbolize a ação do carregamento. Dessa forma teremos que o nosso elemento infinitesimal será
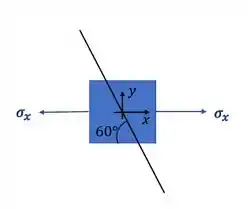
Também devemos rotacionar o nosso elemento de forma que a parede lateral do quadrado fique paralela a emenda da barra, que é exatamente o nosso plano orientado a 60°, logo as possíveis posições do nosso elemento serão
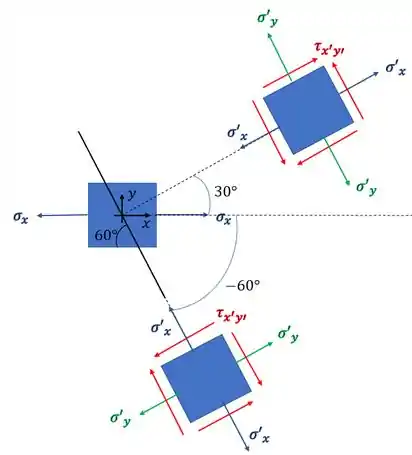
Passo 2
Sabemos também que as fórmulas que nos permitem calcular as tensões nesse plano são dadas por
Em que o nosso elemento apresenta apenas e .
Passo 3
Olhando novamente a nossa barra, teremos que
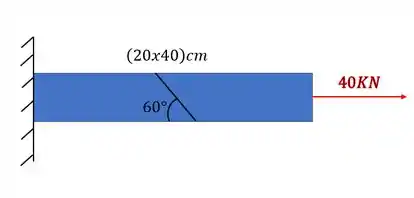
Sabemos que
Em que
Substituindo teremos que
Agora que temos todos os valores, vamos substituir na nossa fórmula.
Passo 4
E vamos testar para dois ângulos, primeiro com e depois com
Passo 5
Primeiro com
Primeiro com
Redesenhando o nosso elemento com as tensões encontradas teremos o seguinte estado de tensões
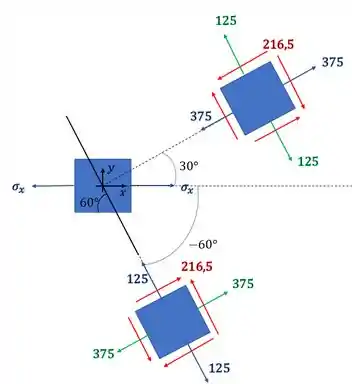
Marcando no desenho o plano que nos interessa teremos que
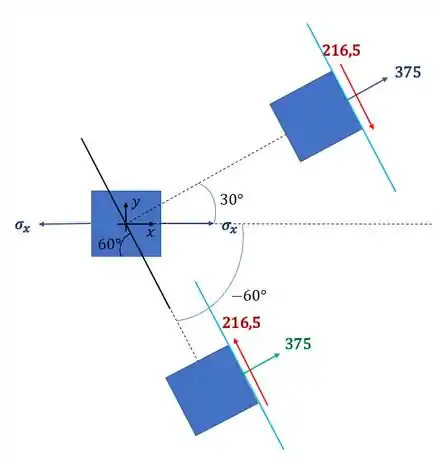
Podemos ver que a tensão que age no plano da emenda é dada pelas tensões que agem no plano azul do nosso desenho, assim podemos dizer que
Resposta
Exercício Resolvido #6
Elaboração própria
um garoto sofreu um acidente em que o osso do seu braço teve quer ser colado segundo o ângulo mostrado na figura. Sabendo que esse garoto foi jogar bola e sofreu uma entrada em que o osso do seu braço foi submetido aos esforços mostrados na figura. Sabendo que a tensão máxima cisalhante suportada no plano de rompimento é de 50KPa, determine se a entrada sofrida pelo garoto será suficiente para causar novamente o rompimento do seu osso.
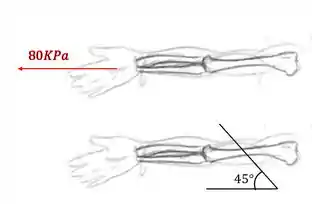
Passo 1
Vamos representar o nosso elemento infinitesimal de forma a trocar o nosso braço por um elemento que simbolize a ação da entrada no jogo de futebol. Dessa forma teremos que o nosso elemento infinitesimal será
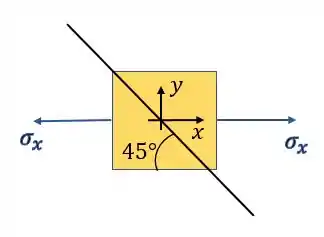
Também devemos rotacionar o nosso elemento de forma que a parede lateral do quadrado fique paralela a colagem do osso, que é exatamente o nosso plano orientado a 45°, logo as possíveis posições do nosso elemento serão
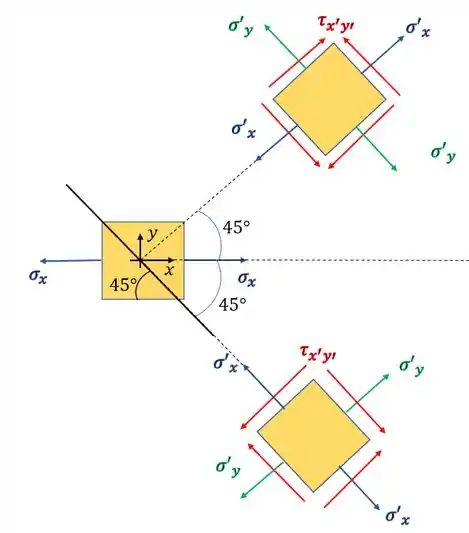
Passo 2
Sabemos também que as fórmulas que nos permitem calcular as tensões nesse plano são dadas por
Em que o nosso elemento apresenta apenas e .
Passo 3
Olhando novamente o nosso braço, teremos que
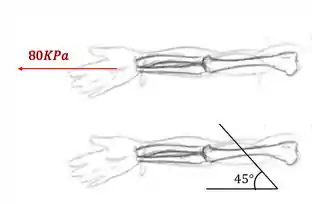
Sabemos que
Agora que temos todos os valores, vamos substituir na nossa fórmula.
Passo 4
E vamos testar para um único ângulo de
Passo 5
Com
Redesenhando o nosso elemento com as tensões encontradas teremos o seguinte estado de tensões
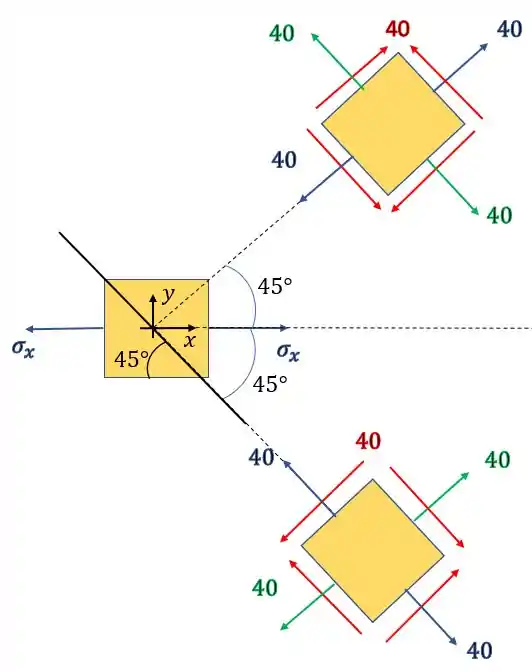
Marcando no desenho o plano que nos interessa teremos que
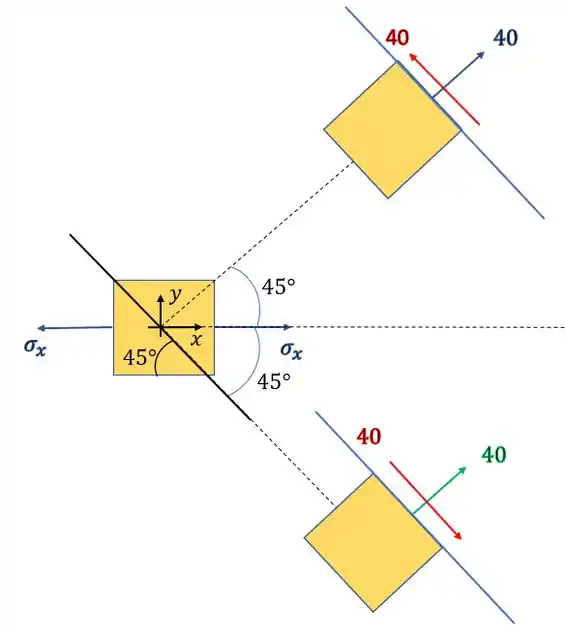
Podemos ver que a tensão que age no plano da emenda é dada pelas tensões que agem no plano azul do nosso desenho, assim podemos dizer que
Mas o objetivo da questão era saber se a entrada sofrida pelo garoto seria o suficiente para que novamente o braço do menino voltasse a quebrar-se.
Como foi dito no enunciado a resistência no plano era de 50KPa, como a tensão cisalhante no plano é de 40KPa podemos afirmar que não ocorrerá ruptura no braço do menino.
Resposta
A entrada sofrida pelo garoto não será suficiente para romper novamente o osso de seu braço, isso pois a resistência no plano de emenda é de 50KPa, enquanto que a máxima tensão cisalhante ocorrida no plano é de 40KPa.
Exercício Resolvido #7
Elaboração própria
Abaixo é dado um elemento infinitesimal sujeito aos esforços mostrados. Usando seus conhecimentos de transformação de tensões, mostre que as tensões no plano a 75° no sentido anti-horário são as mesmas das do plano a 15° no sentido horário.
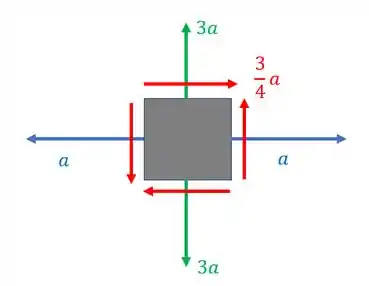
Passo 1
Aqui é importante entender o que está ocorrendo, a figura abaixo demonstra o que o enunciado fala
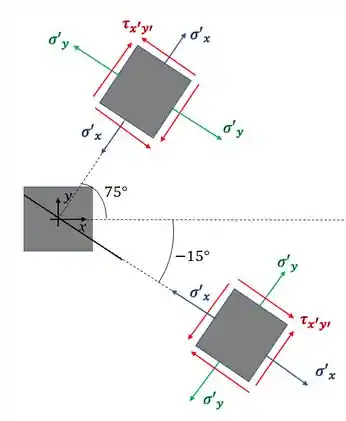
Sabemos então que se trata de uma simples transformação de tensão, que sabemos que devemos usar as seguintes fórmulas para determinar o estado de tensões do elemento que está a 75° e a 15°
Passo 2
Agora que já sabemos qual o problema e quais fórmulas devemos usar, vamos ir encontrando cada valor do nosso elemento quando orientado a 75° e a 15°
Sabemos que
Substituindo os valores em cada uma das equações teremos que
Primeiro usando
Agora usando
Passo 3
Redesenhando o elemento no novo estado de tensões teremos que
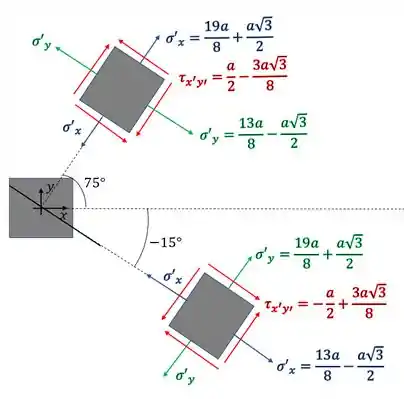
Agora pelo desenho podemos ver que esforços na mesma direção possuem o mesmo valor, logo temos que
Resposta
Exercício Resolvido #8
Elaboração própria
O elemento infinitesimal abaixo está sujeito aos esforços mostrados. Determine quanto deve valer a tensão no eixo x para que a tensão em x e em y sejam iguais quando o elemento estiver rotacionado de 22,5° no sentido anti-hor��rio.
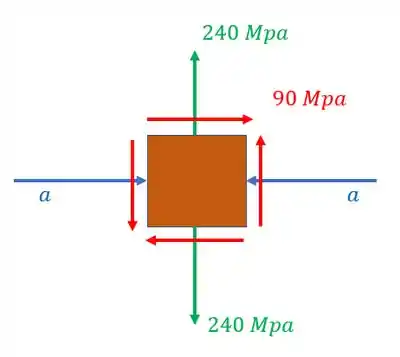
Passo 1
Aqui é importante entender o que está ocorrendo
Sabemos que devemos garantir que as tensões no estado transformado sejam iguais, como sabemos que as fórmulas são
Basta que igualemos essas tensões para sabermos o que deveremos fazer, fazendo isso teremos que
Cortando a média das tensões teremos que
Isolando teremos que
Como queremos isolar o valor de x teremos que
Passo 2
Agora que já temos a nossa fórmula basta que substituamos os valores, com isso teremos que
Vamos substituir na equação que encontramos antes
Agora vamos testar para ver se de fato fizemos correto.
Passo 3
Usando a nossa fórmula teremos que
Logo de fato fizemos o cálculo correto e de fato na orientação 22,5° temos que a tensão no eixo x seria
Que quando orientado terá
Resposta
Exercício Resolvido #9
Elaboração própria
O elemento infinitesimal abaixo está sujeito aos esforços mostrados. Determine quanto deve valer a tensão cisalhante para que a tensão em x seja o dobro da tensão em y quando o elemento estiver rotacionado de 45°no sentido anti-horário.
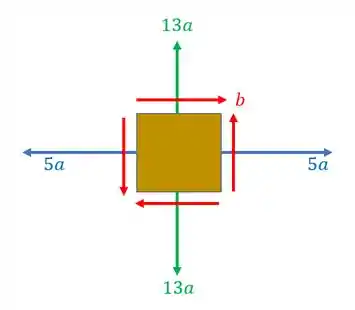
Passo 1
Aqui é importante entender o que está ocorrendo
Sabemos que devemos garantir que as tensões no estado transformado e no eixo x sejam iguais ao dobro das tensões no eixo y, como sabemos que as fórmulas são
Basta fazermos a igualdade que foi mencionada afim de que essas tensões sejam iguais, para isso faremos
Isolando tudo em um lado teremos que
Isolando as tensões teremos que
Com isso teremos que a fórmula será
Passo 2
Agora que já temos a nossa fórmula basta que substituamos os valores, com isso teremos que
Vamos substituir na equação que encontramos antes
Logo teremos que
Agora vamos testar para ver se de fato fizemos correto.
Passo 3
Usando a nossa fórmula teremos que
Se achamos que a tensão em x é de , sabemos que para estar correto a tensão em y deverá ser de , vamos testar então
Logo de fato a conta que fizemos está correta, como o objetivo era determinar o valor do cisalhante, teremos que o nosso cisalhante deverá valer
Para que a nossa tensão no eixo x seja o dobro da tensão no eixo y quando girarmos o nosso elemento em 45° no sentido anti-horário.
Resposta
Exercício Resolvido #10
Elaboração própria
Dado o elemento infinitesimal abaixo, determine o ângulo em que a tensão no eixo x será o quíntuplo da tensão cisalhante somado a tensão no eixo y.
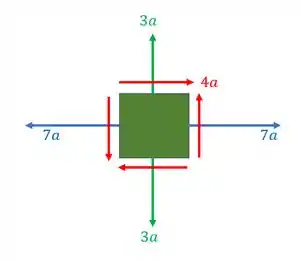
Passo 1
Aqui é importante entender o que está ocorrendo
Sabemos que devemos garantir que as tensões no estado transformado e no eixo x sejam iguais ao quíntuplo das tensões cisalhantes somado a tensão no eixo y, como sabemos que as fórmulas são
Passo 2
Basta fazermos a igualdade que foi mencionada afim de que essas tensões sejam iguais, para isso faremos
Cortando as médias de ambos os lados teremos que
Isolando tudo de um lado teremos que
Além da fórmula sabemos que
Substituindo na nossa equação teremos que
Isolando a tangente teremos que
Isolando o valor dos ângulos teremos que
Agora que já determinamos o nosso ângulo, vamos testar na nossa fórmula para vermos se fizemos os cálculos corretamente.
Passo 3
Usando a nossa fórmula teremos que
Vamos testar os valores na nossa fórmula para sabermos se os cálculos estão ok
Como o valor que calculamos foi
Vemos que a pequena diferença acontece pelas aproximações que fizemos, como conseguimos provar que de fato os nossos cálculos estão corretos, conseguimos determinar o ângulo que satisfaz a nossa equação que nesse caso é