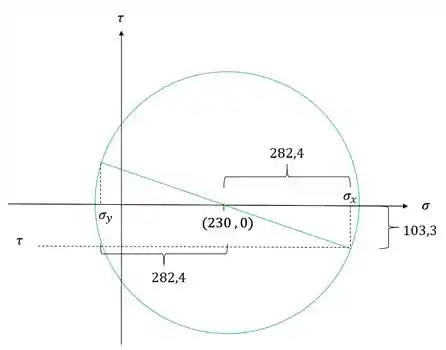
Círculo de Mohr
Produzido por Pablo RicardoTeoria
O Círculo de Mohr é uma método gráfico para a transformação de tensões e determinação das tensões principais. Ele é bastante cobrado em provas! Então bora aprender tudo sobre ele?! 😉
Como Desenhar o Círculo de Mohr: Passo a Passo
Então... Como é que a gente desenha o Círculo de Mohr!? A gente vai aprender na prática, fazendo um exemplo passo a passo!
Passo 1: Definir as Tensões
Nesse passo a gente precisa de um quadrado de referência. Nele consideramos um ponto do material onde analisamos as tensões que ocorrem em todos os planos. Assim:
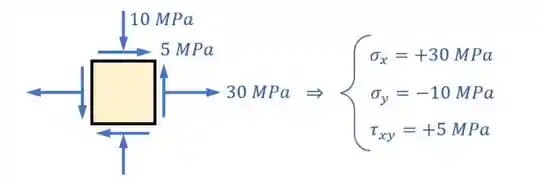
No tópico Esforços Combinados e o Estado Plano de Tensões a gente ensina como fazer isso passo a passo! Aqui eu vou falar mais rapidinho, mas qualquer coisa é só dar uma revisada no link acima! 😉
Passo 2: Definir os Eixos
Definido o seu estado de tensões, você pode agora desenhar dois eixos! Vamos colocar o eixo
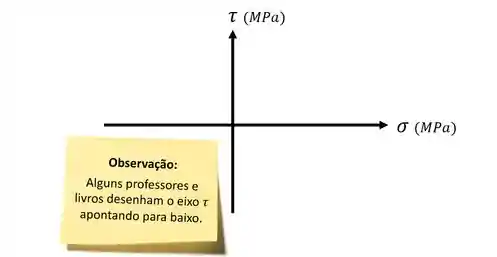
O
Passo 3: Definir os Pontos do Centro e das Tensões do Eixo x
O primeiro ponto vai ser o centro do seu círculo, definido como:
E o segundo ponto vai representar as tensões no eixo x do seu estado de tensões e é definido como:
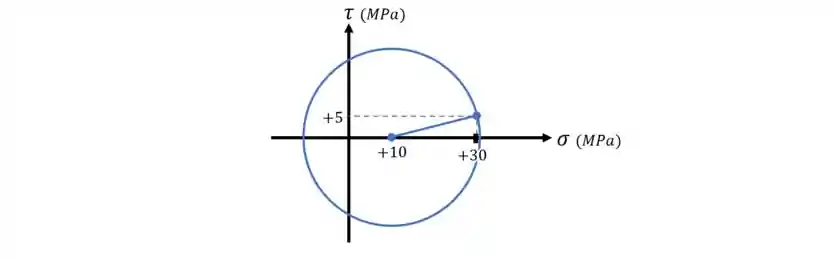
Agora a gente vai plotar esses pontos no gráfico e ligar eles, assim:
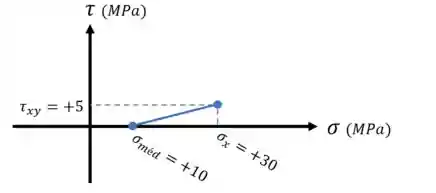
Passo 4: Desenhar o Gráfico
Essa é a parte mais simples! Você vai pegar o seu compasso, colocar a agulha no centro do círculo e o grafite no ponto de tensões do eixo x. Depois é só girar o compasso formando uma circunferência!
Vai ficar assim:
Como Usar o Círculo de Mohr
Agora que sabemos como desenhar o círculo de Mohr temos um mundo de possibilidades! Bora aprender que informações iradosas a gente pode tirar dele?!
Se liga nesse vídeo então! 👇
Tensão Normal no Eixo y
Vimos lá em cima, que a reta que desenhamos indica a tensão normal
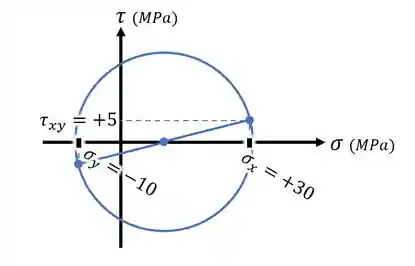
Rotação do Elemento
Caso a gente queria utilizar o Círculo de Mohr para realizar uma transformação de tensões, nós podemos rotacionar o elemento. Digamos que precisamos descobrir as tensões no nosso elemento quando inclinado por um ângulo
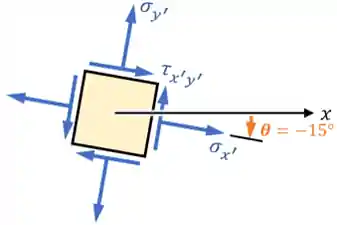
Nesse caso, o que precisamos fazer é rotacionar a nossa reta do círculo por um ângulo
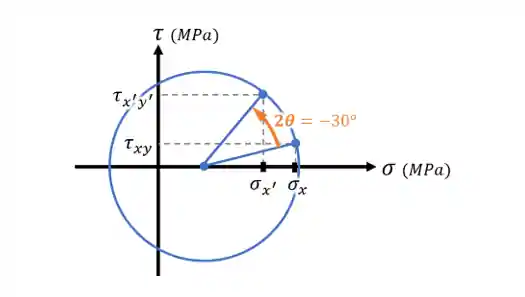
Cálculo das Tensões no Elemento Rotacionado
Feita a rotação no Círculo de Mohr, temos duas formas de encontrar os valores das tensões
- A primeira, caso estejamos utilizando um papel quadriculado, é utilizar o quadriculado para medir essas tensões;
- A segunda é utilizar trigonometria (seno, cosseno, tangente e até um pouco de pitágoras) para calcular essas tensões.
Tensões Principais
O Círculo de Mohr também pode ser utilizado para encontrar as tensões principais em um elemento.
As tensões principais não são aquelas que acontecem quando a tensão cisalhante é nula. Olhando pro círculo, vemos que dá para rotacionar a reta que desenhamos até que ela fique na horizontal, fazendo com que a tensão cisalhante
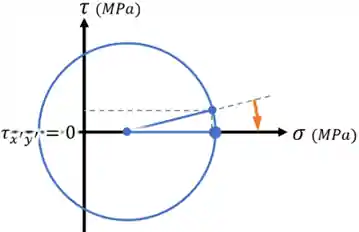
Então, as tensões que aparecem nesse momento vão ser as nossas tensões principais
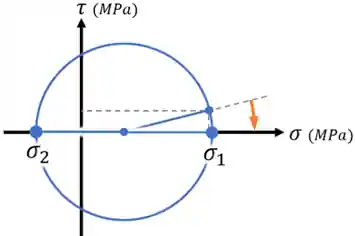
Para calcular as tensões principais usando o Círculo de Mohr, podemos calcular o raio R do círculo usando Pitágoras:
Como mostra a imagem abaixo:
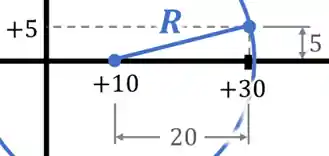
Sendo que esse raio R é o mesmo “R” que calculávamos quando estudamos as tensões principais.
Assim, podemos calcular as tensões principais fazendo:
Orientação das Tensões Principais
E se quisermos encontrar as orientações
Aí, podemos nos lembrar:
- Que uma rotação
no elemento corresponde a uma rotação no Círculo de Mohr; - E que enquanto que
é positivo no sentido anti-horário no elemento, no Círculo de Mohr os ângulos são positivos no sentido horário.
Lembrando disso e usando um transferidor, conseguimos medir os ângulos
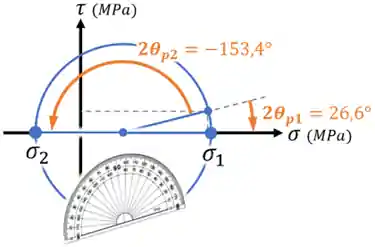
Tensão de Cisalhamento Máxima
Se quisermos saber a tensão de cisalhamento máxima no nosso elemento, só precisamos rotacionar ele até fazer essas tensões aparecerem:
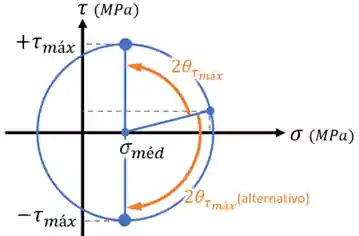
Fazendo isso, percebemos:
- Como
é igual ao raio do nosso círculo e pode ser calculado assim:
- Como as tensões normais e assumem o valor quando a tensão de cisalhamento é máxima.
Para encontrarmos o valor desses ângulos
- Usar um transferidor;
- Usar seno/cosseno/tangente e as funções arcsen, arccos ou arctg da nossa calculadora para calcular algum ângulo que nos auxilie a encontrar esses ângulos.
Agora vamos praticar com exercícios?!
Tensão de Cisalhamento Máxima
Exercícios Resolvidos
Exercício Resolvido #1
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 349-9.78.
Obtenha o círculo de Mohr que descreve cada um dos seguintes estados de tensão:
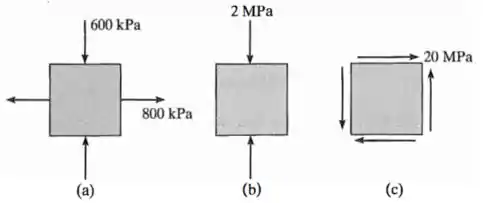
Passo 1
O exercício quer que a gente desenhe o Círculo de Mohr para cada um dos estados de tensão mostrados.
Então lembra aí!
Para desenhar um Círculo de Mohr, devemos começar definindo as tensões , e do estado de tensões.
Feito isso, vamos poder calcular a tensão normal média:
...para, em seguida, marcarmos os pontos e em um gráfico .
Aí, usando o primeiro ponto como o centro do círculo, podemos abrir um compasso até o segundo ponto e desenha o Círculo de Mohr!
Passo 2
Então vamos lá!
Começando pelo item :
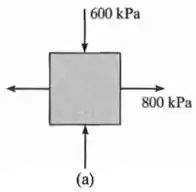
Nele, temos uma tração na horizontal de , uma compressão na vertical de , e nenhuma tensão de cisalhamento
Dessa forma, vamos ter que:
Agora, podemos calcular :
Desenhar os eixos e :
E em seguida marcar entre esses eixos os pontos e , ligar esses pontos e usá-los para desenhar nosso círculo:
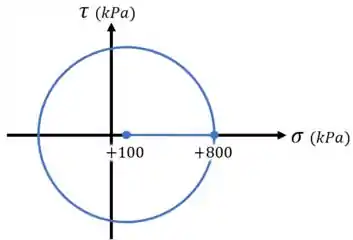
E pronto!
Item resolvido.
Passo 3
Agora, para o item :

Nós vamos ter:
Dessa forma, vai ser:
Aí, marcando esse ponto e o ponto em um gráfico , ligando esses pontos e usando eles para desenhar um círculo, vamos ter o desenho:
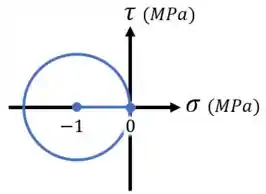
Que é a resposta do item .
Passo 4
E para o item :
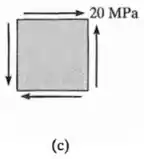
Temos:
De tal forma que:
Aí, marcando esse ponto e o ponto em um gráfico , ligando esses pontos e usando eles para desenhar um círculo, vamos ter:
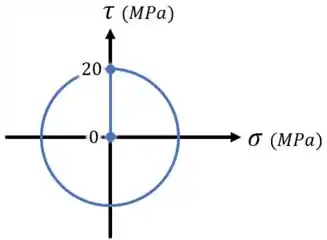
Que é a resposta do item .
E assim finalizamos o exercício!
Resposta
Exercício Resolvido #2
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 349-9.72. (Adaptado)
Utilizando o círculo de Mohr, determine as tensões principais e a tensão de cisalhamento máxima no plano e a tensão normal média. Especifique a orientação do elemento em cada caso.
Passo 1
O que está acontecendo?
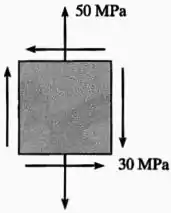
O exercício nos forneceu pela imagem um estado plano de tensões onde:
- Não existe tensão normal na horizontal, de tal forma que:
- Existe na vertical uma tração de , de tal forma que:
- E existe uma tensão de cisalhamento de , mas que está no sentido oposto de sua convenção usual, de tal forma que:
E o que é que ele quer?
Ele quer que a gente use o círculo de Mohr para determinar:
as tensões principais e e suas orientações e ;
& a tensão de cisalhamento máxima no plano , a tensão normal média que acompanha essa tensão de cisalhamento máxima e as orientações que causam essas tensões.
Então, para resolver esse exercício, vamos:
1. Calcular e utilizar esse ponto e o ponto para desenhar o Círculo de Mohr para esse estado de tensões.
2. Usar o teorema de Pitágoras para encontrar o raio do círculo de Mohr e, em seguida, calcular as tensões principais nele.
3. Usar seno, cosseno ou tangente no círculo de Mohr e a função , ou na calculadora para descobrir o valor dos ângulos e .
4. Aplicar e aproveitar o valor já calculado de para definir as tensões pedidas pelo item .
& 5. Aproveitar o ângulo encontrado no terceiro passo para estudar os ângulos no círculo de Mohr e reconhecer os ângulos que levam o elemento à orientação em que a tensão de cisalhamento é máxima.
Passo 2
Então vamos lá!
Como já definimos no passo anterior as tensões , e no nosso estado plano de tensões, já podemos agora calcular :
Desenhar os eixos e :
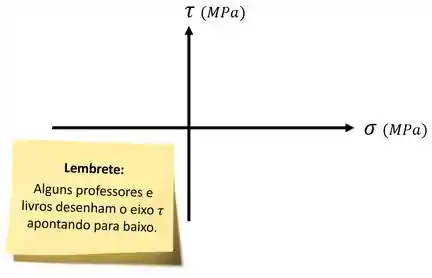
E em seguida marcar entre esses eixos os pontos:
- ;
- & ,
...para depois ligar esses pontos e usá-los para desenhar nosso círculo:
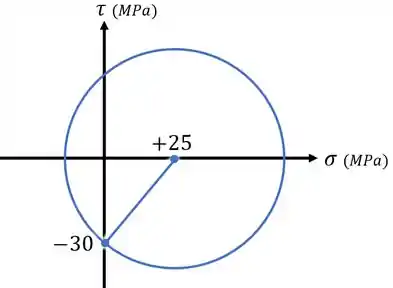
E pronto!
Nosso círculo de Mohr está desenhado.
Agora, devemos usar ele para determinar o que foi pedido pelo exercício.
Passo 3
Primeiro, para descobrirmos as tensões principais usando o círculo de Mohr, precisamos calcular o raio do círculo.
Para tanto, podemos olhar para o desenho do círculo um pouco acima e utilizar o teorema de Pitágoras:
Calculando , encontramos que:
Com isso, podemos calcular as nossas tensões principais e :
Substituindo e , encontramos que:
Passo 4
Agora, vamos observar no nosso círculo de Mohr os ângulos que fazem essas tensões principais aparecerem:
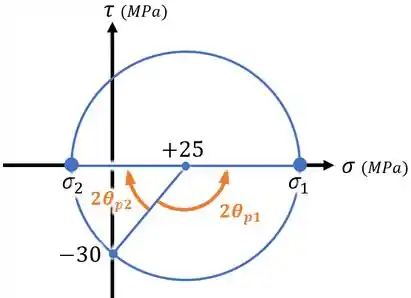
Sendo que aqui, precisamos nos lembrar que:
- Lá no estado de tensões, um ângulo é positivo no sentido anti-horário;
- Então, como desenhamos no nosso círculo de Mohr o eixo apontando para cima, os ângulos no círculo vão ser positivos no sentido horário.
Assim, concluímos que é um ângulo negativo, por estar no sentido anti-horário no círculo de Mohr, enquanto que é um ângulo positivo.
Tendo isso em mente, podemos calcular o valor desses ângulos.
Uma forma de fazer isso é vendo que:
Aí, usando a função da nossa calculadora, e se lembrando de verificar se a calculadora está fornecendo resultados em graus, encontramos que:
O que significa que:
E aí agora, nós sabemos que quando conhecemos um ângulo (nesse caso ), o outro (nesse caso ) pode ser encontrado adicionando ou subtraindo do primeiro.
Dessa forma, temos que:
O que dá:
E assim terminamos o item !
Passo 5
Agora, para resolver o item , nós podemos aproveitar o que calculamos para o item .
Sabemos que a tensão de cisalhamento máxima no plano é sempre igual ao raio do círculo de Mohr, então temos que:
E lá no passo 3, calculamos que , então:
Além disso, sabemos que quando a tensão de cisalhamento no plano é máxima, as tensões normais assumem o valor médio , que já calculamos no passo 2 como:
E assim, em alguns segundos, encontramos as tensões pedidas pelo item .
Passo 6
Mas ainda precisamos encontrar as orientações do elemento que fazem aparecer essas tensões de cisalhamento máximas e normais médias do item .
Para tanto, vamos olhar para os possíveis ângulos no círculo de Mohr que causam essas tensões:
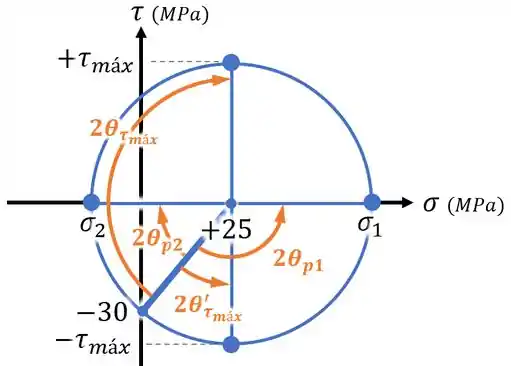
A primeira opção, , está no sentido horário no círculo de Mohr e é portanto positiva (seria negativa caso tivéssemos usado desde o começo um eixo apontando para baixo).
Olhando para o círculo, ainda vemos que ela é maior que o ângulo .
Então, temos que:
Realizando essa soma e dividindo por 2, encontramos que:
Já a segunda opção, :
- é negativa;
- & é “maior” que o ângulo
E no passo passo 4, encontramos que , o que significa que .
Ou seja:
Finalmente, dividindo isso por 2, temos:
Ou seja, o ângulo que podemos usar para rotacionar o nosso elemento e fazer aparecer a tensão de cisalhamento pode ser um ângulo de ou um ângulo de .
E assim finalizamos o nosso exercício!
Resposta
Exercício Resolvido #3
Questão 2 da 2ª Prova Mecânica dos Materiais 1 - 2015.1 - Professores Alex e Éder - UnB.
Para o estado de tensão mostrado na figura, determine, usando Círculo de Mohr, a tensão normal e a tensão de cisalhamento atuantes no plano .
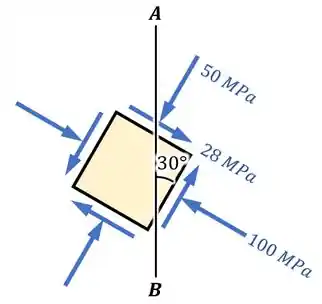
Passo 1
O que está acontendo?
O exercício nos forneceu um estado plano de tensões, para o qual podemos definir eixos e :
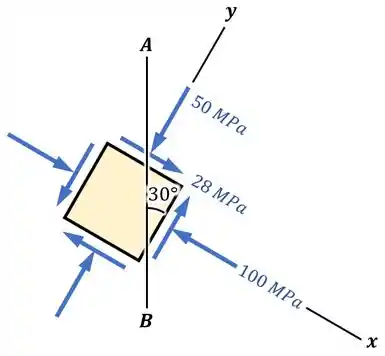
Fazendo isso, conseguimos definir as tensões:
E o que é que o exercício quer?
Basicamente, ele quer que a gente faça uma transformação de tensões.
Ele quer que a gente rotacione o elemento por um ângulo :
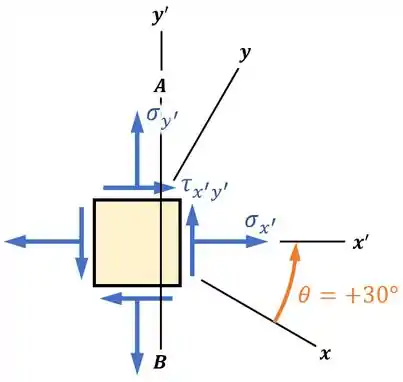
Ao fazemos isso, as novas tensões e que vão surgir vão corresponder (ser iguais) às tensões normal e cisalhante no plano , que é o que o exercício quer saber.
O exercício ainda quer que a gente resolve ele usando o Círculo de Mohr.
Então para resolver o exercício...
Devemos usar as tensões , & para desenhar um círculo de Mohr para esse elemento.
Feito isso, vamos rotacionar a reta do círculo de Mohr que diz as tensões no nosso eixo ( e ) por um ângulo , definindo assim as tensões num eixo ( e ).
Em seguida, vamos usar trigonometria (seno, cosseno, etc.) para decifrar os valores de e .
Por fim, esses valores vão corresponder às tensões e no plano pedidas pelo exercício, sendo assim as nossas respostas para o exercício.
Passo 2
Então vamos começar desenhando o nosso círculo de Mohr!
Lembra aí!
Já definimos as , & , então o próximo passo para desenhar o círculo de Mohr é calcular o valor de :
Agora, podemos desenhar os eixos e :
E marcar nele os pontos:
- ;
- & .
Marcados esses pontos, ligamos ele com uma reta e desenhamos o nosso círculo:
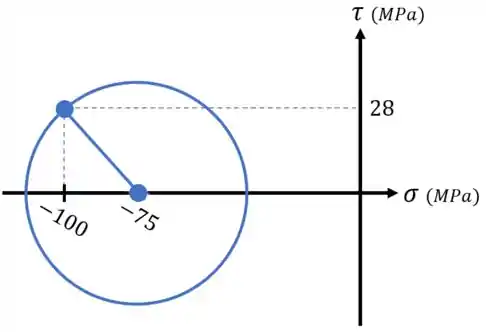
Passo 3
Agora, vamos rotacionar a reta do nosso círculo de Mohr usando um ângulo .
Aqui, devemos nos lembrar que:
- Enquanto que o ângulo no estado de tensões é positivo no sentido anti-horário;
- O ângulo no círculo de Mohr é positivo no sentido horário.
(Isso só não ocorre caso a gente opte por desenhar desde o começo o gráfico do Círculo de Mohr com o eixo apontando para baixo.)
Se lembrando disso, percebemos que essa rotação vai ser então uma rotação de no sentido horário:
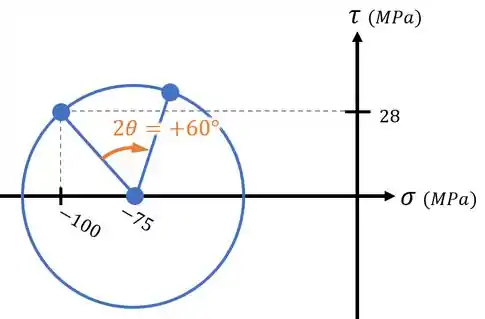
Aí, enquanto que a reta antiga definia as tensões antigas ( e ) no eixo , a reta nova vai definir as tensões novas ( e ) no eixo rotacionado :
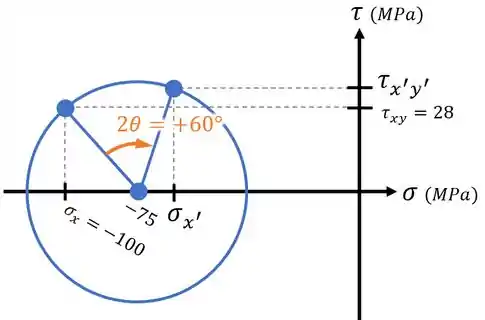
Passo 4
Definidas as tensões e no gráfico, precisamos agora usar trigonometria para encontra-las.
Para tanto, vamos focar no desenho abaixo, montado a partir dos dados do círculo de Mohr acima:
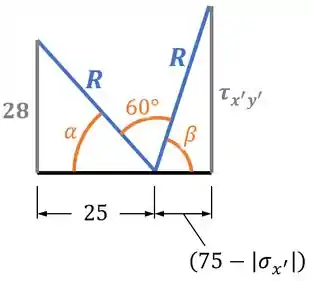
Primeiro, fazendo Pitágoras no triângulo esquerdo, temos:
O que significa que:
Além disso, podemos ver que a tangente do ângulo é:
Aí, colocando esse valor na função da nossa calculadora, encontramos que:
Em seguida, podemos perceber que:
Aí, isolando e substituindo , encontramos que:
Agora, podemos usar seno de para encontrarmos o valor de :
Isolando e substituindo e , encontramos que:
Calculando, isso dá:
Além disso, ainda podemos usar o cosseno de para encontrarmos o valor de :
Aí, isolando e substituindo e , encontramos:
O que dá:
Em seguida, isolando , encontramos que:
E por fim, como no gráfico é negativo, isso significa que:
E pronto!
Nosso exercício está resolvido, e, para fornecermos a nossa resposta, basta fazermos a correspondência das tensões encontradas para o eixo com as tensões no plano :
Resposta
Exercício Resolvido #4
Elaboração própria
Com base no elemento infinitesimal dado, determine:
- As tensões principais normais
- O cisalhante máximo
a partir do círculo de mohr.
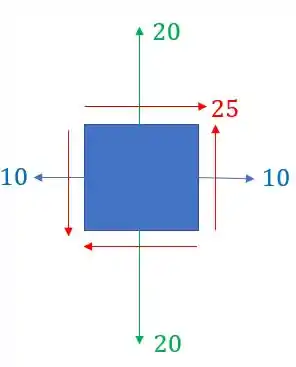
Passo 1
Como já vimos queremos determinar alguns valores com base no círculo de mohr, e para fazermos isso precismos desenhar o círculo de Mohr.
Sabemos que para fazer esse desenho necessitamos de dois pontos:
O primeiro é o ponto que marca o centro do círculo que é dado por
O segundo é o ponto que marca o fim do raio do círculo de mohr, que é dado por
Passo 2
Como já temos os valores para desenhar o círculo de mohr, vamos fazer os devidos desenhos e dessa forma começar a definir os valores pedidos no enunciado.
Sabemos que
Substituindo teremos que
Desenhando o círculo de mohr
Primeiro desenhamos o raio
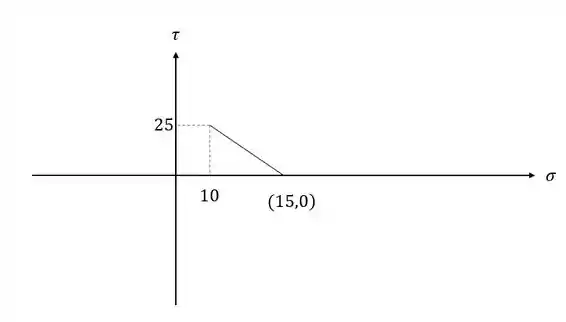
Depois desenhamos o círculo de mohr
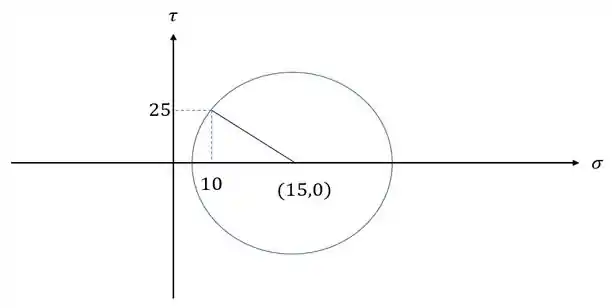
Passo 3
Agora que temos o círculo de mohr basta irmos definindo os valores pedidos no enunciado, então vamos lá.
Sabemos que as tensões principais Normais são dadas por
Em que só não temos o valor de R
Pode mos definir esse valor facilmente se observamos que o triangulo é retângulo
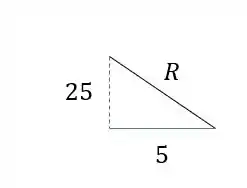
Usando pitagoras teremos que
Logo o valor de R será
Substituindo na nossa fórmula teremso que
Passo 4
No item B nos é pedido a tensão de cisalhemento máxima, que é o próprio valor de R, ou seja, do raio do círculo de mohr.
Logo o cisalhante máximo é
Resposta
a)
b)
Exercício Resolvido #5
Elaboração própria
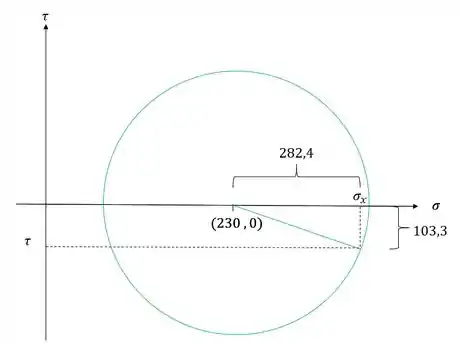
Abaixo é dado um círculo de mohr. Com base nele determine o valor das tensões , , e por fim desenhe o elemento infinitesimal relacioando a este círculo de mohr.
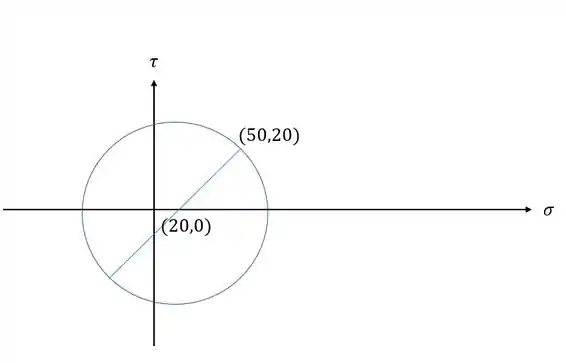
Passo 1
Antes de substituirmos qualquer valor vamos entender o que cada parte do nosso círculo de mohr representa.
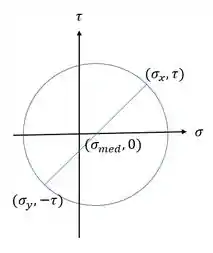
Sabemos que o valor central nós dá o valor de , o valor superior nos dará e o valor inferiro nos dará . Mas perceba que tanto o de cima quando o de baixo nós dará o valor de .
Passo 2
Agora que já definimos o que cada valor representa, basta tomar cuidado e definir facilmente cada um dos valores que nos é pedido.
Vamos analisar o triangulo que temos a partir do círculo de mohr.
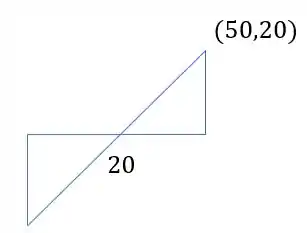
Definindo os valores de cada parte teremos, primeiro para parte superior do triangulo
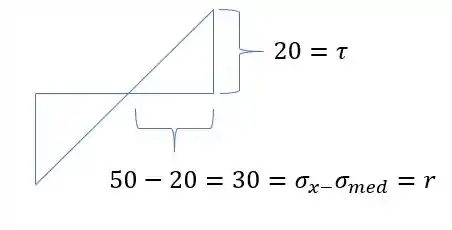
Em que podemos definir que
Analisando agora o triangulo abaixo teremos que
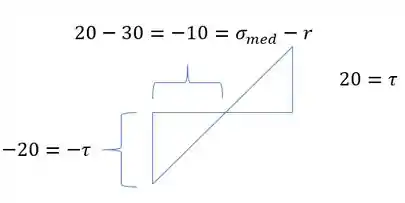
Em que podemos definir que
Ou seja, com o valor da tensão em y também confirmamos o valor do cisalhente.
Passo 3
Agora que já temos todos os valores, basta apenas desenhar o elemento, tomando cuidado com os sinais dos vetores.
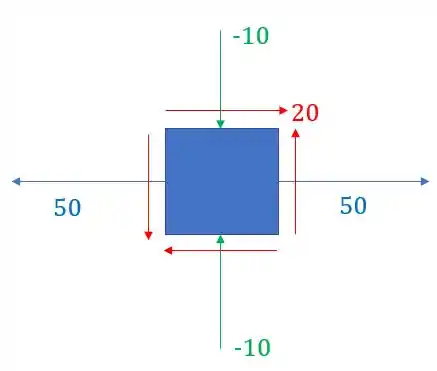
Resposta
Exercício Resolvido #6
Elaboração própria
Uma barra de ferro, responsável por manter duas articulações juntas, possui resistência adimissivel para tensões normais de 51Mpa e a tensões cisalhantes de 45 Mpa.
Sabendo disso e que nesta barra em um certo momento foi retirando um elemento infinitesimal dado abaixo, determine se esta barra rompera, ou não. Se romper, será devido a qual das tensões?
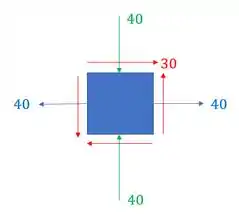
Passo 1
Como no exercício nos foi dado o valor das tensões admissíveis, precisamos determinar as tensões máximas que podem surgir nesse elemento, para isso dividiremos essa situação em duas partes.
Na primeira parte usaremos o círculo de Mohr para definirmos as tensões máximas existentes nesse elemnto.
Na segunda parte definiremos em que planos essas tensões máximas agem caso aja rompimento, se não houver rompimento não haverá necessidade de calcularmos os planos em que elas correm.
Passo 2
Como já vimos queremos determinar alguns valores com base no círculo de mohr, e para fazermos isso precismos desenhar o círculo de Mohr.
Sabemos que para fazer esse desenho necessitamos de dois pontos:
O primeiro é o ponto que marca o centro do círculo que é dado por
O segundo é o ponto que marca o fim do raio do círculo de mohr, que é dado por
Como já temos os valores para desenhar o círculo de mohr, vamos fazer os devidos desenhos e dessa forma começar a definir os valores pedidos no enunciado.
Sabemos que
Substituindo teremos que
Passo 3
Desenhando o círculo de mohr teremos que
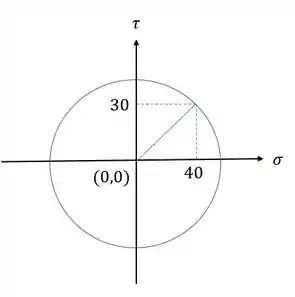
Como já temos o valor de basta apenas determinarmos o valor de R usando o triangulo retângulo da figura.
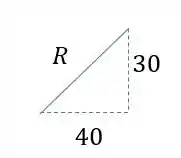
Fazendo essa conta teremos que
Logo
Passo 4
Agora precisamos ver todas as tensões máximas.
Primeiro vamos ver as normais
Como a resistência admissível para tensões normais é de 52Mpa, nosso material não romperá por tensões normais já que o máximo alcançado é de 50 Mpa.
Com relação a tensão cisalhante sabemos que o máximo alcançado é de exatamente o valor do raio do nosso círculo, logo o valor de .
Como a resistência do nosso material a tensões cisalhantes é de 45Mpa, ele romperá devido a tensão cislhante máxima. Mas em que plano?
Passo 5
Sabemos que a fórmula que nos dá o plano em que ocorrem as tensões principais é dado por
Substituindo os valores teremos que
O que é importante ressaltar aqui é que esses ângulos representam os planos em que ocorrem as tensões principais, e não a cisalhante, para descobrir a cisalhante é necessário somar e subtrair 45°
Logo os ângulos serão:
Ou
Resposta
O rompimento ocorre devido a tensão cisalhamte máxima de 50MPa e que ocorre nos planos de 63,5° ou -26,5°.
Exercício Resolvido #7
Elaboração própria
Dado o elemento infinitesimal abaixo, determine o valor mínimo da tensão cisalhante em função da tensão no eixo x para que não ocorra rompimento do material que possui tensão admissível de 50Mpa para tensões normais.
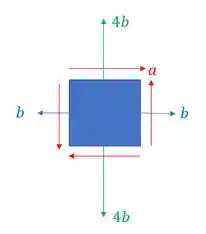
Passo 1
Como já vimos queremos determinar alguns valores com base no círculo de mohr, e para fazermos isso precismos desenhar o círculo de Mohr.
Sabemos que para fazer esse desenho necessitamos de dois pontos:
O primeiro é o ponto que marca o centro do círculo que é dado por
O segundo é o ponto que marca o fim do raio do círculo de mohr, que é dado por
Passo 2
Como já temos os valores para desenhar o círculo de mohr, vamos fazer os devidos desenhos e dessa forma começar a definir os valores pedidos no enunciado.
Sabemos que
Substituindo teremos que
Passo 3
Desenhando o círculo de Mohr teremos que
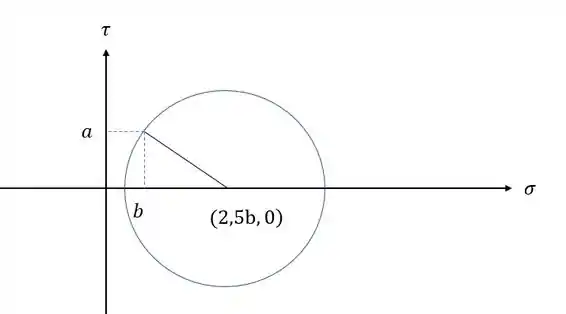
Olhando o nosso triangulo teremos que
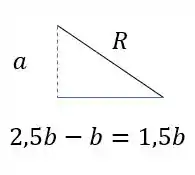
Fazendo pitagora teresmo que
As nossas tensões principais são dadas por
Em que
E nesse caso como queremos saber o limite do rompimento, usaremos
Substituindo tudo teremos que
Isolando a raiz, teremos que
Elevando os valores de ambos os lados ao quadrado teremos que
Isolando cada letra de um lado teremos que
Podemos simplificar essa solução escrevendo a solução como
Resposta
Exercício Resolvido #8
Elaboração própria
O elemento infinitesimal abaixo foi rotacionado de 30° no sentido horário. Usando o círculo de Mohr, determine quais serão as tensões nesse plano a 30°.
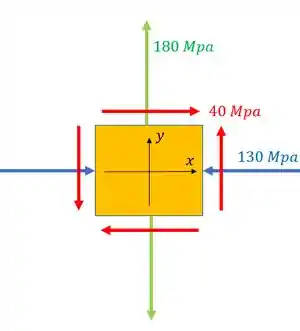
Passo 1
Como já vimos queremos determinar alguns valores com base no círculo de mohr, e para fazermos isso precisamos desenhar o círculo de Mohr.
Sabemos que para fazer esse desenho necessitamos de dois pontos:
O primeiro é o ponto que marca o centro do círculo que é dado por
O segundo é o ponto que marca o fim do raio do círculo de mohr, que é dado por
Passo 2
Como já temos os valores para desenhar o círculo de mohr, vamos fazer os devidos desenhos e dessa forma começar a definir os valores pedidos no enunciado.
Sabemos que
Substituindo teremos que
Desenhando o círculo de mohr
Primeiro desenhamos o raio
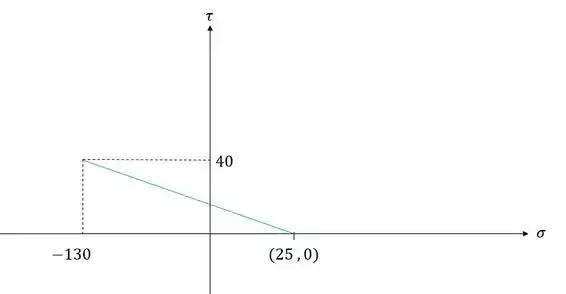
Depois desenhamos o círculo de mohr
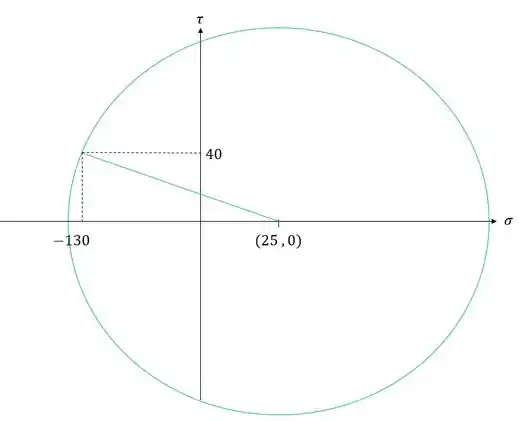
Passo 3
Agora que já temos o círculo de mohr precisamos lembrar como ele funciona quando fazemos a rotação do nosso elemento infinitesimal.
O primeiro conceito que temos que lembrar é que todo sentido que rotacionamos o nosso elemento é o contrario no círculo de mohr, por exemplo, se rotacionamos nosso elemento no sentido horário, no círculo de mohr faremos esse giro no sentido anti-horário.
Outra coisa que precisamos saber é que no círculo de mohr o número de graus que andaremos será o dobro do numero de graus que andamos no elemento, ou seja, no nosso caso andamos 30°, logo no círculo de mohr teremos que andar 60°.
Juntando os dois conceitos teremos que rotacionar, a partir do raio que desenhamos o círculo de mohr, 60° no sentido anti-horário. Na imagem abaixo podemos ver bem como devemos fazer isso.
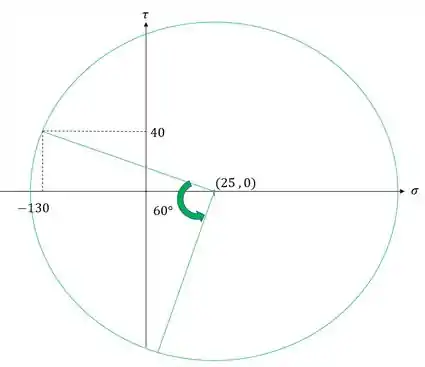
Outra coisa que precisamos notar são os dois triângulos da nossa figura, um triangulo para os valores iniciais e outro para os valores finais, que podemos ver abaixo
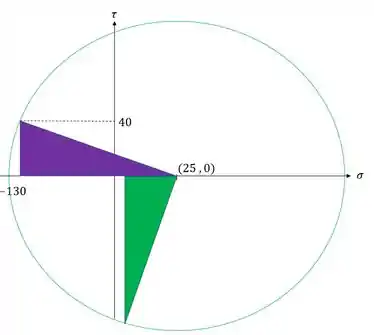
Sabemos que podemos determinar algumas coisas relacionadas aos triângulos,
Começando pelo triangulo roxo sabemos que podemos determinar o valor dos catetos, como vemos na figura
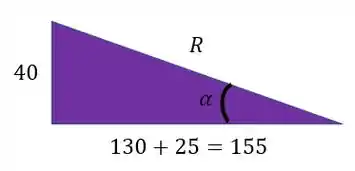
Se temos os valores dos catetos, podemos determinar facilmente o valor da hipotenusa pelo teorema de Pitágoras, lembrando que a hipotenusa do nosso triangulo simboliza exatamente o raio do nosso círculo de mohr.
Como já temos os valores dos catetos e da hipotenusa podemos também determinar o valor de , com isso teremos que
Mas porque calculamos esse ângulo? Veremos no próximo passo que ele nos ajudará nos cálculos do próximo triangulo, então vamos lá.
Passo 4
Como já analisamos o que tínhamos no triangulo roxo, vamos ver agora o que conseguimos determinar no triangulo verde.
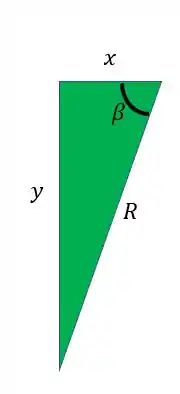
Dessas incógnitas sabemos que a hipotenusa desse triangulo também é o raio do nosso círculo, que já determinamos no passo anterior
Para determinarmos o valor de basta olharmos o seguinte
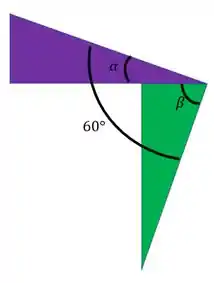
Com isso podemos ver que
Como já temos o valor de fica fácil determinarmos o valor de
Olhando o nosso triangulo teremos que usar relações trigonométricas para encontrarmos os valores desejados
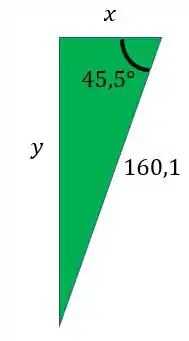
Sabemos que
Agora que já temos os valores vamos determinar o que eles representam no nosso círculo de mohr
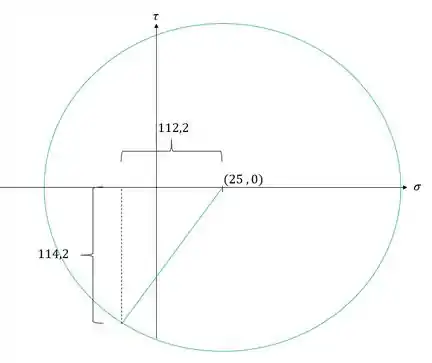
Pelo círculo de mohr teremos que
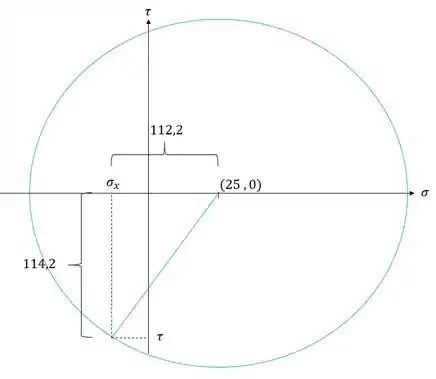
Para determinarmos a tensão normal em y basta analisarmos o prolongamento do raio
Resposta
Exercício Resolvido #9
Elaboração própria
O elemento infinitesimal abaixo foi rotacionado de 57° no sentido anti-horário. Usando o círculo de Mohr, determine quais serão as tensões nesse plano a 57°.
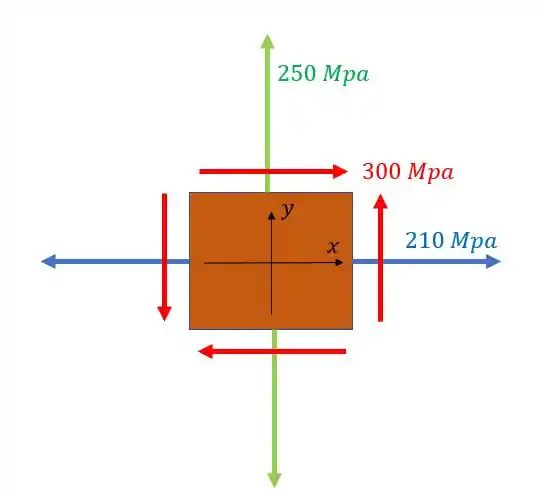
Passo 1
Como já vimos queremos determinar alguns valores com base no círculo de mohr, e para fazermos isso precisamos desenhar o círculo de Mohr.
Sabemos que para fazer esse desenho necessitamos de dois pontos:
O primeiro é o ponto que marca o centro do círculo que é dado por
O segundo é o ponto que marca o fim do raio do círculo de mohr, que é dado por
Passo 2
Como já temos os valores para desenhar o círculo de mohr, vamos fazer os devidos desenhos e dessa forma começar a definir os valores pedidos no enunciado.
Sabemos que
Substituindo teremos que
Desenhando o círculo de mohr
Primeiro desenhamos o raio
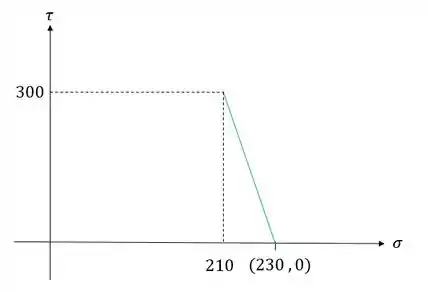
Depois desenhamos o círculo de mohr
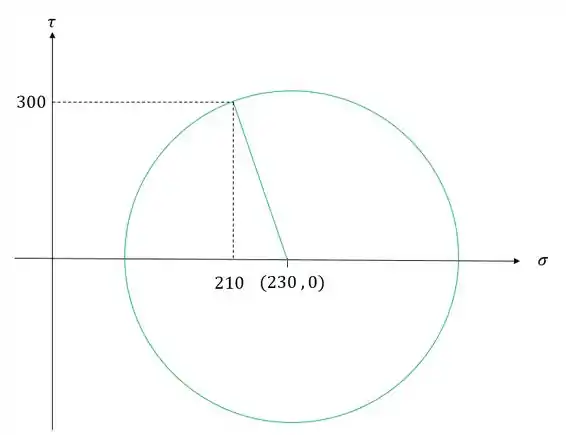
Passo 3
Agora que já temos o círculo de mohr precisamos lembrar como ele funciona quando fazemos a rotação do nosso elemento infinitesimal.
O primeiro conceito que temos que lembrar é que todo sentido que rotacionamos o nosso elemento é o contrario no círculo de mohr, por exemplo, se rotacionamos nosso elemento no sentido horário, no círculo de mohr faremos esse giro no sentido anti-horário e vice versa.
Outra coisa que precisamos saber é que no círculo de mohr o número de graus que andaremos será o dobro do número de graus que andamos no elemento, ou seja, no nosso caso andamos 57°, logo no círculo de mohr teremos que andar 114°.
Juntando os dois conceitos teremos que rotacionar, a partir do raio que desenhamos o círculo de mohr, 114° no sentido horário. Na imagem abaixo podemos ver bem como devemos fazer isso.
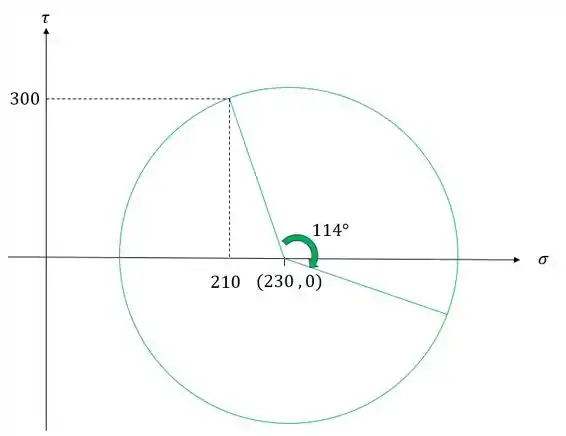
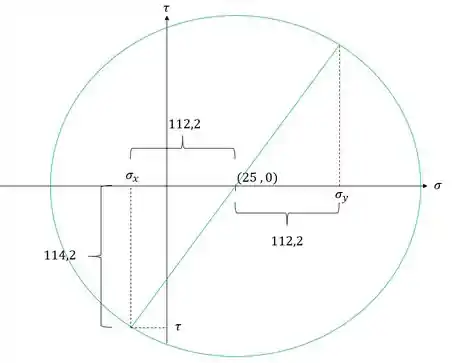
Outra coisa que precisamos notar são os dois triângulos da nossa figura, um triangulo para os valores iniciais e outro para os valores finais, que podemos ver abaixo
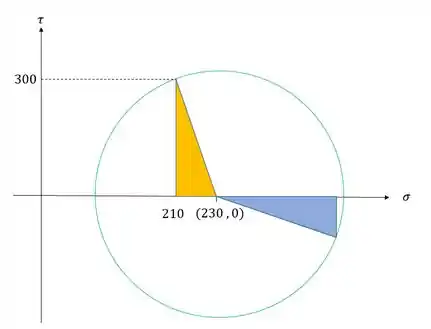
Sabemos que podemos determinar algumas coisas relacionadas aos triângulos,
Começando pelo triangulo amarelo sabemos que podemos determinar o valor dos catetos, como vemos na figura
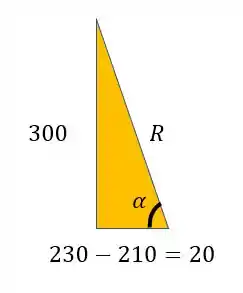
Se temos os valores dos catetos, podemos determinar facilmente o valor da hipotenusa pelo teorema de Pitágoras, lembrando que a hipotenusa do nosso triangulo simboliza exatamente o raio do nosso círculo de mohr.
Como já temos os valores dos catetos e da hipotenusa podemos também determinar o valor de , com isso teremos que
Mas porque calculamos esse ângulo? Veremos no próximo passo que ele nos ajudará nos cálculos do próximo triangulo, então vamos lá.
Passo 4
Como já analisamos o que tínhamos no triangulo amarelo, vamos ver agora o que conseguimos determinar no triangulo azul.
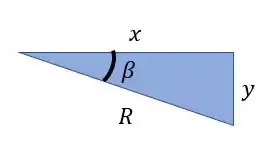
Dessas incógnitas sabemos que a hipotenusa desse triangulo também é o raio do nosso círculo, que já determinamos no passo anterior
Para determinarmos o valor de basta olharmos o seguinte
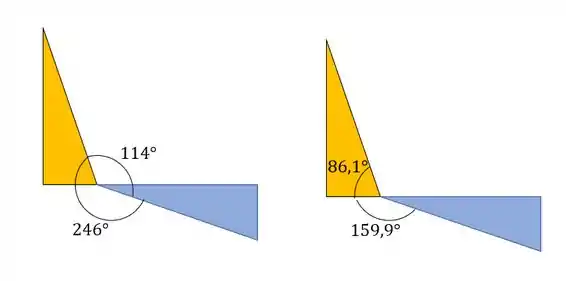
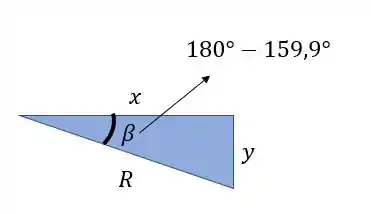
Com isso podemos ver que
Olhando o nosso triangulo teremos que usar relações trigonométricas para encontrarmos os valores desejados
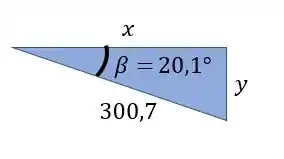
Sabemos que
Agora que já temos os valores vamos determinar o que eles representam no nosso círculo de mohr
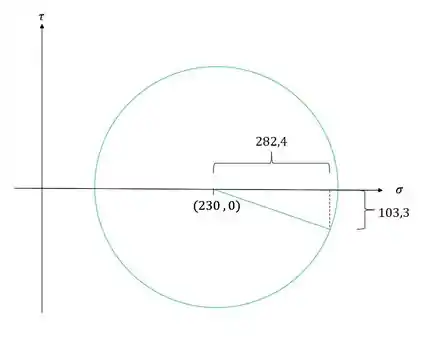
Pelo círculo de mohr teremos que
Para determinarmos a tensão normal em y basta analisarmos o prolongamento do raio
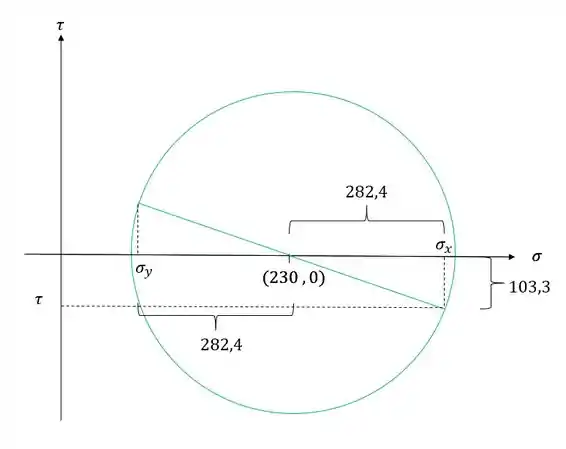
Como deu negativo significa que nosso círculo de mohr deveria ser mais para a esquerda como mostra figura