Teoria
Introdução
Como é muito importante sempre definirmos a nossas estruturas, precisamos saber o que é uma grelha.
Uma grelha é uma estrutura tridimensional que possui a ação apenas e somente de momentos fletores e cargas verticais, não possuindo de forma alguma, ações horizontais.
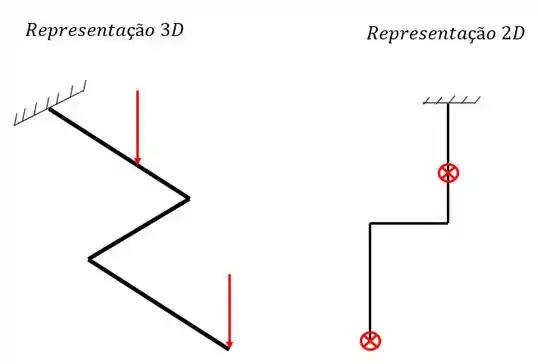
Aqui vemos um novo conceito, agora não olhamos mais a nossa barra de perfil, como fazíamos nas treliças, pórticos e vigas, agora olhamos a nossa barra de cima, e por isso representamos o vetor entrando na tela como um x. vamos então entender algumas representações novas que a grelha irá trazer na sua representação.
Representação dos vetores
No caso das grelhas, teremos apenas vetores verticais e momentos fletores, no caso a representação será feita por
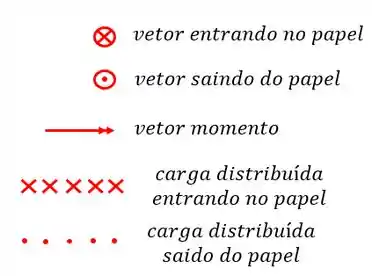
Lembrando que as reações de apoio também serão verticais, não havendo, nesse caso, representação horizontal para forças horizontais, já que nas nossas grelhas as consideramos inexistentes.
Representação dos apoios
Os apoios também vão ter representações especificas, vamos entender como representar esses apoios quando olhados de cima. Vale lembrar que como não temos cargas verticais então usaremos apoios de primeiro gênero, isso para deixar claro que a nossa estrutura não absorve nenhuma força horizontal.
- Apoio do primeiro gênero
- Apoios de momentos
- Rótula
- Charneira ou dobradiça
- Tri apoiadas
- Rotuladas
- Com charneira
- Compostas
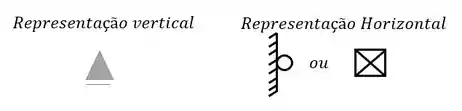
Veja que a representação é diferente do que estamos acostumados, ou seja, se a nossa grelha fosse assim
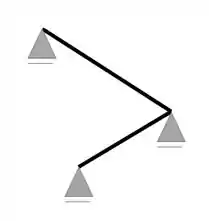
A representaríamos assim
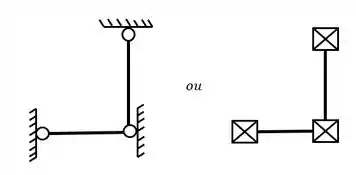
Os apoios de momentos nós já conhecemos um que é o engaste, que no primeiro exemplo da nossa aula nós já vimos que a representação vertical e horizontal é idêntica. Mas tem um novo tipo de apoio, que nós chamamos de Charneira.
A charneira é tipo uma dobradiça de porta, ela permite que a nossa porta gire em torno da dobradiça, mas impede que a porta se movimente na vertical e na horizontal.

O que vale destacar é, como a dobradiça permite rotação, podemos dizer que o somatório de momentos fletor nela é igual a zero, porém a dobradiça impede momentos de torção, então sabemos que um dos esforços que pode aparecer nela é a torção. Isso vai ajudar a gente nos cálculos de esforços.
Representação das rótulas
Para as rótulas nós teremos dois tipos
Essa já é nossa antiga conhecida, sabemos que ela não transfere nenhum momento para outra barra e a sua representação é a mesma
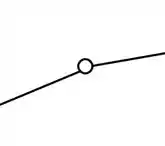
O que temos que tomar cuidado é que quando cortarmos ela, no caso de grelhas compostas, teremos um apoio do primeiro gênero, e sua representação será
Essa conhecemos nessa aula, vimos que ela permite rotação, mas impede torção e movimento entre barras, e no caso de rótula a sua representação será
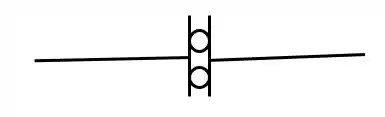
Da mesma forma, o que temos que tomar cuidado é que, em grelhas compostas, quando quebrarmos ela, teremos que ela virará uma dobradiça de apoio, e sua representação passa a ser

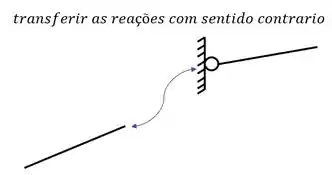
Outro ponto importante é que as charneiras dependem do ângulo que fazem com a barra, pois o momento torsor que elas impedem são sempre perpendiculares a sua direção, por exemplo
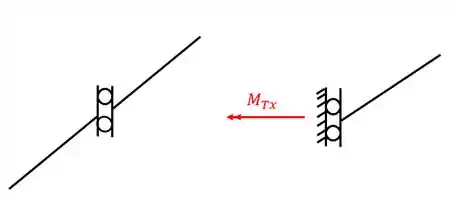
Nesse caso em que a charneira é vertical, a reação ao momento torsor terá apenas uma componente horizontal, porém e se a charneira estiver inclinada?
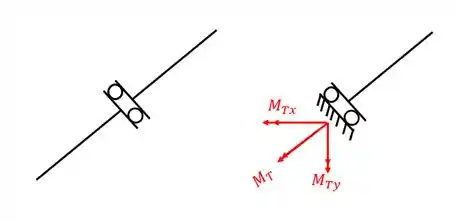
Nesse caso vemos que a reação ao momento torsor ainda é perpendicular a charneira, porém, para fins de cálculo teríamos que decompor o valor desse momento para podermos fazer o equilíbrio.
Com isso terminamos todas as possíveis representações que poderiam aparecer para as grelhas que iremos resolver na aula de solução de grelhas simples e na aula de grelhas compostas.
Tipos de grelhas
Vale destacar que para grelhas usaremos o mesmo método de determinação de estrutura isostática. Devemos ver se a grelha fica em equilíbrio com os apoios que possui, lembrando que ignoramos efeitos horizontais. O número de incógnitas sempre é dado pelos apoios e as rótulas sempre dão equações.
Apoios do primeiro gênero darão apenas 1 incógnita. Engastes darão 3 incógnitas, sendo uma vertical, um momento fletor e um momento torsor. Charneiras darão 2 incógnitas, uma vertical e um momento torsor. Rótulas quebradas darão apenas uma incógnita, que será sempre reação vertical. Com relação as equações já conhecemos as 3 de equilíbrio, que no caso substituiremos a de forças horizontais por somatório de torsores igual a zero. E com relação as rótulas explicaremos melhor nos tipos de grelhas dadas abaixo.
as grelhas tri apoiadas são aquelas que necessitam de 3 apoios para ficarem em equilíbrio, na nossa aula já vimos uma grelha dessas
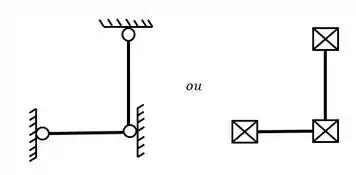
São grelhas que possuem uma rótula, lembrando que a rótula sempre nos ajuda na contagem de equações. Uma rótula que possui duas barras chegando nela, nos dará mais 1 equação, se tiver 3 barras, 2 equações, sempre o número de equações que a rótula nos dá é igual ao número de barras que chegam nessa rótula subtraído de 1
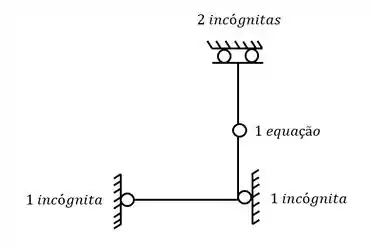
Por exemplo, nesse caso temos 4 incógnitas, e se não houvesse a rótula, teríamos apenas 3 equações. Com a presença da rótula passamos a ter uma estrutura isostática. Se não houvesse a rótula teríamos uma estrutura hiperestática, já que teríamos mais incógnitas que equações. E se colocássemos ao invés de 1 mas 2 rótulas, teríamos uma estrutura hipostática, já que teríamos mais equações que incógnitas.
Como vimos, a charneira impede momento torsor, e também movimentação vertical, então temos que saber que sempre que houver charneira devemos nos atentar para qual será o momento torsor e efeitos verticais que agiram sobre ela, ou seja, sempre duas incógnitas, como na imagem ali em cima.
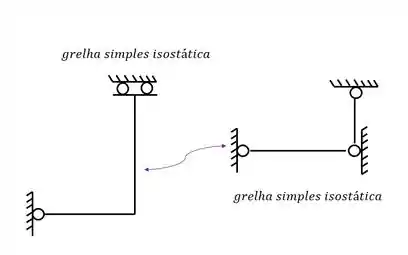
Grelhas compostas são grelhas compostas de grelhas simples, que separaremos sempre quebrando na rótula ou na charneira e colocaremos apoios fictícios, e transferiremos as reações dos apoios fictícios para as grelhas ao quais esses apoios estiverem apoiados.
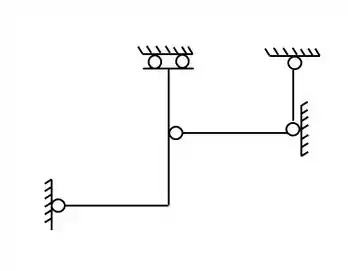
Quebrando na rótula teremos que
Agora que já entendemos os conceitos, vamos fazer os exercícios, e a partir disso podemos ir para aula de solução de grelhas. Vamos lá?

Representação dos vetores
Representação dos apoios
Representação das rótulas
Tipos de grelhas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
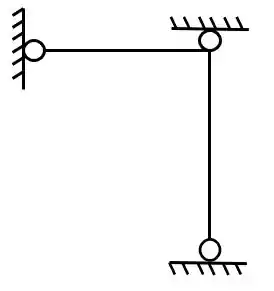
Represente a grelha 2D abaixo em uma grelha 3D.
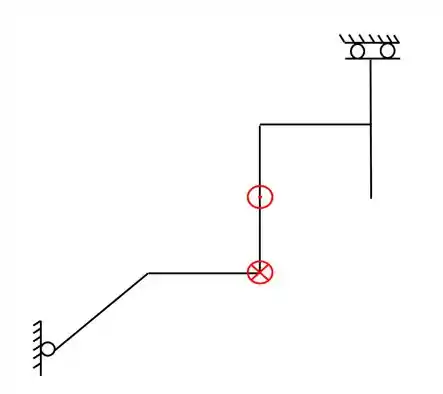
Passo 1
Sabemos que para representar as nossas grelhas em 3D precisamos identificar o que cada parte dela significa, para isso devemos seguir o seguinte passo a passo.
- Primeiro devemos identificar o que os apoios representam
- Depois devemos identificar o que as cargas representam
- Em seguida devemos lembrar que a representação 2D é como se víssemos a nossa grelha de cima
- Por fim juntamos todos os dados anteriores e montamos a nossa grelha
Vamos aplicar esse passo a passo no nosso exercício?
Passo 2
Sabemos que a primeira coisa que devemos fazer é identificar o que os nossos apoios representam, dessa forma, olhando a nossa grelha devemos observar quais são os seus apoios
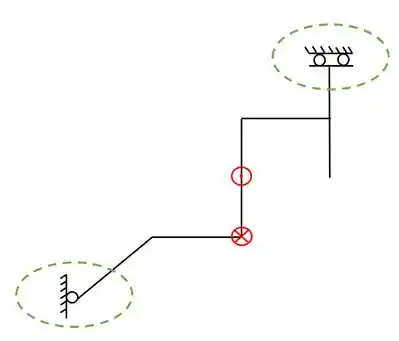
E devemos nos lembrar o que eles representavam na teoria, dessa forma saberemos que
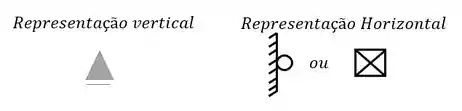
Com isso já sabemos que o nosso apoio da parte de baixo é um apoio do primeiro gênero, para o outro apoio devemos nos lembrar que
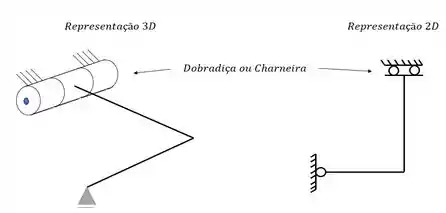
Ou seja, o nosso outro apoio representa um apoio do tipo Dobradiça ou charneira. Resolvido os apoios, vamos aos carregamentos.
Passo 3
Agora precisamos identificar os carregamentos, dessa forma devemos nos lembrar do que vimos novamente na teoria, com isso teremos que

Olhando nossa grelha teremos
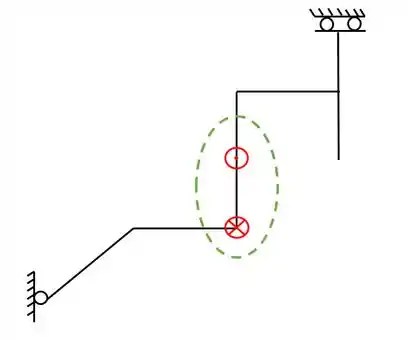
Ou seja, um carregamento entrando e um saindo da nossa folha, agora só falta representarmos as nossas barras em 3 dimensões.
Passo 4
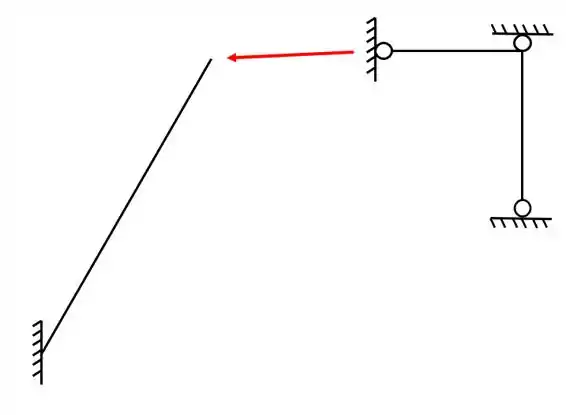
Lembrando que olhamos a nossa grelha de cima, vamos representa-la como se olhássemos ela em perspectiva, com isso, olhando só as barras, teríamos a seguinte forma
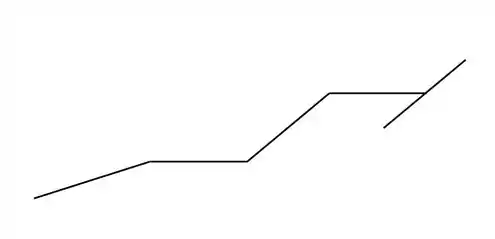
Colocando os apoios teremos que
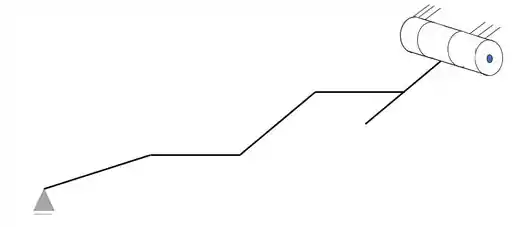
E colocando os carregamentos teremos que
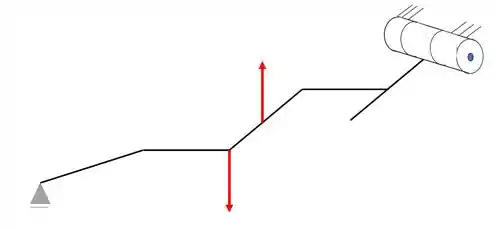
Logo, essa é a representação da nossa grelha em 3D
Resposta
Representação da grelha em 3D
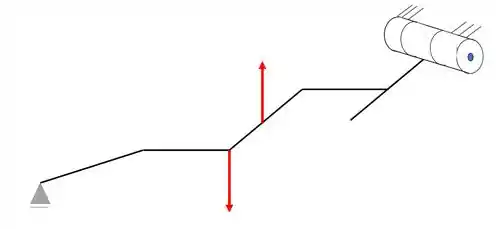
Exercício Resolvido #2
Elaboração Própria
Represente a grelha 3D abaixo em uma grelha 2D
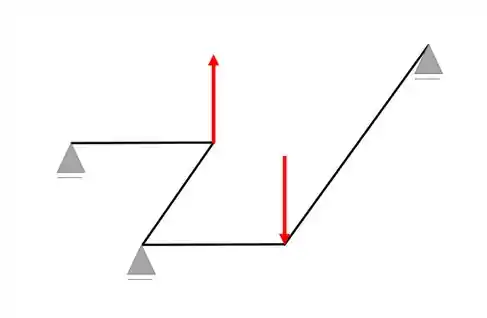
Passo 1
Sabemos que para representar as nossas grelhas em 2D precisamos identificar o que cada parte dela significa, para isso devemos seguir o seguinte passo a passo.
- Primeiro devemos identificar o que os apoios representam
- Depois devemos identificar o que as cargas representam
- Em seguida devemos lembrar que a representação 2D é como se víssemos a nossa grelha de cima
- Por fim juntamos todos os dados anteriores e montamos a nossa grelha
Vamos aplicar esse passo a passo no nosso exercício?
Passo 2
Sabemos que a primeira coisa que devemos fazer é identificar o que os nossos apoios representam, dessa forma, olhando a nossa grelha devemos observar quais são os seus apoios
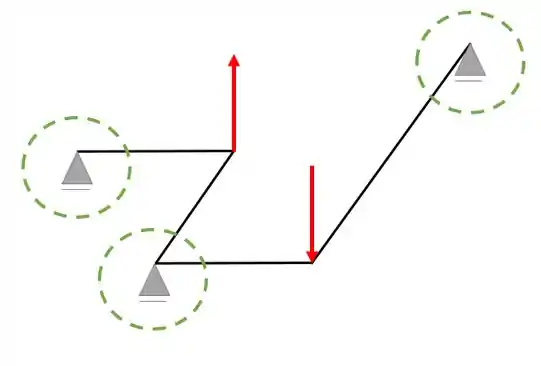
E devemos nos lembrar o que eles representavam na teoria, dessa forma saberemos que
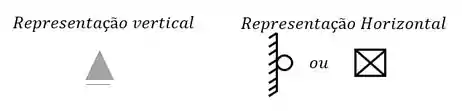
Com isso já sabemos que os nossos apoios são apoios do primeiro gênero.
Passo 3
Agora precisamos identificar os carregamentos, dessa forma devemos nos lembrar do que vimos novamente na teoria, com isso teremos que

Olhando nossa grelha teremos
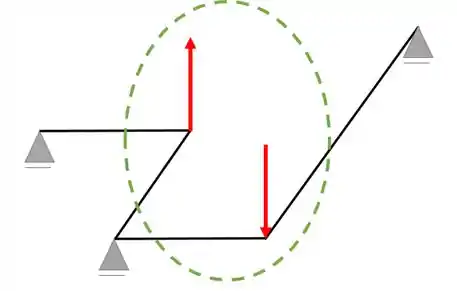
Ou seja, um carregamento entrando e um saindo da nossa folha, agora só falta representarmos as nossas barras em 2 dimensões.
Passo 4
Lembrando que olhamos a nossa grelha em perspectiva, vamos representa-la como se olhássemos ela de cima, com isso, olhando só as barras, teríamos a seguinte forma
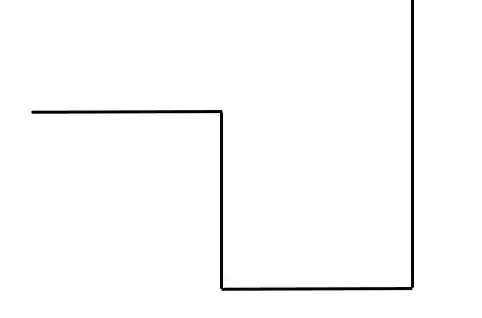
Colocando os apoios teremos que
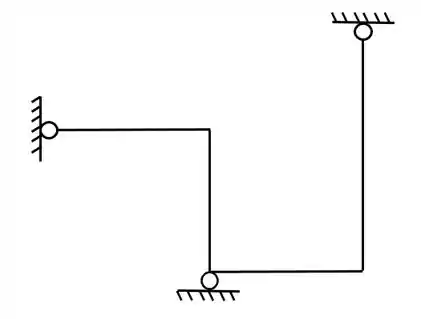
E colocando os carregamentos teremos que
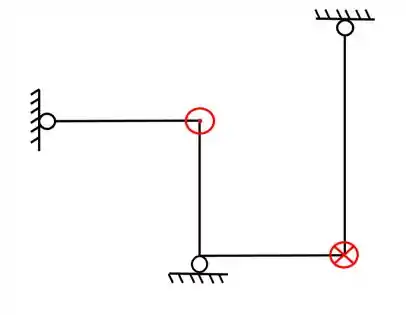
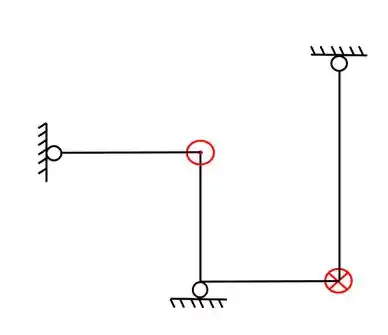
Logo, essa é a representação da nossa grelha em 2D
Resposta
Representação da grelha em 2D
Exercício Resolvido #3
Elaboração Própria
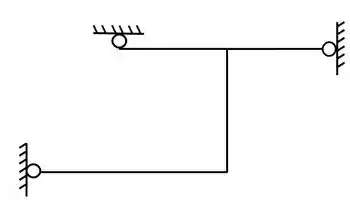
Faça a separação da grelha abaixo em grelhas simples (Lembrar de sempre quebrar nas rótulas)
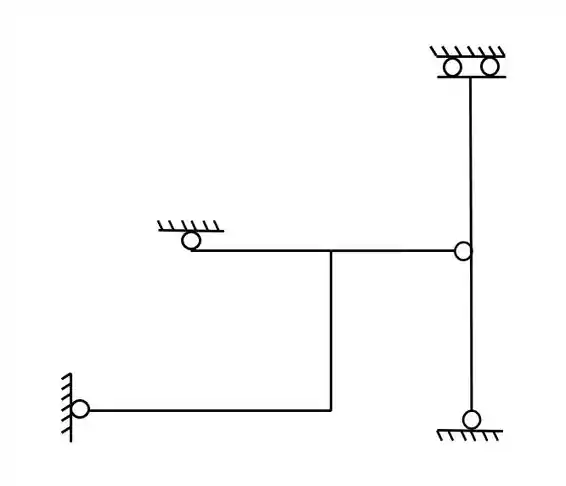
Passo 1
Sabemos que para separarmos a nossa grelha, sempre fazemos o rompimento em um nó com rótula, e depois verificamos se o número de equações (3 de equilíbrio) é compatível com o número de incógnitas (vindas do apoio e que sendo 3 equações de equilíbrio, precisaremos de 3 incógnitas por estrutura). Se o número de equações e de incógnitas for igual, sabemos que teremos feito a separação corretamente, então nosso passo a passo é simples.
- Primeiro achamos as possíveis rótulas a serem rompidas
- Em segundo trocamos a rótula rompida por um apoio fictício
- Por fim verificamos se cada estrutura tem 3 equações de equilíbrio e 3 incógnitas, se bater é porque dividimos certinho.
Vamos aplicar isso ao nosso exercício?
Passo 2
Como vimos primeiro devemos achar as possíveis rótulas a serem rompidas, e no nosso exemplo só temos uma possível rótula a ser rompida, que marcamos aqui em baixo.
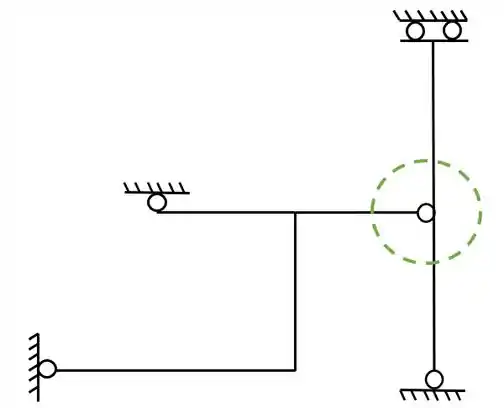
se lembrarmos o que vimos na aula teórica, lembraremos que o rompimento de rótulas gera apoios do primeiro gênero, e o rompimento de dobradiças, geram também, dobradiças.
Porém, vamos ao próximo passo então.
Passo 3
O segundo passo consiste em olharmos a nossa estrutura separada e com o apoio fictício
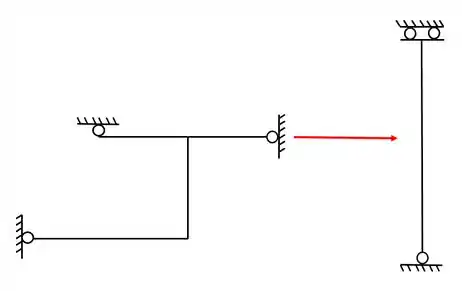
E como podemos ver, de fato se trata de um apoio do primeiro gênero.
Passo 4
Por fim precisamos fazer o balanceamento de equações e incógnitas das nossas estruturas, já sabemos que temos 3 equações de equilíbrio, que serão mais especificadas nas próximas aulas. E quanto aos apoios sabemos que dobradiças geram 2 incógnitas
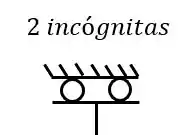
E que apoios do primeiro gênero apenas 1 incógnita

Dessa forma olhando cada estrutura separadamente, teremos que
- Primeira estrutura
- Segunda estrutura
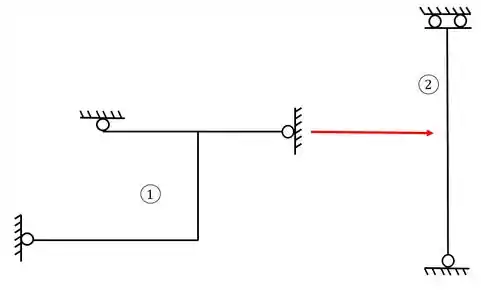
Vemos que ela possui 3 apoios do primeiro gênero, logo, possui 3 incógnitas, já que cada apoio gera uma incógnita. Como temos 3 incógnitas e 3 equações, sabemos que a nossa estrutura foi dividida corretamente.

Vemos que ela possui 1 dobradiça e 1 apoio do primeiro gênero, logo, possui 3 incógnitas, já que o apoio gera uma incógnita e a dobradiça gera 2. Como temos 3 incógnitas e 3 equações, sabemos que a nossa estrutura foi dividida corretamente.
E dessa forma ao invés de resolvermos uma estrutura muito complexa de grelhas, resolveríamos duas mais simples.
Resposta
A separação da grelha será
Exercício Resolvido #4
Elaboração Própria
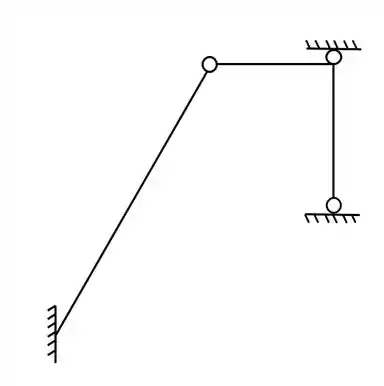
Faça a separação da grelha abaixo em grelhas simples (Lembrar de sempre quebrar nas rótulas)
Passo 1
Sabemos que para separarmos a nossa grelha, sempre fazemos o rompimento em um nó com rótula, e depois verificamos se o número de equações (3 de equilíbrio) é compatível com o número de incógnitas (vindas do apoio e que sendo 3 equações de equilíbrio, precisaremos de 3 incógnitas por estrutura). Se o número de equações e de incógnitas for igual, sabemos que teremos feito a separação corretamente, então nosso passo a passo é simples.
- Primeiro achamos as possíveis rótulas a serem rompidas
- Em segundo trocamos a rótula rompida por um apoio fictício
- Por fim verificamos se cada estrutura tem 3 equações de equilíbrio e 3 incógnitas, se bater é porque dividimos certinho.
Vamos aplicar isso ao nosso exercício?
Passo 2
Como vimos primeiro devemos achar as possíveis rótulas a serem rompidas, e no nosso exemplo só temos uma possível rótula a ser rompida, que marcamos aqui em baixo.
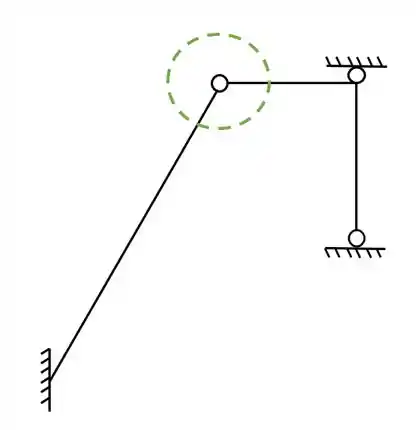
se lembrarmos o que vimos na aula teórica, lembraremos que o rompimento de rótulas gera apoios do primeiro gênero, e o rompimento de dobradiças, geram também, dobradiças.
Porém, vamos ao próximo passo então.
Passo 3
O segundo passo consiste em olharmos a nossa estrutura separada e com o apoio fictício
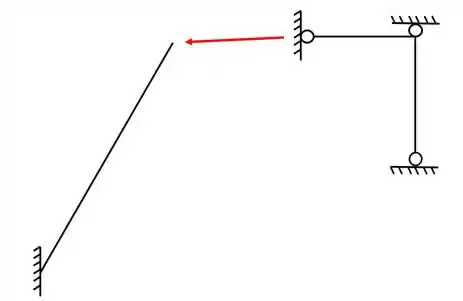
E como podemos ver, de fato se trata de um apoio do primeiro gênero.
Passo 4
Por fim precisamos fazer o balanceamento de equações e incógnitas das nossas estruturas, já sabemos que temos 3 equações de equilíbrio, que serão mais especificadas nas próximas aulas. E quanto aos apoios sabemos que dobradiças geram 2 incógnitas
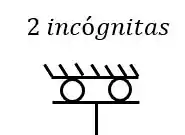
que apoios do primeiro gênero apenas 1 incógnita

E que os engastes geram 3 incógnitas
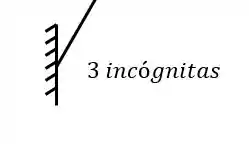
Dessa forma olhando cada estrutura separadamente, teremos que
- Primeira estrutura
- Segunda estrutura
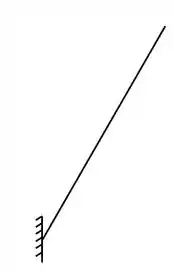
Vemos que ela possui 1 apoio de engaste, ou, do terceiro gênero, logo, possui 3 incógnitas. Como temos 3 incógnitas e 3 equações, sabemos que a nossa estrutura foi dividida corretamente.
Vemos que ela possui 3 apoios do primeiro gênero, logo, possui 3 incógnitas, já que cada apoio gera uma incógnita. Como temos 3 incógnitas e 3 equações, sabemos que a nossa estrutura foi dividida corretamente.
E dessa forma ao invés de resolvermos uma estrutura muito complexa de grelhas, resolveríamos duas mais simples.
Resposta
A separação da grelha será
Exercício Resolvido #5
Elaboração Própria
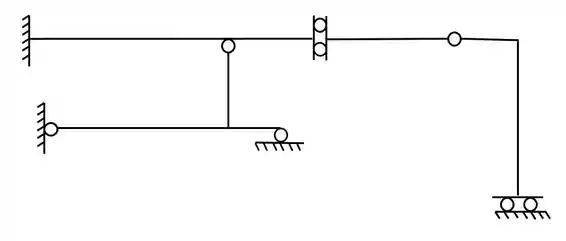
Faça a separação da grelha abaixo em grelhas simples (Lembrar de sempre quebrar nas rótulas)
Passo 1
Sabemos que para separarmos a nossa grelha, sempre fazemos o rompimento em um nó com rótula, e depois verificamos se o número de equações (3 de equilíbrio) é compatível com o número de incógnitas (vindas do apoio e que sendo 3 equações de equilíbrio, precisaremos de 3 incógnitas por estrutura). Se o número de equações e de incógnitas for igual, sabemos que teremos feito a separação corretamente, então nosso passo a passo é simples.
- Primeiro achamos as possíveis rótulas a serem rompidas
- Em segundo trocamos a rótula rompida por um apoio fictício
- Por fim verificamos se cada estrutura tem 3 equações de equilíbrio e 3 incógnitas, se bater é porque dividimos certinho.
Vamos aplicar isso ao nosso exercício?
Passo 2
Como vimos primeiro devemos achar as possíveis rótulas a serem rompidas, e no nosso exemplo só temos uma possível rótula a ser rompida, que marcamos aqui em baixo.
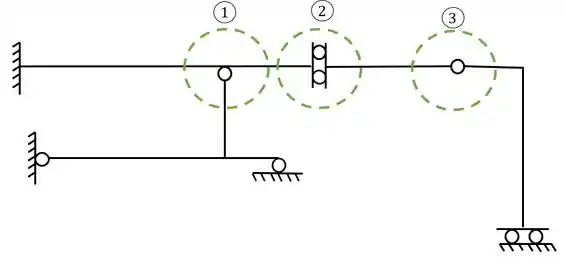
se lembrarmos o que vimos na aula teórica, lembraremos que o rompimento de rótulas gera apoios do primeiro gênero, e o rompimento de dobradiças, geram também, dobradiças.
Porém, vamos ao próximo passo então.
Passo 3
O segundo passo consiste em olharmos a nossa estrutura separada e com o apoio fictício, mas onde podemos romper? Perceba que a rótula 1 é uma ótima rótula a ser rompida, rompendo ela, teríamos
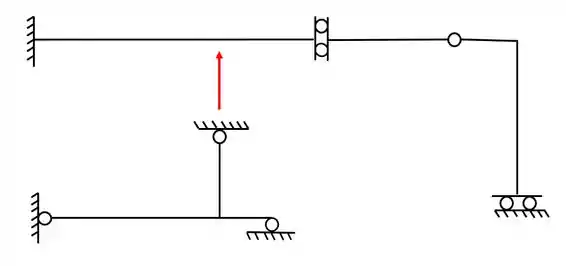
Agora pode surgir a duvida se rompemos a rótula 2 ou 3. Nesse caso basta ver o seguinte. O apoio mais a esquerda é um engaste, logo sabemos que ele pode ficar sozinho. Se rompermos a rótula 3, a nossa dobradiça ficará junta com o engaste, o que não nos ajuda, mas se rompermos a dobradiça, teremos o engaste sozinho, o que nos ajuda, dessa forma, a solução ficará
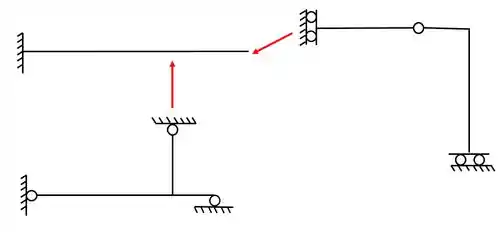
Passo 4
Por fim precisamos fazer o balanceamento de equações e incógnitas das nossas estruturas, já sabemos que temos 3 equações de equilíbrio, que serão mais especificadas nas próximas aulas, e também sabemos que rótulas internas a estrutura geram mais 1 equação quando possuem apenas duas barras nela. E quanto aos apoios sabemos que dobradiças geram 2 incógnitas
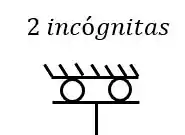
que apoios do primeiro gênero apenas 1 incógnita

E que os engastes geram 3 incógnitas
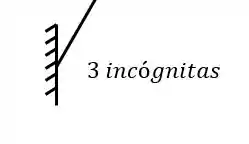
Dessa forma olhando cada estrutura separadamente, teremos que
- Primeira estrutura
- Segunda estrutura
- Terceira estrutura

Vemos que ela possui 1 apoio de engaste, ou, do terceiro gênero, logo, possui 3 incógnitas. Como temos 3 incógnitas e 3 equações, sabemos que a nossa estrutura foi dividida corretamente.

Vemos que ela possui 3 apoios do primeiro gênero, logo, possui 3 incógnitas, já que cada apoio gera uma incógnita. Como temos 3 incógnitas e 3 equações, sabemos que a nossa estrutura foi dividida corretamente.
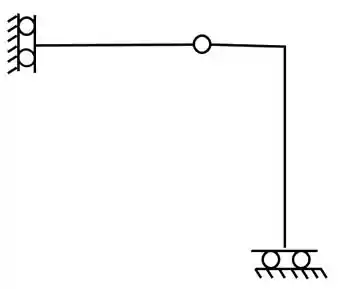
Vemos que ela possui 2 apoios do tipo dobradiça, logo, possui 4 incógnitas, já que cada apoio gera duas incógnitas. Sabemos que uma rótula na estrutura, tendo duas barras nela, gera mais 1 equação, logo, temos dessa vez, 4 equações para essa estrutura. Como temos 4 incógnitas e 4 equações, sabemos que a nossa estrutura foi dividida corretamente.
E dessa forma ao invés de resolvermos uma estrutura muito complexa de grelhas, resolveríamos três mais simples.
Resposta
A separação da grelha será