Teoria
Introdução
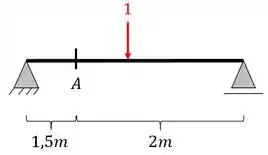
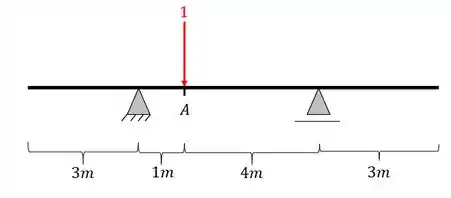
Até agora vimos que podemos encontrar os momentos fletores, cortantes e normais das nossas estruturas, mas, em alguns casos, desejamos descobrir qual a pior situação de momento fletor que podemos submeter a nossa estrutura no ponto A, por exemplo, imagine que temos a seguinte viga, e o seguinte carregamento
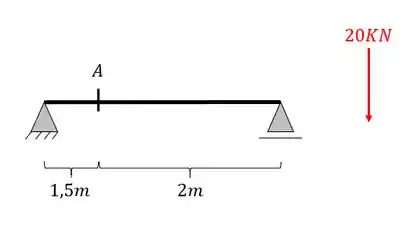
Em que ponto da barra teremos que aplicar a carga de 20KN para termos o pior momento fletor na seção A?
Ai que entra o nosso conceito de linha de influência.
Linha de influência
O conceito de influência é o seguinte:
“Devemos passar por toda a nossa viga uma carga unitária, e anotar todos os valores de momentos que teremos na nossa seção A para cada posição que colocarmos a carga unitária.”

Pode parecer meio complexo, mas é bem simples, vamos ver um passo a passo para o nosso exemplo e a partir dele vamos ver que é bem simples calcular a linha de influência.
Passo 1: Determinar pontos para colocarmos a Carga unitária
O primeiro passo é bem simples, vamos pegar ponto chaves da nossa viga, que geralmente são
- Apoios
- Extremidades de balanços
- Seção analisada
- Meios do vão
- Rótulas
No nosso caso teremos os seguintes pontos chaves
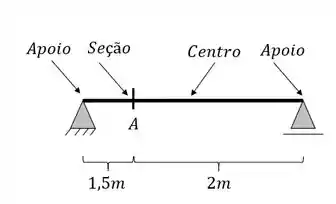
Ou seja, em todos os pontos marcados deveremos por uma carga unitária e definir o valor no Momento fletor na seção A, que é exatamente o nosso objetivo.
Passo 2: Desenhar para cada posição o diagrama de momentos fletores relacionados a carga unitária.
Agora vem a parte mais chata. Para cada carga unitária iremos desenhar um diagrama e anotaremos o valor do momento fletor em A. Vale lembrar que nas aulas de vigas simples e esforços internos em vigas, dos assuntos vigas e momento fletor, ensinamos todo o passo a passo para determinarmos os diagramas da nossa viga, por isso, aqui apresentaremos direto os diagramas e seus valores
- Primeiro apoio
- Seção
- Centro
- Se aplicarmos uma carga unitária no ponto teremos um momento fletor na posição da seção A igual a , ou seja, na posição 1,5 que é onde a seção A está.
- Ou seja, cada ordenada da nossa linha de influencia representa o momento fletor na nossa seção A quando aplicamos uma carga unitária naquela posição em que está a ordenada.
Quando aplicamos a carga unitária no primeiro apoio temos que
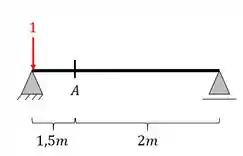

Logo, podemos anotar que para temos . Vale ressaltar aqui que pela simetria, quando aplicarmos a Carga unitária no último apoio, também teremos o diagrama igual a zero, e dessa forma poderemos dizer que temos .
Aplicando agora a carga unitária na nossa seção teremos que
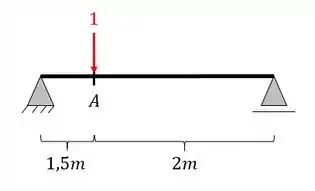
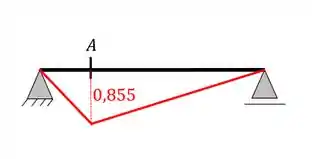
Ou seja, nesse caso podemos dizer que temos
Aplicando agora a carga unitária no centro da viga teremos que

Ou seja, nesse caso podemos dizer que temos
Passo 3: Juntar os valores em um único desenho e fazer a Linha de Influência.
Agora entra o pulo do gato. Veja que pra cada posição temos um valor de momento para a nossa seção A, quando andamos coma carga unitária por toda a viga. Se fizermos o desenho dos pontos, juntamente com as suas coordenas teremos
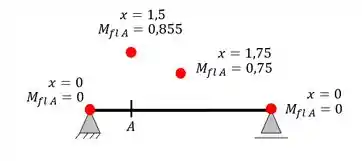
OBS:. O Sinal é arbitrado por cada professor, alguns professores utilizam valores positivos para cima e outros utilizam positivo para baixo, no nosso exemplo arbitramos o positivo para cima, mas em outros caso irei arbitrar o positivo pra baixo apenas pra mostrar que independente do sentido escolhido a resposta sempre deve ser a mesma, mas pode ficar tranquilo que sempre vou estar lembrando você disso.
Mas voltando, temos pontos pois fizemos a nossa linha a partir de pontos chaves, mas lembre-se que fizemos a nossa carga unitária passar em cada milimetro da barra, ou seja, a nossa linha de influencia será apenas ligar os pontos, passando a ter então
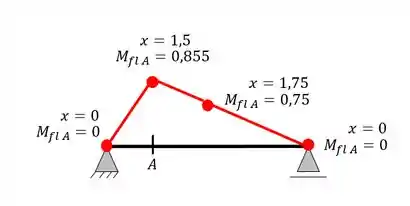
E ai é que entra uma conceito de suma importância.
“A LINHA DE INFLUÊNCIA NÃO É UM DIAGRAMA DE ESFORÇOS”
Sério, toma muito cuidado com isso, esse diagrama que desenhamos significa o seguinte:
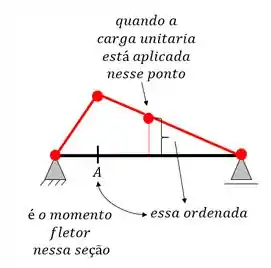
Mas beleza, porque fizemos isso? Pois tínhamos um carregamento de 20KN para aplicar na nossa barra e assim ter o pior momento na seção A com aquele carregamento, vamos fazer isso então.
Passo 4: Aplicar o carregamento no maior valor de ordenada da linha de influência.
Aplicamos no maior valor para podermos ter o pior momento fletor da nossa seção com aquele carregamento, e para descobrirmos o pior momento basta multiplicar o nosso carregamento pela ordenada daquela posição, no nosso exemplo teríamos
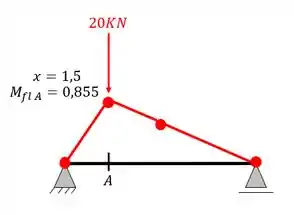
Assim sendo, o nosso pior momento na seção A será
No caso de cargas distribuídas temos que fazer a área da linha de influência abaixo do carregamento, multiplicado pelo próprio carregamento, por exemplo
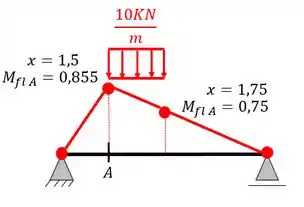
Veja que abaixo do carregamento temos um trapézio, basta calcular a área do trapézio e multiplicar pela carga distribuída que temos, e assim teremos que
Se por acaso ele pedisse para posicionar tanto a carga distribuída quanto a concentrada, bastaria apenas calcular cada uma separadamente e somar os seus valores, ou seja, a nossa situação seria
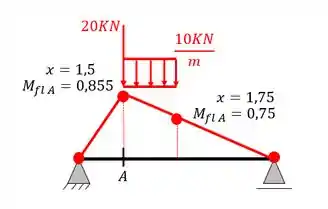
Logo o nosso pior momento a seção A, nesse caso seria
Onde mais podem me pedir linha de influência?
No nosso exemplo, apenas entendemos o conceito de linha de influência, que se resume em, passar uma carga unitária por toda a viga, e pegar os valores de cada esforço na nossa seção, para cada posição da carga unitária, mas além do momento fletor, que vimos no nosso exemplo, nos temos
- Linha de influência do cortante
- Linha de influência do cortante a esquerda e direita do apoio
- Linha de influência de apoio
- Linha de Influência de balanço
- Linha de influência de viga Gerber
Dentre muitos outros exemplos, porém, vale deixar claro o seguinte:
Independente da linha de influencia que seja pedida, o passo a passo é o mesmo, ou seja, o conceito é o mesmo, que em resumo é o seguinte
- Passo 1: definir os pontos chaves
- Passo 2: calcular o esforço pedido em uma determinada seção, usando uma carga unitária em cada ponto chave. (o esforço pode ser Normal, Cortante, Fletor, Reação de apoio...)
- Passo 3: desenhar a linha de influência com os valores do passo 2
- Passo 4: colocar o carregamento na situação que dê o maior esforço na seção calculada
- Obs:. Como as nossas estruturas sempre serão isostáticas, a nossa linha de influência sempre será composta por retas, então nunca use curvas na linha de influência.
Entendido o conceito e onde ele pode cair, vamos partir para os exercícios, para não termos mais problema com esse tipo de questão.
Bora gabaritar a prova? Bora fazer exercício então!!!

Passo 1: Determinar pontos para colocarmos a Carga unitária
Passo 2: Desenhar para cada posição o diagrama de momentos fletores relacionados a carga unitária.
Passo 3: Juntar os valores em um único desenho e fazer a Linha de Influência.
Passo 4: Aplicar o carregamento no maior valor de ordenada da linha de influência.
Onde mais podem me pedir linha de influência?
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine a linha de influência de cortantes da seção A abaixo pelo método da carga unitária.
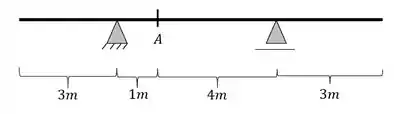
Passo 1
Sabemos que temos sempre que seguir um passo a passo para solucionar o nosso problema, e nesse caso o nosso passo a passo será:
- Primeiro devemos separar pontos chaves para calcularmos o valor do nosso cortante na seção A. Devemos lembrar que pontos chaves são extremidades, apoios, meios de vão, e outros pontos que devemos considerar de suma importância.
- Em seguida, em cada ponto chave colocamos a carga unitária, claro, lembrando de fazer uma de cada vez, e com a carga unitária posicionada calculamos as reações de apoio e cortantes na seção A.
- Por fim, teremos uma sequência de valores de cortante para nossa seção A, marcamos esses pontos na nossa viga e ligamos eles através de retas. Feito isso teremos exatamente a nossa linha de influência.
Entendido o processo de construção, vamos colocá-lo em pratica.
Passo 2
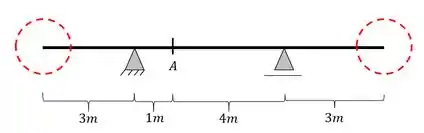
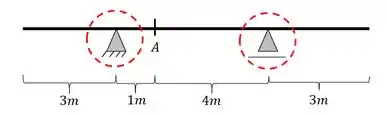
Como vimos, a primeira coisa que devemos fazer é marcar os pontos chaves de cálculo da nossa viga. Sabemos que devemos marcar esses pontos chaves da seguinte maneira
- Extremidades
- Apoios
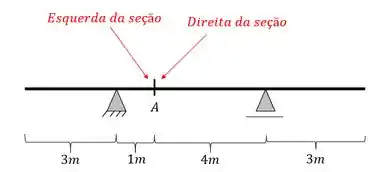
- Seção Calculada (Direita/ Esquerda)
- Cortante na seção A devido a carga unitária na extremidade mais a esquerda
- Cortante na seção A devido a carga unitária no apoio mais á esquerda
- Cortante na seção A devido a carga unitária à esquerda da seção A
- Cortante na seção A devido a carga unitária à direita da seção A
- Cortante na seção A devido a carga unitária no apoio mais a direita
- Cortante na seção A devido a carga unitária na extremidade mais a Direita
feito isso vamos ao próximo passo.
Passo 3
Esse passo se refere ao cálculo do cortante na seção A. Sabemos que em cada ponto chave do passo anterior devemos colocar uma carga unitária. Dessa forma teremos os seguintes valores de cortantes na nossa seção A da viga.
Primeiro colocamos a nossa carga unitária posicionada
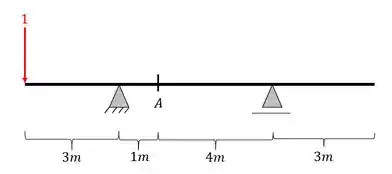
Depois calculamos as reações de apoio da nossa viga
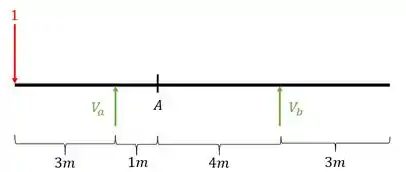
Usando as fórmulas de equilíbrio teremos que
Como deu negativo basta invertermos o nosso vetor
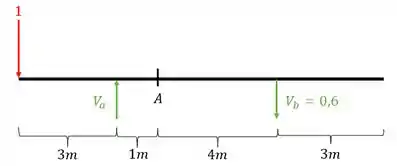
Calculando teremos que
Cortando a parte esquerda da nossa viga na seção A teremos que
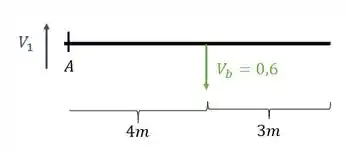
Logo o cortante que equilibra a viga será
Positivo pois sabemos que quando estamos vindo pela esquerda com vetor cortante pra cima o sinal no nosso cortante é positivo. Com isso calculamos o valor do nosso cortante na seção A quando temos uma carga unitária na extremidade. Vamos ao próximo ponto chave.
Passo 4
Primeiro colocamos a nossa carga unitária posicionada
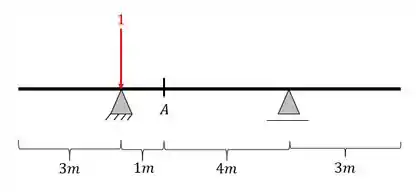
Depois calculamos as reações de apoio da nossa viga
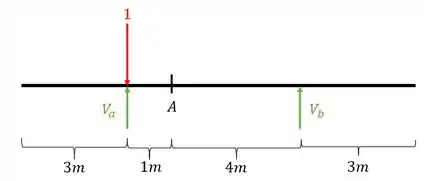
Usando as fórmulas de equilíbrio teremos que
Logo para teremos que
Cortando a parte esquerda da nossa viga na seção A teremos que
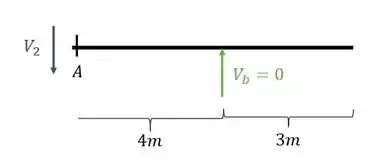
Logo o cortante que equilibra a viga será
Com isso calculamos o valor do nosso cortante na seção A quando temos uma carga unitária no apoio mais à esquerda. Vamos ao próximo ponto chave.
Passo 5
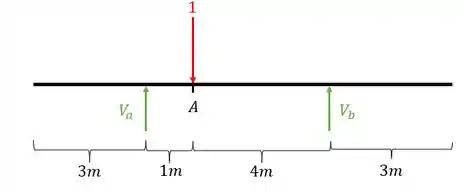
Primeiro colocamos a nossa carga unitária posicionada
Depois calculamos as reações de apoio da nossa viga
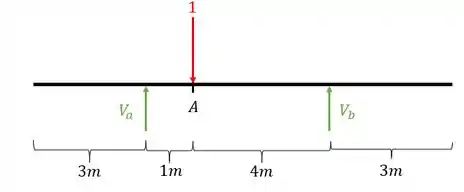
Usando as fórmulas de equilíbrio teremos que
Logo para teremos que
Cortando a parte esquerda da nossa viga na seção A, e lembrando que nesse caso a nossa carga esta um pouquinho para esquerda, o que fará ela sumir, teremos que
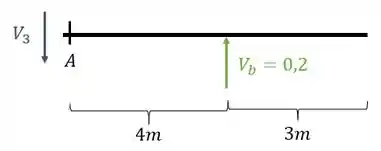
Logo o cortante que equilibra a viga será
É negativo nesse caso porque vindo pela esquerda o nosso cortante está para baixo, o que caracteriza ele como um cortante negativo. Com isso calculamos o valor do nosso cortante na seção A quando temos uma carga unitária na seção A mais à esquerda. Vamos ao próximo ponto chave.
Passo 6
Primeiro colocamos a nossa carga unitária posicionada
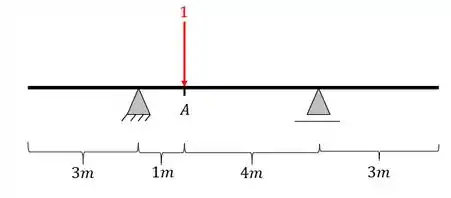
Depois calculamos as reações de apoio da nossa viga
Usando as fórmulas de equilíbrio teremos que
Logo para teremos que
Cortando a parte esquerda da nossa viga na seção A, e lembrando que nesse caso a nossa carga está um pouquinho para direita, o mantém ela, teremos que
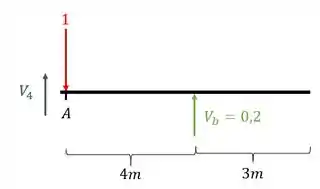
Logo o cortante que equilibra a viga será
Positivo pois sabemos que quando estamos vindo pela esquerda com vetor cortante pra cima o sinal no nosso cortante é positivo. Com isso calculamos o valor do nosso cortante na seção A quando temos uma carga unitária a direita da seção A. Vamos ao próximo ponto chave.
Passo 7
Primeiro colocamos a nossa carga unitária posicionada
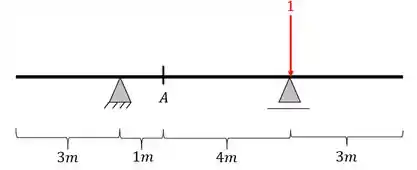
Depois calculamos as reações de apoio da nossa viga
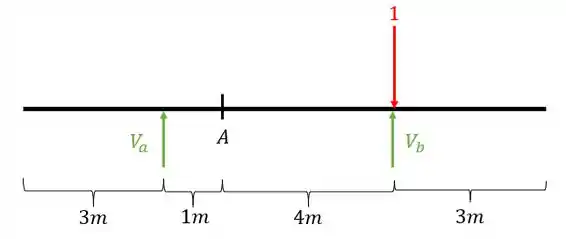
Usando as fórmulas de equilíbrio teremos que
Logo para teremos que
Cortando a parte esquerda da nossa viga na seção A teremos que
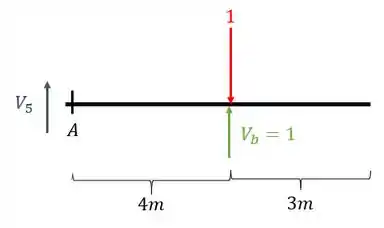
Logo o cortante que equilibra a viga será
Com isso calculamos o valor do nosso cortante na seção A quando temos uma carga unitária no apoio mais à direita. Vamos ao próximo ponto chave.
Passo 8
Primeiro colocamos a nossa carga unitária posicionada
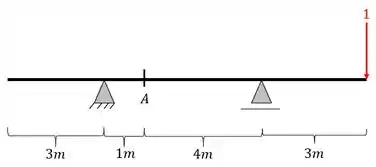
Depois calculamos as reações de apoio da nossa viga
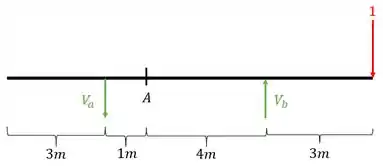
Usando as fórmulas de equilíbrio teremos que
Calculando teremos que
Cortando a parte esquerda da nossa viga na seção A teremos que
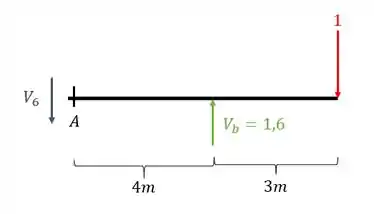
Logo o cortante que equilibra a viga será
Apesar de matematicamente o valor ser positivo, ele aparece como negativo pois sempre que o nosso cortante vem para baixo pela esquerda seu sinal é negativo, por isso, temos que nesse caso o nosso cortante é negativo. Com isso calculamos o valor do nosso cortante na seção A quando temos uma carga unitária na extremidade.
Passo 3
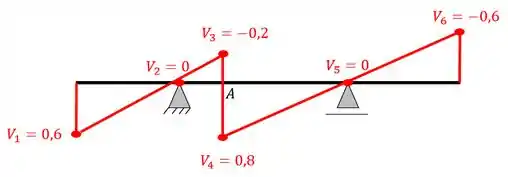
Vemos que depois de calcularmos os pontos chaves, devemos marca-los na viga e ligarmos os pontos através de retas, dessa forma teremos que
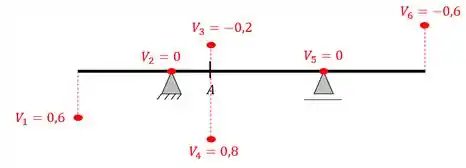
Perceba que na linha de influência, os valores positivos ficam na parte de baixo e os negativos na parte de cima. Alguns professores usam os sinais normais (positivo em cima e negativo em baixo) mas a maioria dos livros usam o esquema de sinais mostrados acima, mas os sinais não têm importância se você sempre usar a mesma regra, basta apenas não misturar.
Com isso, ligando os pontos, a nossa linha de influência será.
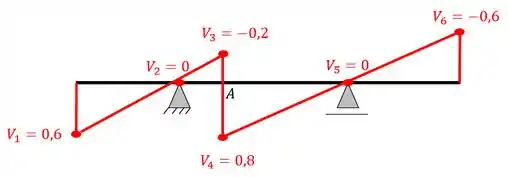
Resposta
Linha de influência de cortantes na seção A
Exercício Resolvido #2
Elaboração Própria
Determine a linha de influência de reações de apoio do apoio A abaixo pelo método da carga unitária.
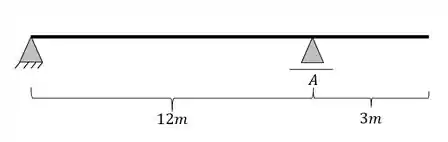
Passo 1
Sabemos que temos sempre que seguir um passo a passo para solucionar o nosso problema, e nesse caso o nosso passo a passo será:
- Primeiro devemos separar pontos chaves para calcularmos o valor das nossas reações no apoio A. Devemos lembrar que pontos chaves são extremidades, apoios, meios de vão, e outros pontos que devemos considerar de suma importância.
- Em seguida, em cada ponto chave colocamos a carga unitária, claro, lembrando de fazer uma de cada vez, e com a carga unitária posicionada calculamos as reações de apoio.
- Por fim, teremos uma sequência de valores de reações do nosso apoio A, marcamos esses pontos na nossa viga e ligamos eles através de retas. Feito isso teremos exatamente a nossa linha de influência.
Entendido o processo de construção, vamos colocá-lo em pratica.
Passo 2
Como vimos, a primeira coisa que devemos fazer é marcar os pontos chaves de cálculo da nossa viga. Sabemos que devemos marcar esses pontos chaves da seguinte maneira
- Extremidades
- Apoios
- Meio do vão
- Reação do apoio A quando colocamos uma carga unitária na extremidade mais a direita da nossa viga
- Reação do apoio A quando colocamos uma carga unitária no apoio mais à direita (o próprio apoio A)
- Reação do apoio A quando colocamos a nossa carga unitária no meio do vão
- Reação do apoio A quando colocamos a nossa carga unitária sobre o apoio mais a esquerda (o apoio B)
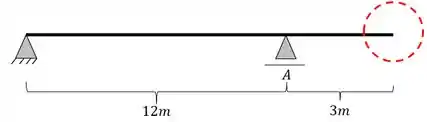
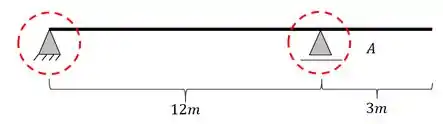
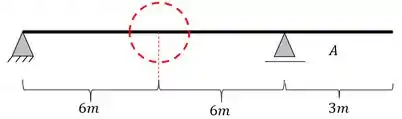
feito isso vamos ao próximo passo.
Passo 3
Esse passo se refere ao cálculo das reações de apoio A. Sabemos que em cada ponto chave do passo anterior devemos colocar uma carga unitária. Dessa forma teremos os seguintes valores de reação no nosso apoio A da viga.
Primeiro colocamos a nossa carga unitária posicionada
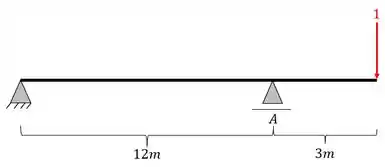
Depois calculamos as reações de apoio da nossa viga
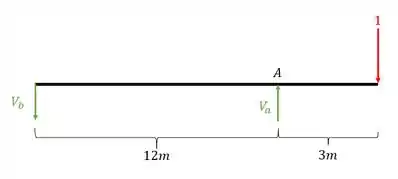
Usando as fórmulas de equilíbrio teremos que
Calculando teremos que
Logo a reação do apoio A quando colocamos uma carga na extremidade mais a direita é a que acabamos de calcular.
Passo 4
Primeiro colocamos a nossa carga unitária posicionada
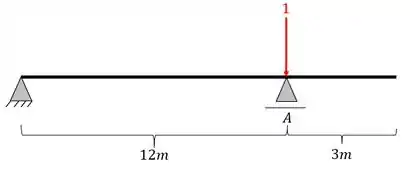
Depois calculamos as reações de apoio da nossa viga
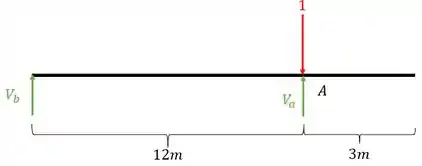
Usando as fórmulas de equilíbrio teremos que
Logo para teremos que
E essa é a reação do nosso apoio A quando colocamos a carga unitária sobre ele.
Passo 5
Primeiro colocamos a nossa carga unitária posicionada
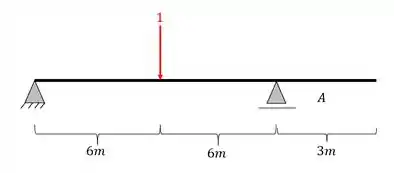
Depois calculamos as reações de apoio da nossa viga
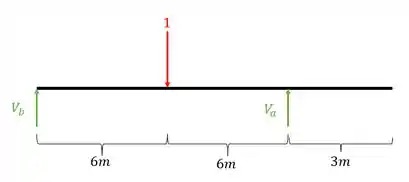
Usando as fórmulas de equilíbrio teremos que
Logo para teremos que
E essa é a reação do nosso apoio A quando colocamos a carga unitária no vão central.
Passo 6
Primeiro colocamos a nossa carga unitária posicionada
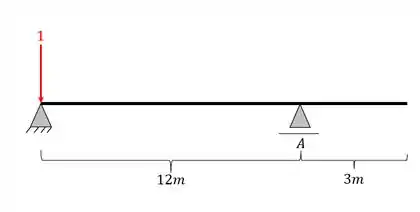
Depois calculamos as reações de apoio da nossa viga
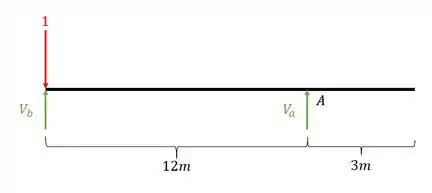
Usando as fórmulas de equilíbrio teremos que
Logo para teremos que
E essa é a reação do nosso apoio A quando colocamos a carga unitária no apoio mais a esquerda, ou seja, o apoio B.
Passo 3
Vemos que depois de calcularmos os pontos chaves, devemos marca-los na viga e ligarmos os pontos através de retas, dessa forma teremos que
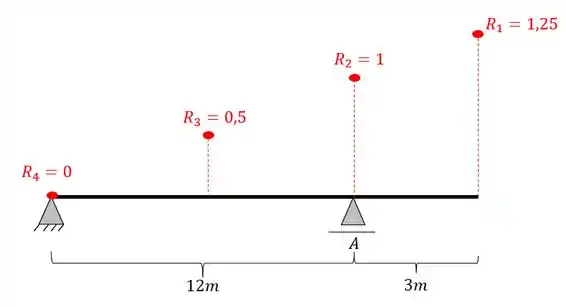
ligando os pontos, a nossa linha de influência será.
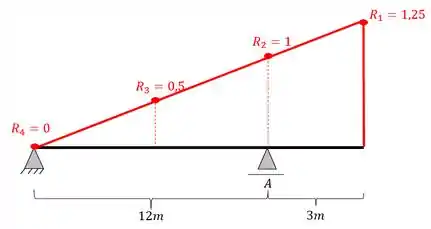
Resposta
Linha de influência de reações de apoio do apoio A
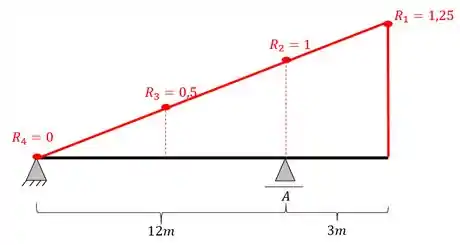
Exercício Resolvido #3
Elaboração Própria
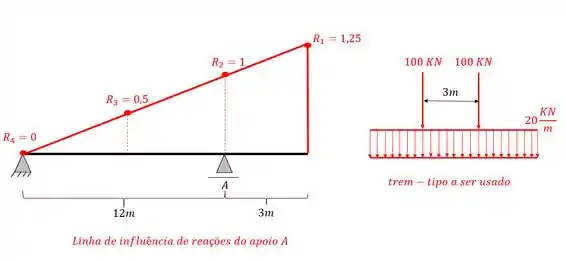
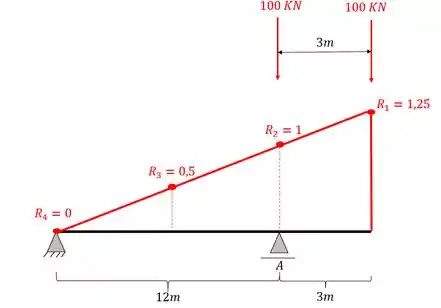
Dada a linha de influência de reação de apoio do apoio A abaixo junto com seu trem-tipo, determine qual será a máxima reação de apoio a agir na nossa viga no apoio A.
Passo 1
Já sabemos que tudo que vamos fazer é necessário o uso do nosso passo a passo para sabermos como resolver esse tipo de questão, e o nosso passo a passo é,
- Primeiro devemos posicionar o nosso trem tipo na nossa linha de influência de forma que o carregamento distribuído sempre seja favorável ao que o enunciado pede e o carregamento concentrado fique sempre na maior ordenada da linha de influência, de forma a ser favorável também ao que o enunciado pede.
- Posicionado o carregamento distribuído, devemos calcular a área abaixo da região que o carregamento distribuído está e multiplicar essa área pelo carregamento distribuído.
- Posicionado o carregamento concentrado, apenas multiplicaremos a ordenada que está logo abaixo do carregamento concentrado pelo carregamento concentrado.
- Calculado todos esses valores, somamos ou subtraímos, dependendo do sinal, os valores encontrados, o resultado final será exatamente a maior reação que o nosso apoio A estará sofrendo na presença do nosso trem tipo.
Entendido o nosso passo a passo, vamos a aplicação no nosso problema.
Passo 2
Como vemos, o primeiro passo consiste em posicionarmos o trem tipo na nossa linha de influência. Como a nossa linha de influência está totalmente acima do eixo da viga, podemos posicionar a nossa carga distribuída por toda a extensão da viga e da linha de influência, dessa forma o posicionamento do nosso carregamento distribuído será
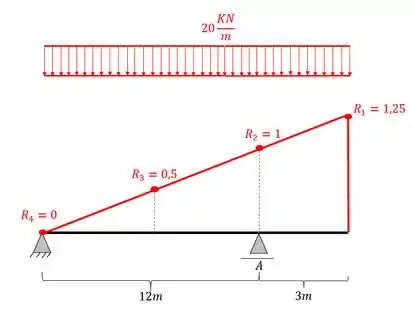
Já o carregamento concentrado deve ficar posicionado nas maiores ordenadas da nossa linha de influência, mas sempre respeitando a distância imposta pelo trem tipo, dessa forma teremos que
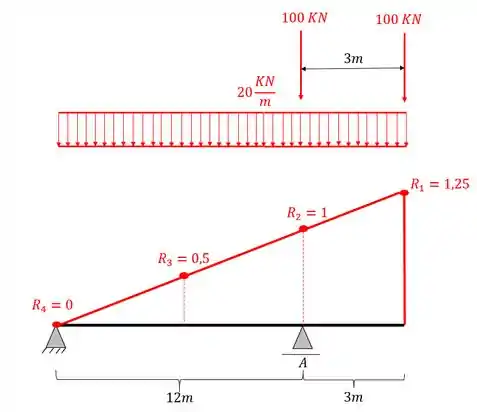
E assim posicionamos o nosso trem tipo com a nossa linha de influência.
Passo 3
Vemos que o segundo passo consiste em
Podemos ver que a região abaixo da carga distribuída é um triangulo com as seguintes dimensões
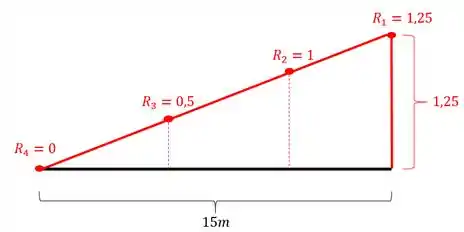
Logo teremos que
E sabemos que a carga distribuída é
Dessa forma teremos que
Passo 4
O terceiro passo é relacionada a carga concentrada, em que sabemos que devemos multiplicar a carga concentrada pela ordenada que ela se encontra, dessa forma teremos que
Fazendo a conta teremos que
Passo 5
Por fim, o último passo consiste em somarmos as reações encontradas, e assim determinar a máxima reação que ocorrerá no nosso apoio A quando aplicarmos o trem tipo mostrado, dessa forma teremos que
Que é exatamente o pior carregamento que o nosso apoio A irá sofrer se posicionássemos o trem tipo como vimos acima,
Resposta
Exercício Resolvido #4
Elaboração Própria
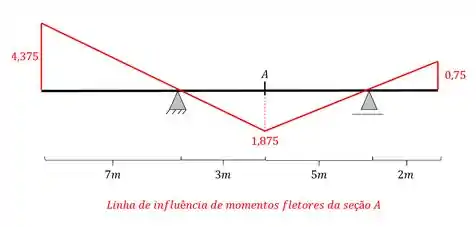
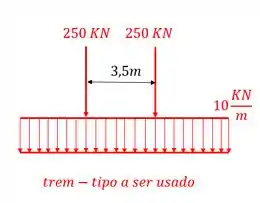
Dada a linha de influência de momentos da seção A abaixo junto com seu trem-tipo, determine qual será o máximo momento negativo (traciona as fibras na parte de cima da seção) a agir na nossa viga na seção A.
Passo 1
Já sabemos que tudo que vamos fazer é necessário o uso do nosso passo a passo para sabermos como resolver esse tipo de questão, e o nosso passo a passo é,
- Primeiro devemos posicionar o nosso trem tipo na nossa linha de influência de forma que o carregamento distribuído sempre seja favorável ao que o enunciado pede e o carregamento concentrado fique sempre na maior ordenada da linha de influência, de forma a ser favorável também ao que o enunciado pede.
- Posicionado o carregamento distribuído, devemos calcular a área abaixo da região que o carregamento distribuído está e multiplicar essa área pelo carregamento distribuído.
- Posicionado o carregamento concentrado, apenas multiplicaremos a ordenada que está logo abaixo do carregamento concentrado pelo carregamento concentrado.
- Calculado todos esses valores, somamos ou subtraímos, dependendo do sinal, os valores encontrados, o resultado final será exatamente o maior momento que a nossa seção A estará sofrendo na presença do nosso trem tipo.
Entendido o nosso passo a passo, vamos a aplicação no nosso problema.
Passo 2
Como vemos, o primeiro passo consiste em posicionarmos o trem tipo na nossa linha de influência. Como a nossa linha de influência possui áreas acima do eixo da viga e abaixo do eixo da viga, precisamos lembrar que os momentos negativos, usualmente, têm suas ordenadas posicionadas acima do eixo da viga, ou seja, tracionando as fibras da parte de cima. podemos posicionar a nossa carga distribuída em todas as áreas que estiverem acima do eixo da nossa viga, dessa forma o posicionamento do nosso carregamento distribuído será
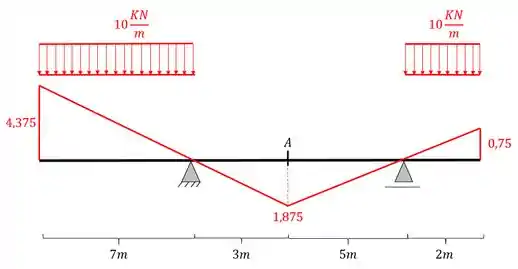
Já o carregamento concentrado deve ficar posicionado nas maiores ordenadas da nossa linha de influência, mas sempre respeitando a distância imposta pelo trem tipo, dessa forma teremos que
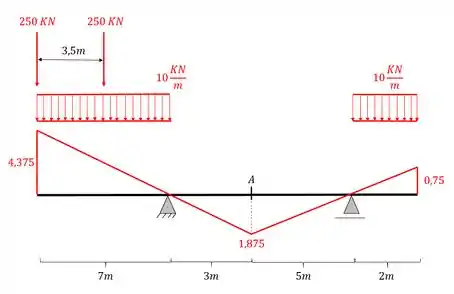
E perceba o seguinte, apesar de no nosso lado direito termos um máximo, só podemos posicionar o nosso trem tipo concentrado em um lugar, e ainda temos que respeitar a distância, como o lado esquerdo tem o maior valor, posicionamos o concentrado apenas desse lado.
E assim posicionamos o nosso trem tipo com a nossa linha de influência.
Passo 3
Vemos que o segundo passo consiste em
Podemos ver que a região abaixo da carga distribuída são dois triângulos com as seguintes dimensões
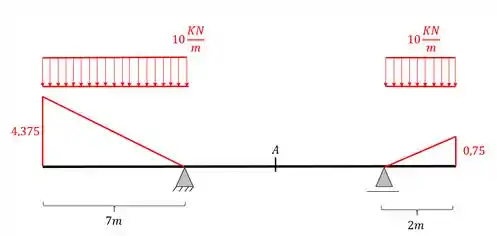
Logo teremos que
E sabemos que a carga distribuída é
Dessa forma teremos que
Passo 4
O terceiro passo é relacionada a carga concentrada, em que sabemos que devemos multiplicar a carga concentrada pela ordenada que ela se encontra, dessa forma teremos que
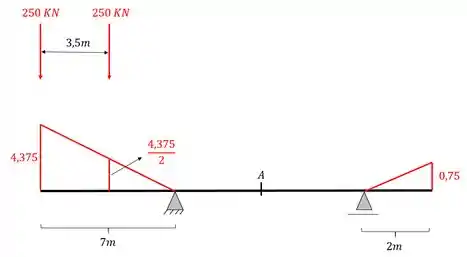
Fazendo a conta teremos que
Passo 5
Por fim, o último passo consiste em somarmos os momentos encontradas, e assim determinar o máximo momento negativo que ocorrerá na nossa seção A quando aplicarmos o trem tipo mostrado, dessa forma teremos que
Que é exatamente o pior carregamento que a nossa seção A irá sofrer se posicionássemos o trem tipo como vimos acima,