Linha de Influência Cortante e Momento- Método Gráfico
Produzido por Pablo RicardoTeoria
A linha de influência nos dá o pior cenário possível de uma carga em uma viga! Se liga na figura abaixo:

Imagina que você queira saber em qual posição a gente pode colocar uma carga concentrada, na viga acima, de modo que ela resulte no pior momento em
Hoje a gente vai focar no método gráfico para calcular as linhas de Influência cortante e de momento fletor, se você quiser entender um pouco mais a fundo o que é linha de influência, dá uma clicada aqui e depois volta pra cá! 🏃🏃🏃
Linha de Influência: Momento Fletor
Vamos começar aprendendo como calcular a Linha de Influência do Momento Fletor, usando o método gráfico, que é a forma mais prática de fazer esse cálculo!
Para isso liga nessa viga abaixo:
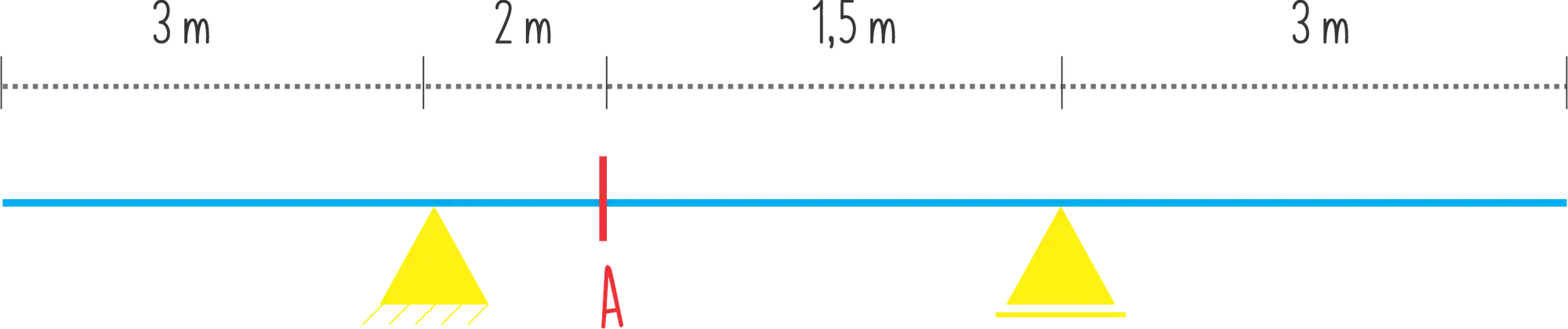
Vamos calcular o momento fletor dela!
Passo 1: Rebater as Distâncias Apoio/Secção A até os apoios
Falando assim parece confuso, mas se liga nessa imagem:
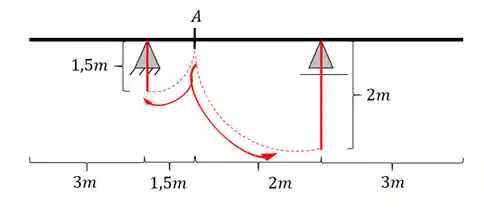
Passo 2: Ligar a extremidade de cada trecho rebatido até os apoios
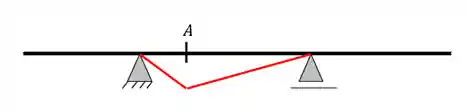
Fazemos um x na nossa estrutura, assim:
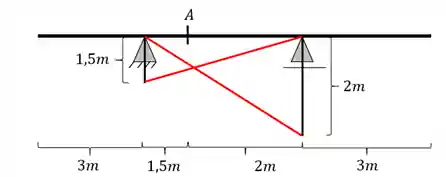
Caso a nossa estrutura não tivesse balanço, seria necessário apenas apagar as linhas de forma, deixando apenas do trecho de encontro pra cima, por exemplo:
Você também pode conferir esse conteúdo em vídeo:
Passo 3: Estender as linhas do apoio até o final do balanço
Com isso teremos que:
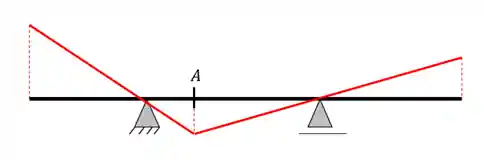
Pronto! Essa é a nossa linha de influência de momento, para descobrir os valores dela basta calcular o valor do momento na seção A quando colocarmos uma carga unitária nas extremidades!
Linha de Influência: Momento Cortante
Pra aprendermos o método gráfico para cortantes vamos continuar com a viga do exemplo anterior!
Passo 1: Esticar uma reta de valor unitário nos apoios
No apoio da direita esticamos para cima, e no da esquerda para baixo, como podemos ver na figura abaixo:
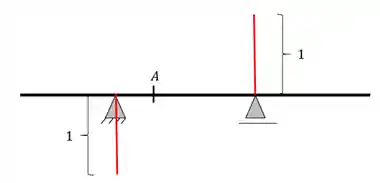
Passo 2: Ligar a extremidade de cada linha estendida ao apoio contrário
Aqui precisamos ter cuidado para que essas retas sejam paralelas. Com isso teremos:
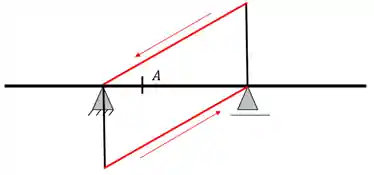
Passo 3: Esticar as retas paralelas até o fim dos balanços
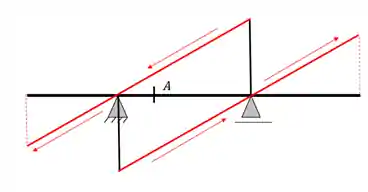
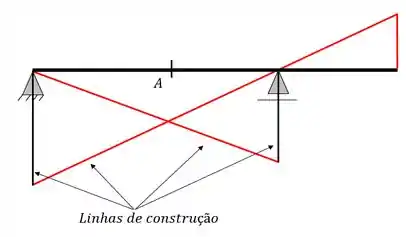
Passo 4: Ligar as retas paralelas por uma reta transversal que passe pela seção pedida.
Dessa forma temos:
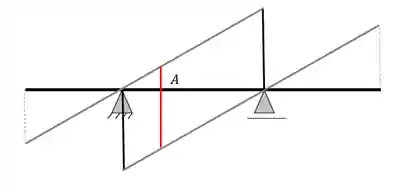
Agora só precisamos tirar as linhas de construção e esta pronto:
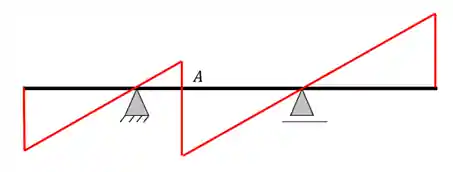
Agora vamos praticar com exercícios?!
Linha de Influência: Momento Cortante
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine a linha de influência de momentos fletores para a seção A da viga abaixo pelo método gráfico. Calcule também os principais valores dessa linha de influência.
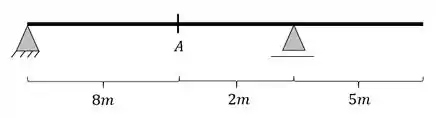
Passo 1
Já sabemos que o passo a passo que iremos seguir é o seguinte:
- Primeiro marcamos a nossa seção na viga
- Depois pegamos as distâncias de cada apoio até a seção e rebatemos elas como raios pra baixo dos apoios
- Em seguida ligamos as pontas dessas barras em baixo dos apoios no apoio contrário
- E por fim, se houver um balanço nós prolongamos essas barras até o balanço
- Feito tudo isso teremos a nossa linha de influência, e a única coisa que irá ficar faltando será calcular os valores principais dessas linhas, que iremos usar regra de 3 para calcularmos.
- Por fim, Apagar as linhas de construção.
Entendido tudo isso, vamos ao cálculo da nossa linha de influência.
Passo 2
Já sabemos que o primeiro passo foi feito no próprio enunciado que marcou a seção no ponto que deveríamos calcular.
Vamos então já ir para o segundo passo onde iremos rebater as distâncias até os apoios como vemos na figura abaixo.
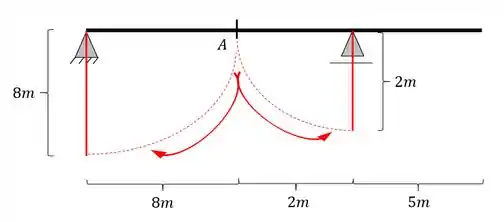
Passo 3
Como sabemos no passo a passo devemos agora ligar as extremidades de cada barra rebatida no apoio contrário, e dessa forma teremos que as linhas ficarão
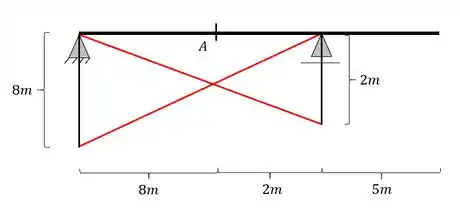
Passo 4
Para o próximo passo podemos ver que a nossa barra possui um balanço no seu lado direito, e dessa forma, prolongando essa linha até o balanço, teremos que a nossa linha de influência ficará da seguinte maneira
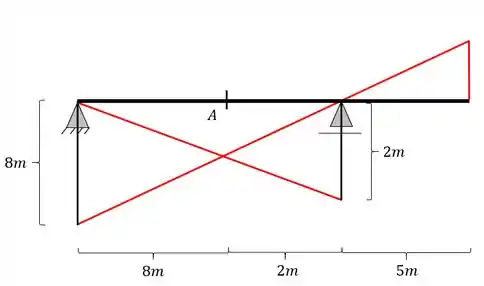
Passo 5
Agora já podemos fazer a regra de 3 levando em consideração os seguintes triangulos
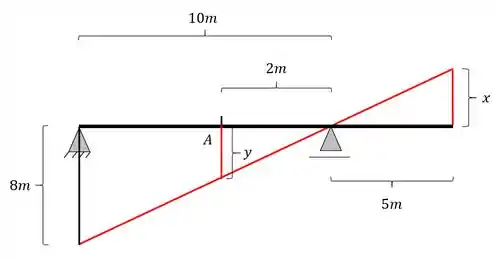
Teremos aqui a seguinte regra de 3, calculando primeiro x
Calculando agora Y, teremos o seguinte
Ou seja, calculamos os valores pertinentes da nossa linha de influência
Passo 6
Agora que já fizemos tudo basta apagarmos as nossas linhas de construção, e o que irá sobrar será exatamente a nossa linha de influência da viga
Apagando essas linhas e acrescentando os valores calculados na regra de 3 teremos a seguinte linha de influencia
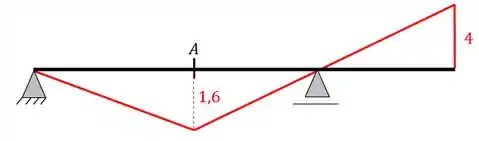
Resposta
Linha de Influência de momentos fletores na seção A por métodos gráficos
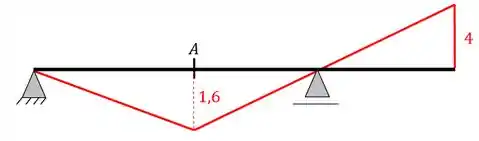
Exercício Resolvido #2
Elaboração Própria
Determine a linha de influência de momentos fletores para a seção A da viga abaixo pelo método gráfico. Calcule também os principais valores dessa linha de influência.
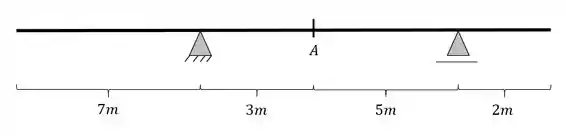
Passo 1
Já sabemos que o passo a passo que iremos seguir é o seguinte:
- Primeiro marcamos a nossa seção na viga
- Depois pegamos as distâncias de cada apoio até a seção e rebatemos elas como raios pra baixo dos apoios
- Em seguida ligamos as pontas dessas barras em baixo dos apoios no apoio contrário
- E por fim, se houver um balanço nós prolongamos essas barras até o balanço
- Feito tudo isso teremos a nossa linha de influência, e a única coisa que irá ficar faltando será calcular os valores principais dessas linhas, que iremos usar regra de 3 para calcularmos.
- Por fim, Apagar as linhas de construção.
Entendido tudo isso, vamos ao cálculo da nossa linha de influência.
Passo 2
Já sabemos que o primeiro passo foi feito no próprio enunciado que marcou a seção no ponto que deveríamos calcular.
Vamos então já ir para o segundo passo onde iremos rebater as distâncias até os apoios como vemos na figura abaixo.
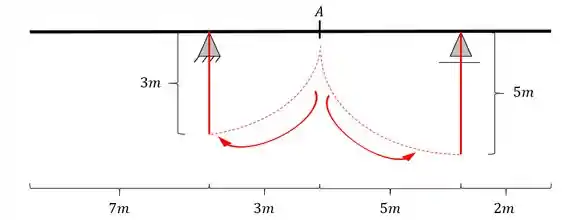
Passo 3
Como sabemos no passo a passo devemos agora ligar as extremidades de cada barra rebatida no apoio contrário, e dessa forma teremos que as linhas ficarão
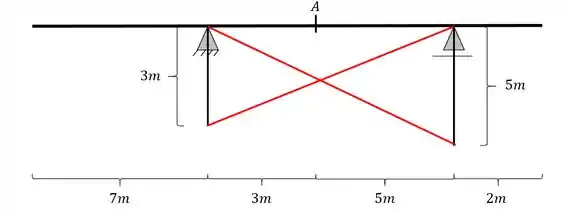
Passo 4
Para o próximo passo podemos ver que a nossa barra possui balanço em ambos os lados, e dessa forma, prolongando essa linha até o balanço, teremos que a nossa linha de influência ficará da seguinte maneira
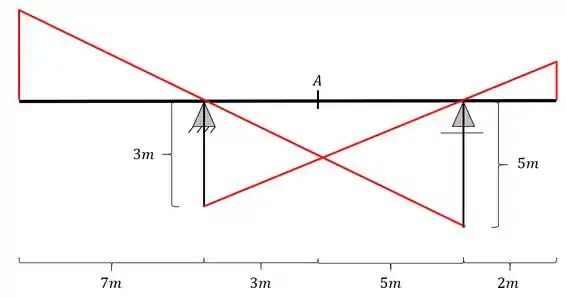
Passo 5
Agora já podemos fazer as 2 regras de 3 levando em consideração os seguintes triângulos
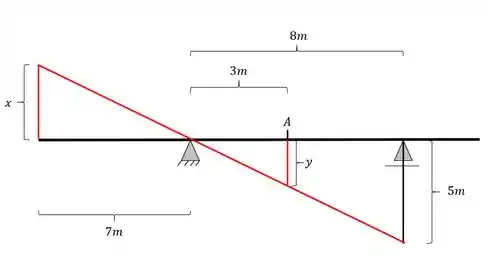
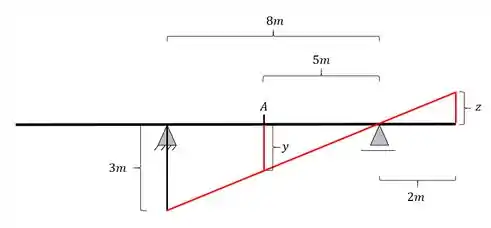
Teremos aqui a seguinte regra de 3, calculando primeiro x
Calculando agora Y, teremos o seguinte
Calculando agora Z, teremos o seguinte
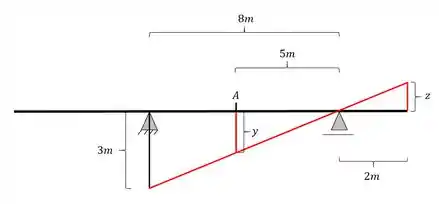
E recalculando Y para vermos se fizemos tudo certinho
Ou seja, realmente o valor de Y está certinho, e calculamos todas as regras de 3.
Passo 6
Agora que já fizemos tudo basta apagarmos as nossas linhas de construção, e o que irá sobrar será exatamente a nossa linha de influência da viga
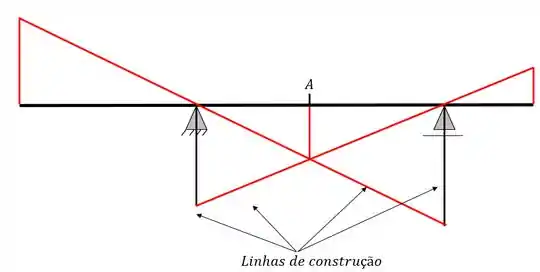
Apagando essas linhas e acrescentando os valores calculados na regra de 3 teremos a seguinte linha de influencia
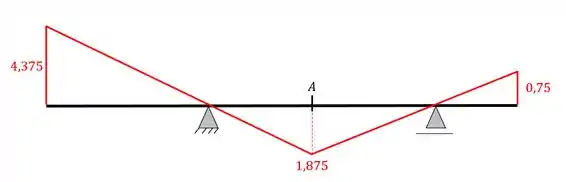
Resposta
Linha de Influência de momentos fletores na seção A por métodos gráficos
Exercício Resolvido #3
Elaboração Própria
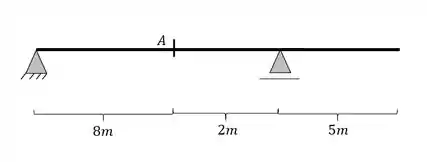
Determine a linha de influência de cortantes para a seção A da viga abaixo pelo método gráfico. Calcule também os principais valores dessa linha de influência.
Passo 1
Já sabemos que o passo a passo que iremos seguir é o seguinte:
- Primeiro marcamos a nossa seção na viga
- Depois descemos uma reta de valor unitário no apoio mais a esquerda e subimos uma reta de valor unitário no apoio mais à direita.
- Em seguida ligamos as pontas dessas retas nos apoios contrários
- Se houver um balanço nós prolongamos essas retas até o balanço
- Por fim, sabemos que devemos ligar as duas retas paralelas que chegam nos apoios por uma transversal que passa pela seção calculada.
- Feito tudo isso teremos a nossa linha de influência, e a única coisa que irá ficar faltando será calcular os valores principais dessas linhas, que iremos usar regra de 3 para calcularmos.
- Por fim, apagar as linhas de construção.
Entendido tudo isso, vamos ao cálculo da nossa linha de influência.
Passo 2
Já sabemos que o primeiro passo foi feito no próprio enunciado que marcou a seção no ponto que deveríamos calcular.
Vamos então já ir para o segundo passo onde iremos descer e subir uma reta de valor unitário em cada uns dos apoios, seguindo o sentido do passo a passo, ou seja, pra baixo na esquerda e pra cima na direita.
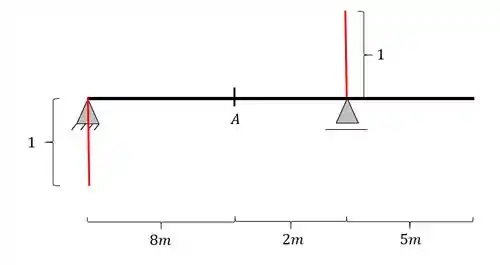
Passo 3
Como sabemos no passo a passo devemos agora ligar as extremidades de cada reta no apoio contrário, e dessa forma teremos que as linhas ficarão
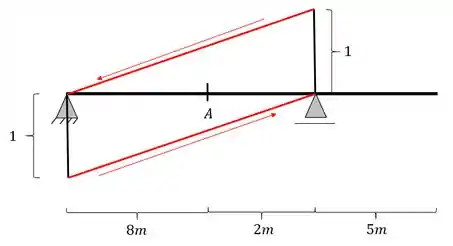
Passo 4
Para o próximo passo podemos ver que a nossa barra possui balanço em seu lado direito, e dessa forma, prolongando essa linha até o balanço, teremos que a nossa linha de influência ficará da seguinte maneira
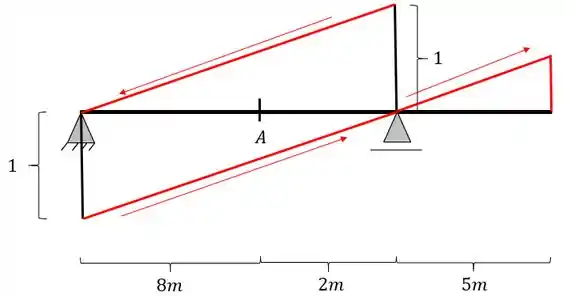
Passo 5
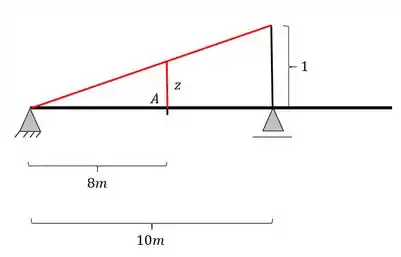
Agora iremos passar a nossa reta transversal, ligando as retas paralelas que passam nos apoios, passando pela nossa seção A que está sendo calculada, dessa forma teremos a seguinte estrutura
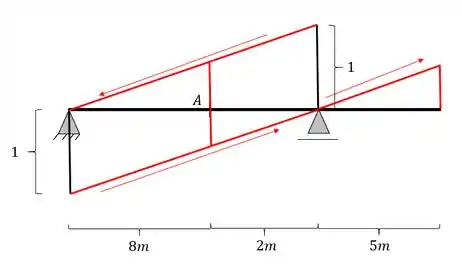
Passo 6
Agora já podemos fazer as 2 regras de 3 levando em consideração os seguintes triângulos
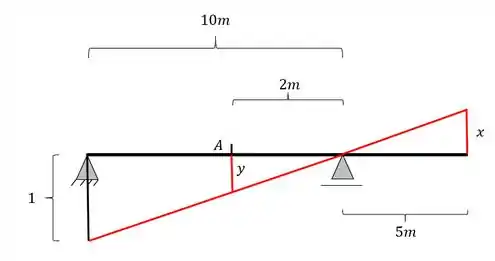
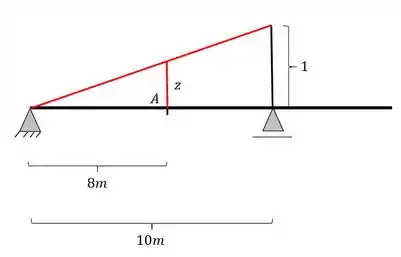
Teremos aqui a seguinte regra de 3, calculando primeiro x
Calculando agora Y, teremos o seguinte
Calculando agora Z, teremos o seguinte
E somando Y+Z teremos exatamente o valor central que tem que dar 1 já que as nossas retas são paralelas
O que comprova que de fato fizemos tudo certo já que o valor central está mantido em 1.
Passo 7
Agora que já fizemos tudo basta apagarmos as nossas linhas de construção, e o que irá sobrar será exatamente a nossa linha de influência da viga
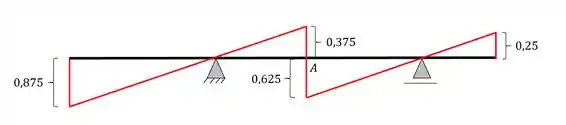
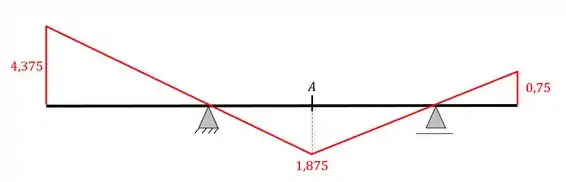
Apagando essas linhas e acrescentando os valores calculados na regra de 3 teremos a seguinte linha de influencia
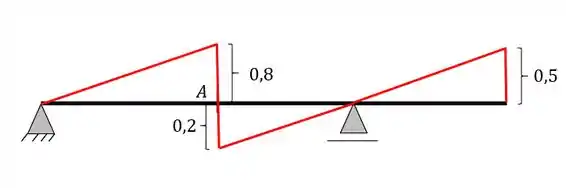
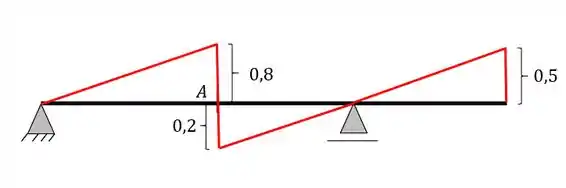
Resposta
Linha de Influência de cortantes na seção A por métodos gráficos.
Exercício Resolvido #4
Elaboração Própria
Determine a linha de influência de cortantes para a seção A da viga abaixo pelo método gráfico. Calcule também os principais valores dessa linha de influência.
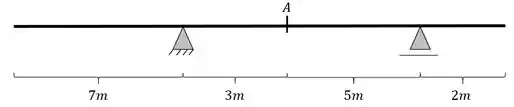
Passo 1
Já sabemos que o passo a passo que iremos seguir é o seguinte:
- Primeiro marcamos a nossa seção na viga
- Depois descemos uma reta de valor unitário no apoio mais a esquerda e subimos uma reta de valor unitário no apoio mais à direita.
- Em seguida ligamos as pontas dessas retas nos apoios contrários
- Se houver um balanço nós prolongamos essas retas até o balanço
- Por fim, sabemos que devemos ligar as duas retas paralelas que chegam nos apoios por uma transversal que passa pela seção calculada.
- Feito tudo isso teremos a nossa linha de influência, e a única coisa que irá ficar faltando será calcular os valores principais dessas linhas, que iremos usar regra de 3 para calcularmos.
- Por fim, apagar as linhas de construção.
Entendido tudo isso, vamos ao cálculo da nossa linha de influência.
Passo 2
Já sabemos que o primeiro passo foi feito no próprio enunciado que marcou a seção no ponto que deveríamos calcular.
Vamos então já ir para o segundo passo onde iremos descer e subir uma reta de valor unitário em cada uns dos apoios, seguindo o sentido do passo a passo, ou seja, pra baixo na esquerda e pra cima na direita.
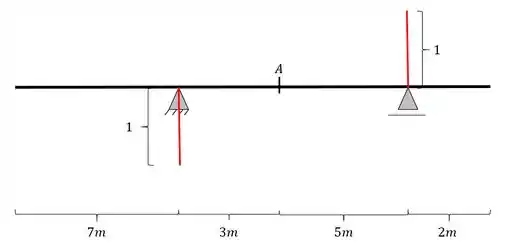
Passo 3
Como sabemos no passo a passo devemos agora ligar as extremidades de cada reta no apoio contrário, e dessa forma teremos que as linhas ficarão
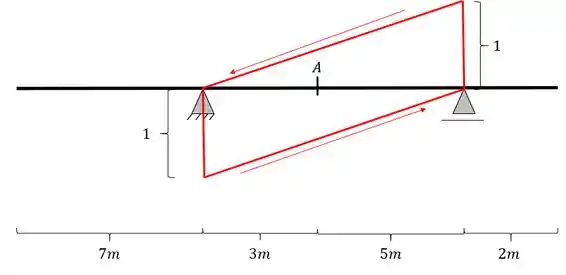
Passo 4
Para o próximo passo podemos ver que a nossa barra possui balanço em ambos os lados, e dessa forma, prolongando essa linha até o balanço, teremos que a nossa linha de influência ficará da seguinte maneira
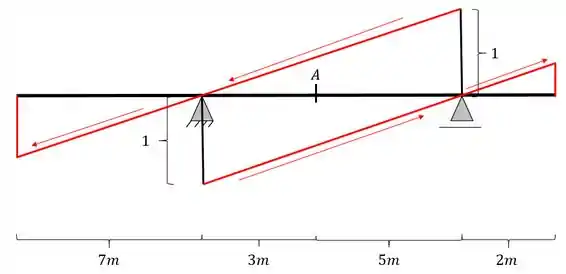
Passo 5
Agora iremos passar a nossa reta transversal, ligando as retas paralelas que passam nos apoios, passando pela nossa seção A que está sendo calculada, dessa forma teremos a seguinte estrutura
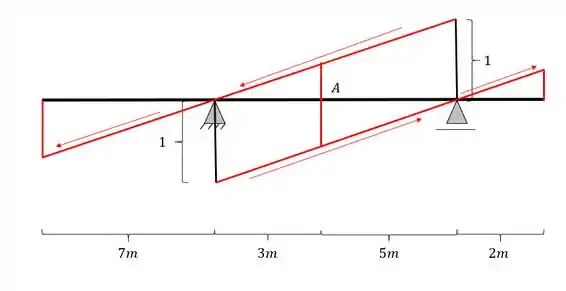
Passo 6
Agora já podemos fazer as 2 regras de 3 levando em consideração os seguintes triângulos
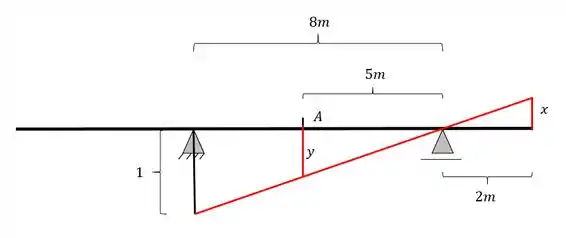
Teremos aqui a seguinte regra de 3, calculando primeiro x
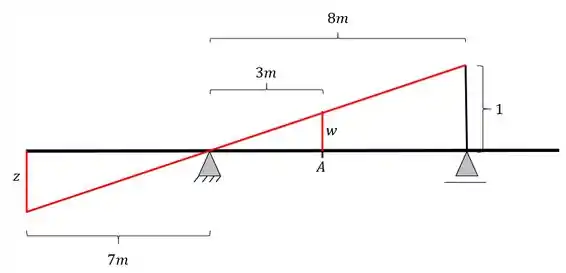
Calculando agora Y, teremos o seguinte
Calculando agora Z, teremos o seguinte
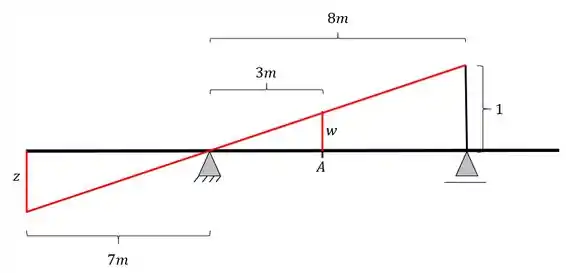
Calculando agora w, teremos o seguinte
E somando Y+W teremos exatamente o valor central que tem que dar 1 já que as nossas retas são paralelas
O que comprova que de fato fizemos tudo certo já que o valor central está mantido em 1.
Passo 7
Agora que já fizemos tudo basta apagarmos as nossas linhas de construção, e o que irá sobrar será exatamente a nossa linha de influência da viga
Apagando essas linhas e acrescentando os valores calculados na regra de 3 teremos a seguinte linha de influencia
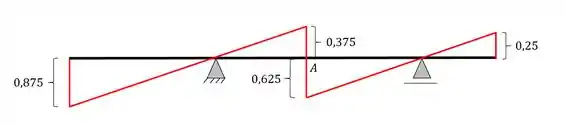
Resposta
Linha de Influência de cortantes na seção A por métodos gráficos.