Treliça Método das Seções - Método de Richter
Produzido por Pablo RicardoTeoria
Fala aí! Bora conversar sobre o Método das Secções de Richter?
Já vamos começar com tudo! Imagine que o seu professor pedisse a força normal que age nas barras
Socorro! 😱😱😱
Perceba que a barra
Para resolver esse tipo de problema, eu os apresento ao Método da Seção de Richter! Se liga nesse videozinho abaixo com tudo o que você precisa saber para usar esse método! 👇
Ou continua comigo no textinho 👇
Método das Seções
O método das seções consiste em cortar a treliça em seções escolhidas de forma estratégica. Devemos tomar os seguintes cuidados nessa escolha!
-Como assim?
Vou te explicar!
O método é mais simples quando cortamos até
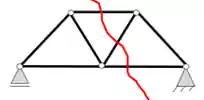
Se cortarmos mais de
Nesse exemplo a linha vermelha representa a nossa seção, veja que ela corta apenas
Passo a Passo do Método de Richter
Bora aprender esse passo a passo com exemplo?!
Passo 1: Reações de Apoio
Usando as fórmulas de equilíbrio teremos que:
Considerando as barras horizontais com tamanhos iguais e as barras verticais também com tamanhos iguais entre elas teremos que:
Logo o equilíbrio de momentos será:
Sabendo que
:
Como a reação em
Passo 2: Seção de Richter e a Escolha do Lado
Agora partimos para o nosso objetivo! Como desejamos saber o normal na barra
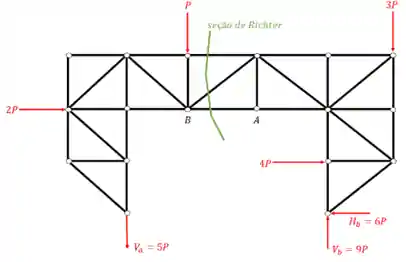
Perceba que conseguimos cortar só
Agora vem uma decisão mais arbitraria. Temos que escolher umas das duas seções para ficar e uma para ser descartada.
Vamos escolher a que parece mais fácil pra ficar!
A que parece mais simples é a da esquerda, pois possui menos forças para se preocupar do que o lado direito. Então manteremos a seção da esquerda! Vai ficar assim:
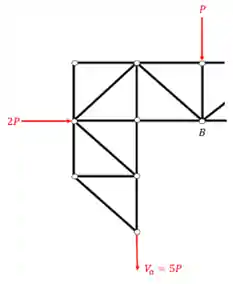
Passo 3: Equilíbrio da Seção
Queremos que a estrutura fique equilibrada, mas arrancamos metade dela, o que faremos? 😵💫
Devemos repor na estrutura o que lhe foi retirado, como em treliças apenas temos cargas nos nós, e a estrutura é toda rotulada, teremos apenas forças normais, ou seja, basta repormos as forças normais nas barras que cortamos e a partir daí fazermos o equilíbrio:
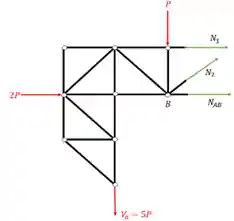
Perceba que arbitramos os normais saindo das barras pois se derem negativo, significará compressão e se derem positivo tração.
Agora já temos tudo, uma estrutura equilibrada, com as reações de apoio calculada, com os normais de incógnitas, maaaaaas, você percebeu que temos três incógnitas e três equações, certo? Mas lembra que eu perturbei para arrumarmos uma seção em que duas das barras fossem para um mesmo nó? Você sabe o porquê disso?
O motivo é bem simples, se você fizer o somatório de momentos nesse nó para o qual as duas barras apontam, você tira duas incógnitas da equação com uma cajadada só, e olha que genial, a única incógnita que sobra é exatamente a que você precisa.
Passo 4: Cálculo da Normal
Olhando a nossa peça temos:
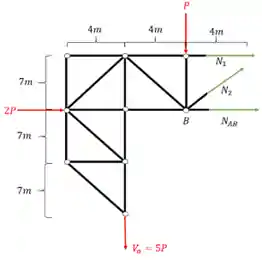
Fazendo o somatório de momento no nó que
Com isso temos:
E calculamos dessa forma o nossa normal!
Confere esse exercício resolvido em vídeo, sobre
Vamos praticar com mais exercícios?
Método das Seções
Passo a Passo do Método de Richter
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine o valor do normal na barra BC da treliça, usando o método da seção de Richter.
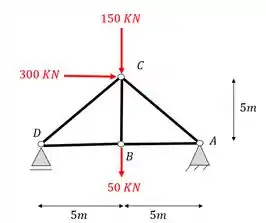
Passo 1
Para resolvermos a nossa treliça pelo método da seção de Richter precisamos ter em mente o seguinte passo a passo.
- Primeiro devemos calcular as reações de apoios da nossa treliça, que será calculada levando em consideração dois fatores
- A segunda coisa que temos que fazer é passar uma seção que corte a barra que pretendemos calcular, e que além disso respeite a regrinha de cortar apenas 3 barras.
- A terceira coisa que devemos fazer é eliminar um dos lados da treliça quando tivermos definido a seção de Richter.
- A quarta coisa que devemos fazer é o equilíbrio da seção que nos restar. Nesse equilíbrio iremos calcular os normais das barras que tivermos cortado.
- Por fim, o quinto e último passo consiste em escolher a melhor forma de fazer o equilíbrio das seções. Na grande maioria das vezes a melhor atitude a se tomar é calcular o somatório de momentos em um nó que receba duas barras da nossa seção cortada, pois pense bem, se cortamos 3 barras e vamos fazer o somatório de momentos em um nó que recebe 2 barras, no nosso problema teremos apenas 1 incógnita, e assim essa incógnita será exatamente o normal de um das barras.
As reações

E as equações de equilíbrio
Entendido o nosso passo a passo, vamos usá-lo no nosso exercício.
Passo 2
A primeira coisa que devemos fazer como vimos no nosso passo a passo é definir as reações de apoio. Para isso devemos primeiro determinar os vetores reações de apoio e lembrar que sempre consideramos a nossa treliça como um elemento solido e único que usamos para determinar essas reações, com isso teremos que o nosso diagrama de corpo livre será
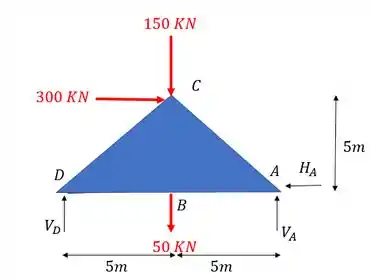
Definido os vetores reações de apoio já podemos usar as fórmulas de equilíbrio
Substituindo
Como tivemos uma reação de apoio negativa, podemos inverter o vetor para usarmos esse carregamento positivo, fazendo isso teremos
Assim já cumprimos a primeira parte do nosso passo a passo.
Passo 3
A segunda parte do problema consiste em cortar as barras que queremos calcular os normais, lembrando de respeitar a regra das 3 barras. Se der para cortar todas que queremos calcular de uma só vez, podemos fazer isso, se não, vale apena fazer uma de cada vez, caso não seja possível cortar tudo com uma única seção de Richter. No nosso exercício conseguimos fazer isso, conseguimos cortar 3 barras, com uma seção, e uma dessas barras é exatamente a que queremos determinar.
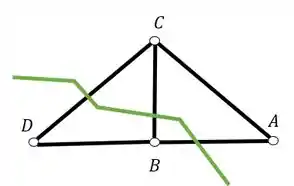
Passo 4
O quarto passo consiste em escolher um dos lados da seção para permanecer e descartar o outro lado da seção. Se pararmos para olhar a nossa seção com os carregamentos
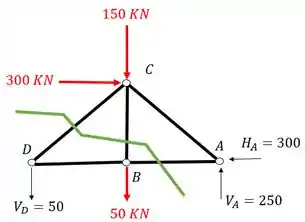
Podemos ver que a parte da treliça a direita da seção de Richter vermelha possui mais carregamentos do que do lado esquerdo, logo, para ficar mais fácil de calcular, iremos descartar o direito, e permaneceremos com o lado esquerdo.
Passo 5
Primeiro separamos a seção que iremos calcular
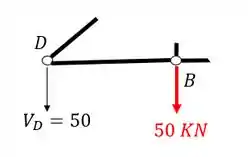
E sabemos que devemos, para toda barra cortada, colocar um normal saindo da seção que foi cortada, o que simboliza exatamente o quarto passo do nosso passo a passo.
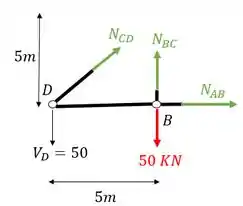
Passo 6
Agora o quinto e último passo consiste em escolhermos a melhor opção para fazermos o equilíbrio dos normais.
Veja que por exemplo, se quisermos calcular o normal BC, precisamos fazer o equilíbrio de momentos fletores no nó D, sabemos o seu posicionamento, e por isso podemos fazer o somatório de momentos nele.
Mas você pode se perguntar, porque o nó D?
Veja que as barras CD e AB se encontram no ponto D, e além disso, são incógnitas, ou seja, se fizermos o somatória de momentos no nó D, que sabemos que tem que ser igual a zero por ser uma treliça, teremos que a única incógnita do problema será que queremos calcular, fazendo isso teremos
Substituindo
Viu como é simples? Com 3 linhas já achamos o valor do normal .
Resposta
Exercício Resolvido #2
Elaboração Própria
Determine o normal da barra AB e CD da treliça abaixo, usando o método da seção de Richter.
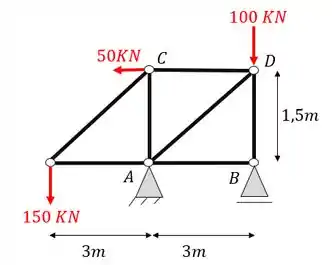
Passo 1
Para resolvermos a nossa treliça pelo método da seção de Richter precisamos ter me mente o seguinte passo a passo.
- Primeiro devemos calcular as reações de apoios da nossa treliça, que será calculada levando em consideração dois fatores
- A segunda coisa que temos que fazer é passar uma seção que corte a barra que pretendemos calcular, e que além disso respeite a regrinha de cortar apenas 3 barras.
- A terceira coisa que devemos fazer é eliminar um dos lados da treliça quando tivermos definido a seção de Richter.
- A quarta coisa que devemos fazer é o equilíbrio da seção que nos restar. Nesse equilíbrio iremos calcular os normais das barras que tivermos cortado.
- Por fim, o quinto e último passo consiste em escolher a melhor forma de fazer o equilíbrio das seções. Na grande maioria das vezes a melhor atitude a se tomar é calcular o somatório de momentos em um nó que receba duas barras da nossa seção cortada, pois pense bem, se cortamos 3 barras e vamos fazer o somatório de momentos em um nó que recebe 2 barras, no nosso problema teremos apenas 1 incógnita, e assim essa incógnita será exatamente o normal de um das barras.
As reações

E as equações de equilíbrio
Entendido o nosso passo a passo, vamos usá-lo no nosso exercício.
Passo 2
A primeira coisa que devemos fazer como vimos no nosso passo a passo é definir as reações de apoio. Para isso devemos primeiro determinar os vetores reações de apoio e lembrar que sempre consideramos a nossa treliça como um elemento solido e único que usamos para determinar essas reações, com isso teremos que o nosso diagrama de corpo livre será
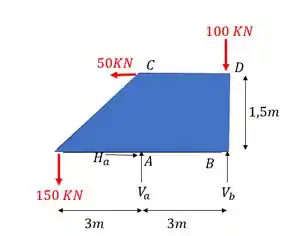
Definido os vetores reações de apoio já podemos usar as fórmulas de equilíbrio
Substituindo
Como deu negativo, sabemos que só significa que a direção do vetor que escolhemos está equivocada, ou seja, basta mudarmos a direção do vetor para ficarmos com a direção correta e assim podermos usar o sinal positivo ao invés do negativo
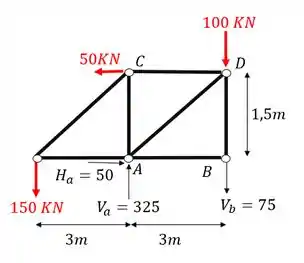
Assim já cumprimos a primeira parte do nosso passo a passo.
Passo 3
A segunda parte do problema consiste em cortar as barras que queremos calcular os normais, lembrando de respeitar a regra das 3 barras. Se der para cortar todas que queremos calcular de uma só vez, podemos fazer isso, se não, vale apena fazer uma de cada vez, caso não seja possível cortar tudo com uma única seção de Richter. No nosso exercício, conseguimos fazer isso, cortar 3 barras, e das 3 que cortamos, duas são as que precisamos calcular, em baixo temos a nossa seção
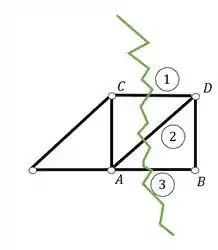
Passo 4
O quarto passo consiste em escolher um dos lados da seção para permanecer e descartar o outro lado da seção. Se pararmos para olhar a nossa seção com os carregamentos
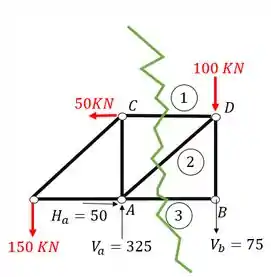
Podemos ver que a parte da treliça a esquerda da seção de Richter possui muito mais carregamentos do que a seção do lado direito, logo, para ficar mais fácil de calcular, iremos descartar o lado esquerdo, e permaneceremos com o lado direito, com isso a nossa seção passa a ser
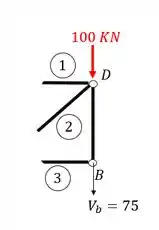
E sabemos que devemos, para toda barra cortada, colocar um normal saindo da seção que foi cortada, o que simboliza exatamente o quarto passo do nosso passo a passo.
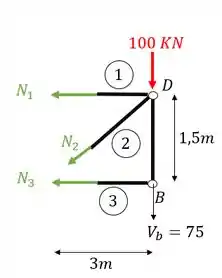
Passo 5
Agora o quinto e último passo consiste em escolhermos a melhor opção para fazermos o equilíbrio dos normais.
Veja que por exemplo, se quisermos calcular o normal 1, precisamos fazer o equilíbrio de momentos fletores no nó A, que mesmo sendo descartado por estar na parte esquerda da treliça, sabemos o seu posicionamento, e por isso podemos fazer o somatório de momentos nele.
Mas você pode se perguntar, porque o nó A?
Veja que as barras AD e AB se encontram no ponto A, e além disso, são incógnitas, ou seja, se fizermos o somatória de momentos no nó A, que sabemos que tem que ser igual a zero por ser um treliça, teremos que a única incógnita do problema será que queremos calcular, fazendo isso teremos
Viu como é simples? Com 3 linhas já achamos o valor do normal .
Porém também é pedido no enunciado o normal da barra 3, ou seja, , vamos lá então.
Passo 6
Agora qual seria a melhor opção para calcularmos o ?
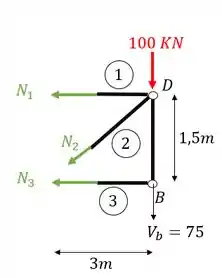
Vemos que nesse caso a melhor opção seria fazer o somatório de momentos no nó D, pois veja que as barras 1 e 2 são incógnitas (fingindo que anda não temos o normal 1), e ambas as barras chegam no nó D, ou seja, quando fizermos essa conta a única incógnita que restará será o , vamos lá então.
Ou seja, mais 3 linhas calculamos o segundo normal, e veja que a barra 1 representa a barra CD, e a barra 3 representa a barra AB, que são as pedidas no enunciado, dessa forma podemos escrever os normais como.
Resposta
Exercício Resolvido #3
Elaboração Própria
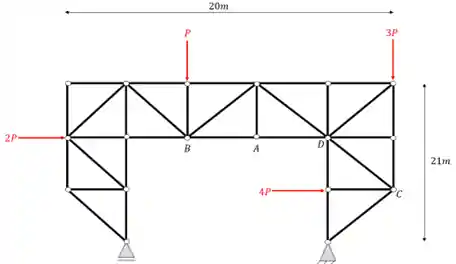
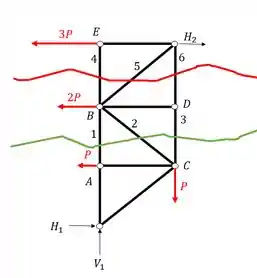
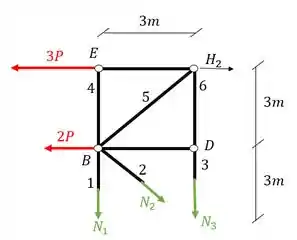
Determine o valor dos normais em função de P das barras AB, CD e BE da treliça dada abaixo usando o método da seção de Richter.
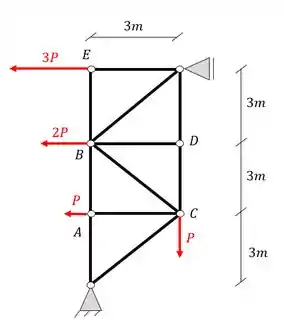
Passo 1
Para resolvermos a nossa treliça pelo método da seção de Richter precisamos ter me mente o seguinte passo a passo.
- Primeiro devemos calcular as reações de apoios da nossa treliça, que será calculada levando em consideração dois fatores
- A segunda coisa que temos que fazer é passar uma seção que corte a barra que pretendemos calcular, e que além disso respeite a regrinha de cortar apenas 3 barras.
- A terceira coisa que devemos fazer é eliminar um dos lados da treliça quando tivermos definido a seção de Richter.
- A quarta coisa que devemos fazer é o equilíbrio da seção que nos restar. Nesse equilíbrio iremos calcular os normais das barras que tivermos cortado.
- Por fim, o quinto e último passo consiste em escolher a melhor forma de fazer o equilíbrio das seções. Na grande maioria das vezes a melhor atitude a se tomar é calcular o somatório de momentos em um nó que receba duas barras da nossa seção cortada, pois pense bem, se cortamos 3 barras e vamos fazer o somatório de momentos em um nó que recebe 2 barras, no nosso problema teremos apenas 1 incógnita, e assim essa incógnita será exatamente o normal de um das barras.
As reações

E as equações de equilíbrio
Entendido o nosso passo a passo, vamos usá-lo no nosso exercício.
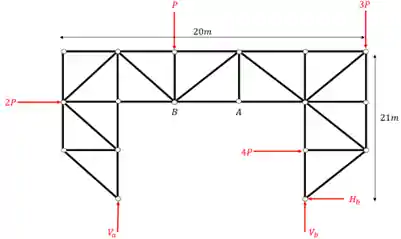
Passo 2
A primeira coisa que devemos fazer como vimos no nosso passo a passo é definir as reações de apoio. Para isso devemos primeiro determinar os vetores reações de apoio e lembrar que sempre consideramos a nossa treliça como um elemento solido e único que usamos para determinar essas reações, com isso teremos que o nosso diagrama de corpo livre será
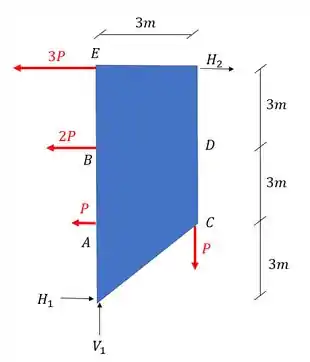
Definido os vetores reações de apoio já podemos usar as fórmulas de equilíbrio
Substituindo
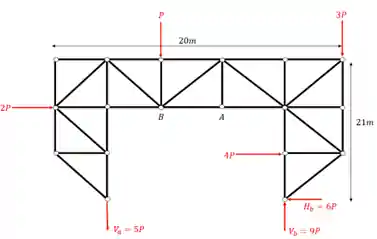
Assim já cumprimos a primeira parte do nosso passo a passo.
Passo 3
A segunda parte do problema consiste em cortar as barras que queremos calcular os normais, lembrando de respeitar a regra das 3 barras. Se der para cortar todas que queremos calcular de uma só vez, podemos fazer isso, se não, vale apena fazer uma de cada vez, caso não seja possível cortar tudo com uma única seção de Richter. No nosso exercício não conseguimos fazer isso, conseguimos cortar 2 barras, com uma seção, e a outra teremos que usar outra seção. Na figura abaixo desenhamos as duas seções, mas faremos uma de cada vez.
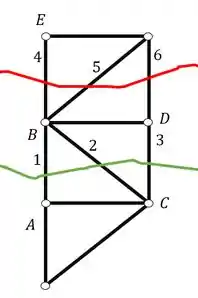
Passo 4
O quarto passo consiste em escolher um dos lados da seção para permanecer e descartar o outro lado da seção. Se pararmos para olhar a nossa seção com os carregamentos
Podemos ver que a parte da treliça abaixo da seção de Richter possui mais carregamentos do que a seção do lado de cima, logo, para ficar mais fácil de calcular, iremos descartar o lado de baixo, e permaneceremos com o lado de cima, e perceba que para ambas as seções (verde e vermelha) a parte de cima é mais fácil de calcular.
Vamos então fazer o primeiro calculo para a seção verde.
Passo 5
Primeiro separamos a seção que iremos calcular
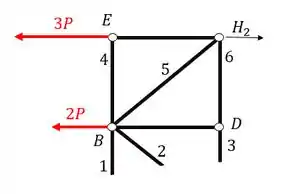
E sabemos que devemos, para toda barra cortada, colocar um normal saindo da seção que foi cortada, o que simboliza exatamente o quarto passo do nosso passo a passo.
Passo 6
Agora o quinto e último passo consiste em escolhermos a melhor opção para fazermos o equilíbrio dos normais.
Veja que por exemplo, se quisermos calcular o normal 1, precisamos fazer o equilíbrio de momentos fletores no nó C, que mesmo sendo descartado por estar na parte de baixo da treliça, sabemos o seu posicionamento, e por isso podemos fazer o somatório de momentos nele.
Mas você pode se perguntar, porque o nó C?
Veja que as barras BC e DC se encontram no ponto C, e além disso, são incógnitas, ou seja, se fizermos o somatória de momentos no nó C, que sabemos que tem que ser igual a zero por ser uma treliça, teremos que a única incógnita do problema será que queremos calcular, fazendo isso teremos
Substituindo
Viu como é simples? Com 3 linhas já achamos o valor do normal .
Porém também é pedido no enunciado o normal da barra 3, ou seja, , vamos lá então.
Passo 7
Agora qual seria a melhor opção para calcularmos o ?
Vemos que nesse caso a melhor opção seria fazer o somatório de momentos no nó B, pois veja que as barras 1 e 2 são incógnitas (fingindo que ainda não temos o normal 1), e ambas as barras chegam no nó B, ou seja, quando fizermos essa conta a única incógnita que restará será o , vamos lá então.
substituindo
Ou seja, mais 3 linhas calculamos o segundo normal, e veja que a barra 1 representa a barra AB, e a barra 3 representa a barra CD, que são as pedidas no enunciado, dessa forma podemos escrever os normais como.
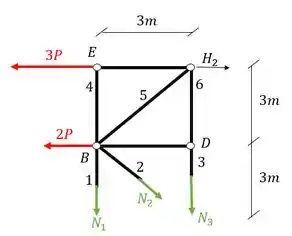
Vamos agora fazer a segunda seção de Richter que é a vermelha.
Passo 8
Primeiro separamos a seção que iremos calcular
E sabemos que devemos, para toda barra cortada, colocar um normal saindo da seção que foi cortada, o que simboliza exatamente o quarto passo do nosso passo a passo.
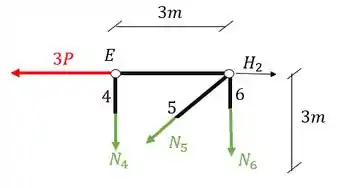
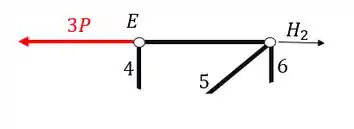
Passo 9
Agora o quinto e último passo consiste em escolhermos a melhor opção para fazermos o equilíbrio dos normais.
Veja que por exemplo, se quisermos calcular o normal 4, precisamos fazer o equilíbrio de momentos fletores no nó F, que tem a reação , sabemos o seu posicionamento, e por isso podemos fazer o somatório de momentos nele.
Mas você pode se perguntar, porque o nó F?
Veja que as barras BF e DF se encontram no ponto F, e além disso, são incógnitas, ou seja, se fizermos o somatória de momentos no nó F, que sabemos que tem que ser igual a zero por ser uma treliça, teremos que a única incógnita do problema será que queremos calcular, fazendo isso teremos
Substituindo
Viu como é simples? Com 3 linhas já achamos o valor do normal .
Veja que a barra 4 representa a barra BE, que é pedida no enunciado, dessa forma podemos escrever o normal como.
Resposta
Exercício Resolvido #4
Elaboração Própria
Dada a treliça abaixo, determine o valor do normal nas barras AB e CD usando o método da seção de Richter.
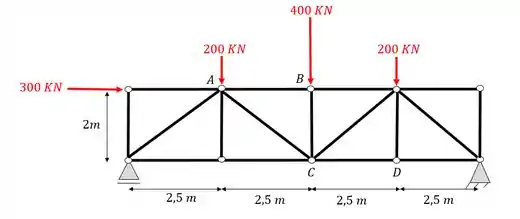
Passo 1
Para resolvermos a nossa treliça pelo método da seção de Richter precisamos ter em mente o seguinte passo a passo.
- Primeiro devemos calcular as reações de apoios da nossa treliça, que será calculada levando em consideração dois fatores
- A segunda coisa que temos que fazer é passar uma seção que corte a barra que pretendemos calcular, e que além disso respeite a regrinha de cortar apenas 3 barras.
- A terceira coisa que devemos fazer é eliminar um dos lados da treliça quando tivermos definido a seção de Richter.
- A quarta coisa que devemos fazer é o equilíbrio da seção que nos restar. Nesse equilíbrio iremos calcular os normais das barras que tivermos cortado.
- Por fim, o quinto e último passo consiste em escolher a melhor forma de fazer o equilíbrio das seções. Na grande maioria das vezes a melhor atitude a se tomar é calcular o somatório de momentos em um nó que receba duas barras da nossa seção cortada, pois pense bem, se cortamos 3 barras e vamos fazer o somatório de momentos em um nó que recebe 2 barras, no nosso problema teremos apenas 1 incógnita, e assim essa incógnita será exatamente o normal de um das barras.
As reações

E as equações de equilíbrio
Entendido o nosso passo a passo, vamos usá-lo no nosso exercício.
Passo 2
A primeira coisa que devemos fazer como vimos no nosso passo a passo é definir as reações de apoio. Para isso devemos primeiro determinar os vetores reações de apoio e lembrar que sempre consideramos a nossa treliça como um elemento solido e único que usamos para determinar essas reações, com isso teremos que o nosso diagrama de corpo livre será
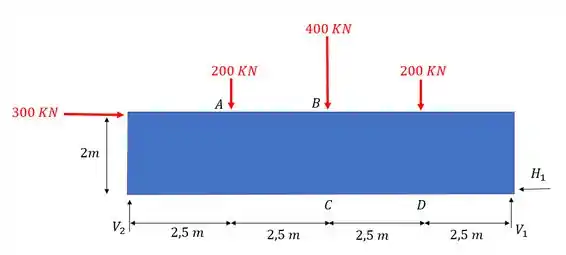
Definido os vetores reações de apoio já podemos usar as fórmulas de equilíbrio
Substituindo
Assim já cumprimos a primeira parte do nosso passo a passo.
Passo 3
A segunda parte do problema consiste em cortar as barras que queremos calcular os normais, lembrando de respeitar a regra das 3 barras. Se der para cortar todas que queremos calcular de uma só vez, podemos fazer isso, se não, vale apena fazer uma de cada vez, caso não seja possível cortar tudo com uma única seção de Richter. No nosso exercício não conseguimos fazer isso, conseguimos cortar 1 barra, com uma seção, e a outra teremos que usar outra seção. Na figura abaixo desenhamos as duas seções, mas faremos uma de cada vez.
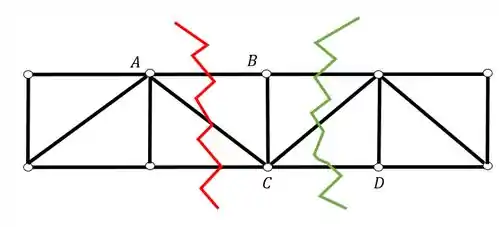
Passo 4
O quarto passo consiste em escolher um dos lados da seção para permanecer e descartar o outro lado da seção. Se pararmos para olhar a nossa seção com os carregamentos
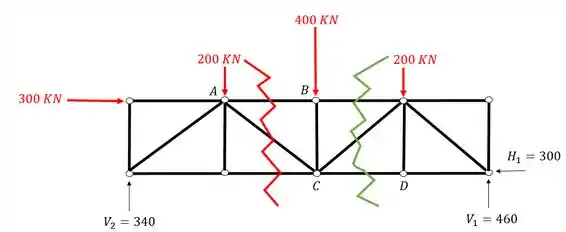
Podemos ver que a parte da treliça a direita da seção de Richter vermelha possui mais carregamentos do que do lado esquerdo, logo, para ficar mais fácil de calcular, iremos descartar o direito, e permaneceremos com o lado esquerdo.
Vamos então fazer o primeiro cálculo para a seção vermelha.
Passo 5
Primeiro separamos a seção que iremos calcular
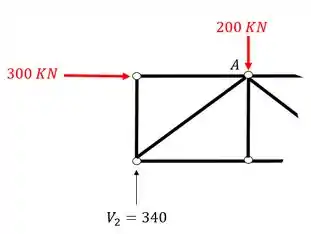
E sabemos que devemos, para toda barra cortada, colocar um normal saindo da seção que foi cortada, o que simboliza exatamente o quarto passo do nosso passo a passo.
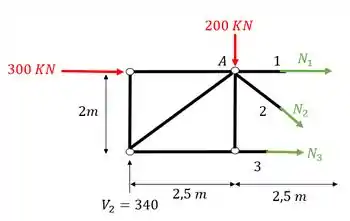
Passo 6
Agora o quinto e último passo consiste em escolhermos a melhor opção para fazermos o equilíbrio dos normais.
Veja que por exemplo, se quisermos calcular o normal 1, precisamos fazer o equilíbrio de momentos fletores no nó C, que mesmo sendo descartado por estar na parte de baixo da treliça, sabemos o seu posicionamento, e por isso podemos fazer o somatório de momentos nele.
Mas você pode se perguntar, porque o nó C?
Veja que as barras 2 e 3 se encontram no ponto C, e além disso, são incógnitas, ou seja, se fizermos o somatória de momentos no nó C, que sabemos que tem que ser igual a zero por ser uma treliça, teremos que a única incógnita do problema será que queremos calcular, fazendo isso teremos
Substituindo
Viu como é simples? Com 3 linhas já achamos o valor do normal .
Porém também é pedido no enunciado o normal da barra CD, que será calculada com a seção verde, vamos para a próxima seção de Richter.
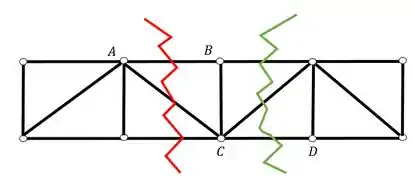
Podemos ver que a parte da treliça a esquerda da seção de Richter verde possui mais carregamentos do que do lado direito, logo, para ficar mais fácil de calcular, iremos descartar a esquerda, e permaneceremos com o lado direito.
Vamos então fazer o cálculo da seção verde.
Passo 7
Primeiro separamos a seção que iremos calcular
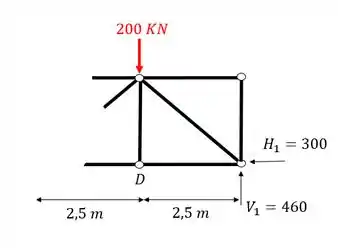
E sabemos que devemos, para toda barra cortada, colocar um normal saindo da seção que foi cortada, o que simboliza exatamente o quarto passo do nosso passo a passo.
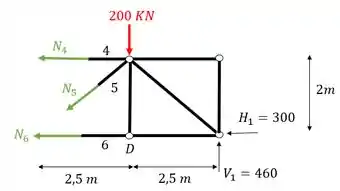
Passo 8
Agora o quinto e último passo consiste em escolhermos a melhor opção para fazermos o equilíbrio dos normais.
Veja que por exemplo, se quisermos calcular o normal 6, precisamos fazer o equilíbrio de momentos fletores no nó com a carga de 200KN, sabemos o seu posicionamento, e por isso podemos fazer o somatório de momentos nele.
Mas você pode se perguntar, porque o nó com a carga de 200KN?
Veja que as barras 4 e 5 se encontram nesse nó, e além disso, são incógnitas, ou seja, se fizermos o somatória de momentos nesse nó, que sabemos que tem que ser igual a zero por ser uma treliça, teremos que a única incógnita do problema será que queremos calcular, fazendo isso teremos
Substituindo
Viu como é simples? Com 3 linhas já achamos o valor do normal .
E veja que as barras 1 e 6 são as barras que precisávamos calcular, logo, podemos reescrever esses normais como