Para o pêndulo mostrado na Figura que modela um tipo de sismógrafo: determinar a frequência natural.
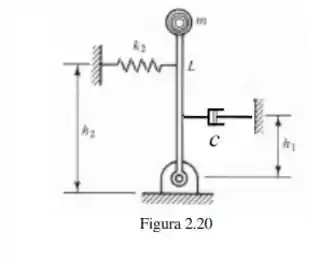
Passo 1
Primeiro vamos começar o problema, entendendo o que estamos buscando e como vamos chegar à solução. Ok?
Pois bem, estamos buscando a frequência natural do sistema harmônico com amortecimento . De acordo com a Teoria, se chegarmos a uma modelagem envolvendo uma EDO de 2º ordem como essa genérica aqui:
Então a frequência natural pode ser encontrada a partir do termo que multiplica . Então, no problema, basicamente devemos modelar o nosso problema e ver se a gente encontra algo parecido. Vamos nessa?
Passo 2
Para a modelagem, vamos começar partindo do modelo físico que rege o nosso sismógrafo: as Leis de Newton para pêndulos!
Em pêndulos, estamos interessados em saber qual é o ângulo a seguir com o tempo :
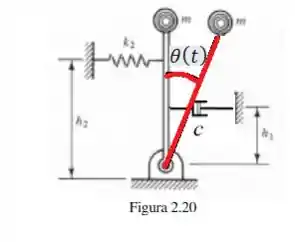
Basicamente, no problema temos três forças criando torques nesse pêndulo, o fazendo balançar com esse :
- Torque da força peso da bolinha .
- Torque da força elástica da molinha .
- E por último, Torque da força de amortecimento .
De acordo com Newton, a soma desses torques é um torque resultante e que é diferente , já que o pêndulo não está estático:
Vamos falar nos próximos passos, o que são cada torque representa. Vamos lá!
Passo 3
Primeiro vamos falar do torque resultante .
Toda vez que temos um pêndulo girando, então podemos calcular o torque resultante dessa forma aqui:
Onde é à distância da força ao ponto de rotação, enquanto é a força perpendicular ao movimento. Pelo diagrama a seguir, podemos ver quem é essa força:
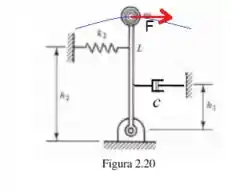
O movimento é sempre dado pela trajetória em azul. Como a trajetória em azul é um arco, então, podemos encontrar tal arco de acordo com a equação:
Ou seja, é o produto do raio pelo arco !
Sabemos que onde a aceleração é a derivada segunda da trajetória: :
Portanto, o Torque resultante será:
Passo 4
Vamos agora falar do torque causado pela força peso da bolinha:
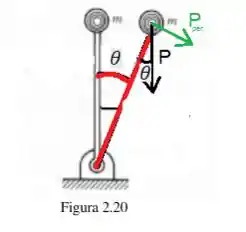
Veja que a única força que de fato importa não é nem o Peso em si, e sim a componente dela perpendicular ao movimento . Essa força pode ser obtida da seguinte forma:
Onde ...
Portanto, o torque causado por essa força peso será:
Como o ângulo é pequeno, podemos eliminar esse seno com uma ótima simplificação:
Logo, podemos dizer que...
Passo 5
Não desista, pois estamos indo bem, faltam ainda dois torques para analisarmos e vamos começar aqui com o :
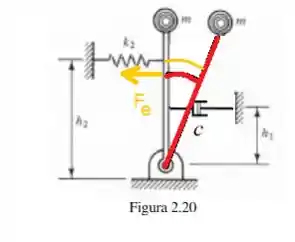
O torque dessa força elástica é dado por:
Onde é a distância de aplicação da força ao ponto de rotação. Enquanto que a força elástica é dada por:
Onde é a trajetória em laranja. De forma análoga ao cálculo da trajetória em azul no passo 3...
Ou seja, é o produto do raio, que agora é pelo arco...
Logo...
Passo 6
Beleza, agora vamos para o último torque que é o da força de amortecimento ...
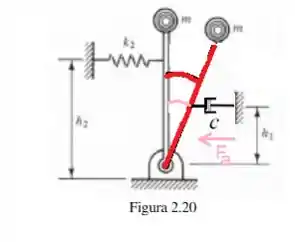
Agora, por definição de torque...
Onde é a força de amortecimento proporcional a velocidade...
A velocidade , entretanto, é a derivada primeira da trajetória circular em rosa dada por (assim como calculamos qualquer trajetória circular anteriormente é o produto do raio pelo arco )...
Logo...
Passo 7
Finalmente, depois de todos os torques calculados, podemos retornar para a igualdade do nosso querido passo onde deixamos o problema...
Substituindo todos os passos anteriores...
Passando tudo para um lado só...
Reorganizando...
Para comparar com essa EDO aqui
E descobrirmos quem é o , podemos dividir todos os termos por ...
Prontinho! De fato a equação que modela o nosso problema é uma EDO de 2º ordem, e podemos concluir que a frequência angular é...