Agitação e Mistura II
Produzido por Marcelo AlvesTeoria
Dimensões de um tanque agitado
Antes de continuarmos estudando agitação, precisamos combinar uma forma de chamar as dimensões de um tanque agitado, porque vamos precisar disso pra fazer cálculos.
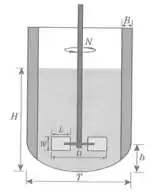
Em que:
- : altura do líquido
- : diâmetro do tanque
- : diâmetro do impelidor
- : altura da pá do impelidor
- : largura da pá do impelidor
- : distância entre o impelidor e o fundo do tanque
- : largura da chicana
- : número de rotações do impelidor
Número de potência
A gente pode escrever um balanço de energia pro fluido sendo agitado. Vamos adotar dois pontos pra fazer o balanço: inicial (1) e final (2).
Em que:
- é a perda de carga no trajeto
- é o trabalho adicionado devido à ação do impelidor
O lance é que o movimento dentro do tanque é circular; se olharmos pra uma partícula de fluido, ele sai de um ponto e acaba voltando pro mesmo ponto. Então e:
Simplificando a equação, podemos escrever:
E podemos escrever a perda de carga em função da velocidade do fluido e de uma constante .
E podemos, também, a partir disso, obter uma expressão para potência útil, que é a potência efetivamente transferida ao fluido. Sabendo que a velocidade é proporcional a , chegamos em:
Em que:
A definição do número de potência é:
- “Mas o que o me diz ?!”
Repara que na definição do entra o , que é uma medida do atrito. Isso deve te ajudar a lembrar que o número de potência é uma medida do efeito do atrito devido ao grau de agitação sendo feita e das características geométricas do tanque agitado.
- “OK. Entendi o que é o , mas como calculo?”
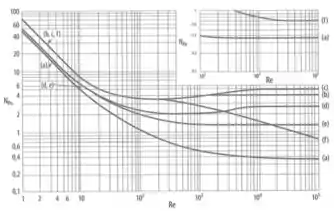
Lembra do diagrama de Moody lá de Mecânica dos fluidos? Nele, nos achávamos o coeficiente de atrito de Moody a partir do número de Reynolds. Caso não esteja lembrando pelo nome, olha ele aqui:

Estou falando dele porque pra achar o é muito parecido, também é função do número de Reynolds, só que agora em relação ao impelidor. A definição dele é:
Outro ponto que muda é que, no diagrama de Moody, as curvas eram diferentes em função de ; já pro , elas se diferenciam em função de diferentes tipos de impelidor. Bora dar uma olhada nele logo:
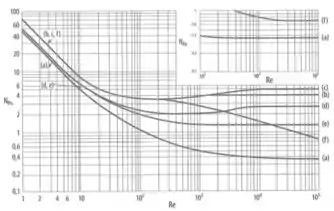
Em que:
- Hélice naval
- Pás retas
- Pás retas e disco (turbina de Rushton), com
- Pás encurvadas,
- Pás inclinadas com passo de e
- Pás retas sem chicana
Repara que todas as curvas têm 3 partes:
Nessa parte, podemos escrever:
Em que é uma constante relativa ao regime laminar (por isso o subscrito )
Nessa parte, é constante e podemos escrever:
Em que é uma constante relativa ao regime turbulento (por isso o subscrito )
Nível de agitação
Outra medida importante em se tratando de agitação é o nível de agitação , que é definido como uma relação entra a potência útil e o volume de líquido a ser agitado .
Quanto maior o , mais intensa é a agitação.
Número de Mistura
Agora pensa em um tanque agitado; vamos imaginar que ele tem uma entrada e uma saída. Concorda que quanto mais líquido eu jogo lá dentro mais líquido terei que agitar? E quanto mais tempo esse líquido passa lá dentro, maior é a quantidade de líquido pra agitar. Daí:
Isto é, o volume de líquido a ser agitado é proporcional a:
- : tempo de mistura
- : vazão volumétrica bombeada ao tanque
Calculamos o necessário baseado no número de mistura , cuja definição é:
Lembrando que é o número de rotações do impelidor.
O número de mistura também depende das características geométricas do tanque agitado (principalmente do impelidor) e do número de Reynolds. E sim, também tem gráfico pra achar o valor dele haha

Número de bombeamento
Sim, tem vários números em agitação. Mas relaxa que tá tudo conectado.
O número de bombeamento está relacionado com a vazão volumétrica. Esta é proporcional à velocidade de alimentação de fluido e à área do impelidor. E podemos escrever isso em termos de número de rotações do impelidor e do diâmetro dele:
Pra transformar isso em igualdade, a gente usa o número de bombeamento :
Aposto que você já até sabe o que eu vou dizer agora: também depende das características geométricas do tanque agitado e do número de Reynolds. E também tem gráfico pra achar o valor dele haha. Mas como os gráficos pra ele são mais limitados, não vou nem falar deles, ok?
Nível de agitação em função dos outros números
Pra visualizarmos a influência dos diversos números no nível de agitação, a gente pode ir substituindo as definições deles e chega em:
Correções no projeto de sistemas de agitação
E se o meu sistema de agitação precisar de mais de um impelidor? E se eu usar um impelidor diferente dos que todo mundo usa? E se além da agitação eu borbulhar um gás no tanque? Pra todos esses casos, vamos ter que modificar um pouco a forma de fazer os nossos cálculos, certo? Bora ver cada um deles:
- Se ao invés de um impelidor eu usar impelidores, a potência útil total dada ao sistema será:
- Até agora vimos estávamos assumindo tanque de agitação e impelidores “padrão”, mas nem sempre vai ser assim. Antes de qualquer coisa, deixa eu te mostrar o que é o padrão:
Em que é a potência útil de um único impelidor. Além disso, pra essa equação ser válida, esses impelidores não podem estar muito próximos; têm que estar a uma distância tal que
- Número de chicanas: 4
- Para turbinas como impelidor: e
- Para pás como impelidor:
- Para hélices como impelidor:
E se não for padrão, o que vamos fazer é corrigir a potência útil fornecida ao sistema; para isso, usamos um fator de correção .
E a fórmula pra esse fator é:
- A densidade aparente da mistura diminui, isto é, é como se tivesse um líquido menos denso pra agitar. Isso vai facilitar a agitação e diminuir a potência necessária.
- O ar sendo borbulhado já ajuda na agitação, o que também contribui pra diminuir a potência necessária.
Ou seja, injetar gás no sistema diminui a potência necessária pra agitar. Pra saber em quanto é essa redução, podemos usar um (adivinhaaaaa haha) gráfico.
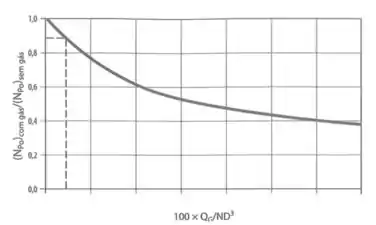
Em que é a vazão volumétrica de gás injetado no sistema.
Algo também é importante é que quando há borbulhamento de gás, é recomendável usar as seguintes relações geométricas:
- E as outras relações são iguais às apresentadas em b)
Nível de agitação N A
Número de Mistura N τ
Número de bombeamento N q
Nível de agitação N A em função dos outros números
Correções no projeto de sistemas de agitação
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Um tanque cilindrico é agitado por um impelidor que fornece
Devido a mudanças no processo, o nível de líquido será dobrado no tanque. Pede-se
- Visando manter o nível de agitação, qual deverá ser a nova potência de agitação?
- Quantos impelidores idênticos ao original serão necessários para fornecer tal potência?
Passo 1
Essa questão não chega a ser de mudança de escala porque não estamos mudando o tanque, apenas o nível de líquido no tanque.
Como o enunciado diz que o tanque é cilíndrico, podemos assumir seção transversal constante, daí ao dobrar o nível, isto é, altura de líquido, vamos estar dobrando a quantidade de líquido dentro do tanque.
Chamando o novo volume de líquido de e o original de , podemos afirmar que:
A primeira pergunta visa manter o nível de agitação constante. A definição do nível de agitação é:
Já a segunda pergunta é qual será o número de impelidores iguais ao original para fornecer a nova potência, que vou chamar de
Passo 2
- Visando manter o nível de agitação, qual deverá ser a nova potência de agitação?
Bora chamar o nível de agitação original de ; nome bem original haha De qualquer maneira, podemos escrevê-lo como:
Não sabemos o valor de então deixamos indicado.
Já o novo nível de agitação, vou chamar de , outro nome original haha Podemos escrevê-lo como:
E sabemos que
Substituindo isso:
E como queremos manter constante:
Substituindo as expressões que achamos pra esses dois:
Cortando os e isolando :
Passo 3
b)Quantos impelidores idênticos ao original serão necessários para fornecer tal potência?
Para resolver essa, temos que assumir que os que os impelidores estão suficientemente espaçados, daí, podemos usar
Em que é a potência total, é o número de impelidores e é a potência fornecida por um único dos n impelidores.
Substituindo os valore que temos:
Daí:
Resposta
Exercício Resolvido #2
Elaboração própria
Calcule o número de agitação para o caso de um tanque agitado de contendo de uma solução aquosa. Sabe-se que a potência útil do agitador vale
Passo 1
Esse problema é uma aplicação de fórmula direta, masssss calma pra não usar o dado errado.
Temos que calcular o número de agitação, cuja definição é:
Em que:
E
Repetindo: é o volume de líquido! NÃO é o volume do tanque; cuidado com isso, ok?
Fora isso, NÃO é adimensional, então não precisa se preocupar com unidades das coisas; pode usar a unidade que quiser, é só deixar indicado.
Passo 2
Bora pro cálculo. A definição do número de agitação é:
Temos que e . Daí:
Resposta
Exercício Resolvido #3
Cremaso, Marco Aurélio. Operações unitárias em sistemas particulados e fluidomecânicos, 2 ° e d - Adaptado
Considere a situação em que se deseja utilizar, para a homogeneização de um determinado biodiesel , um tanque de agitação que apresenta as seguintes características:
Estime o valor da potência consumida pelo sistema de agitação, assumindo que o tanque apresenta turbina de seis pás retas e:
- Quatro chicanas
- Sem chicanas
Passo 1
O enunciado já deu as dimensões do sistema de agitação e a quantidade de rotações do impelidor, . Daí para achar a potência, , usamos:
Como quase todos os dados fornecidos já estão no sistema de unidades CGS, é com ele que vou trabalhar. Por isso, vou converter essa rotação em rpm para o CGS, isto é, preciso de “por segundo” e não de “por minuto”:
Tanto no item a como no item b, os valores de (depende do fluido), (é dito constante) e (o tanque é o mesmo) se mantém iguais. Então posso substituir os valores e:
E como estamos trabalhando no CGS, isso está em .
Já o valor do depende do Reynolds e da configuração de cada tanque agitado. O Reynolds é calculado por:
Sendo que
O é dado como ; como a unidade padrão do CGS é St (Stokes):
Daí:
A partir do Reynolds, achamos o valor de pelo gráfico:
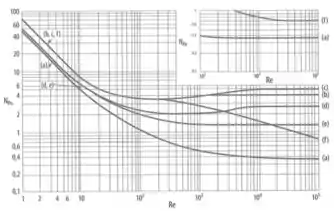
Como depende da configuração do tanque, vamos ter que ver isoladamente pra cada caso.
Passo 2
- Quatro chicanas
- Sem chicanas
O primeiro item pede a potência quando o tanque tem quatro chicanas (que é o “padrão”, como vimos na teoria. Como foi dito que o tanque apresenta pás retas, usamos a (b) do gráfico.
Olhando no gráfico a curva (b) para :
Daí:
Passo 3
Temos que fazer a mesma coisa do passo anterior, mas agora o tanque não tem chicanas então usamos a curva (f).
Olhando no gráfico a curva (f) para :
Daí:
Resposta
Exercício Resolvido #4
Cremaso, Marco Aurélio. Operações unitárias em sistemas particulados e fluidomecânicos, 2 ° e d
Deseja-se avaliar um sistema de agitação destinado à oxidação de matéria orgânica de um efluente que apresenta massa específica igual a e viscosidade dinâmica igual a . Conhecendo-se a capacidade de descarga do impelidor, que é igual a , e a vazão requerida de ar igual a , pede-se:
- Projete o sistema de agitação, utilizando um impelidor do tipo turbina de pás inclinadas de para um tanque de considerando-o em medidas padrão de modo que seu volume venha a ser maior do que o volume do líquido a ser agitado.
Passo 1
Algo que vamos precisar ter em mente nessa questão são as dimensões de um tanque agitado:
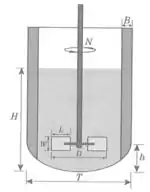
Em que:
- : altura do líquido
- : diâmetro do tanque
- : diâmetro do impelidor
- : altura da pá do impelidor
- : largura da pá do impelidor
- : distância entre o impelidor e o fundo do tanque
- : largura da chicana
- : número de rotações do impelidor
Podemos escrever o volume de líquido como:
Como há borbulhamento de gás, usamos:
Daí:
E foi dito que o volume do tanque é maior do que o volume de líquido:
E sabemos também que o volume do tanque é , que dá
Daí:
Passo 2
De
Conseguimos tirar que:
E, usando as outras relações geométricas, tiramos todas as outras dimensões. Vou organizar isso tudo melhor em uma tabela:

Resposta

Exercício Resolvido #5
Cremaso, Marco Aurélio. Operações unitárias em sistemas particulados e fluidomecânicos, 2 ° e d - Adaptado
Deseja-se avaliar um sistema de agitação destinado à oxidação de matéria orgânica de um efluente que apresenta massa específica igual a e viscosidade dinâmica igual a . Conhecendo-se a capacidade de descarga do impelidor, que é igual a , e a vazão requerida de ar igual a , pede-se:
b) Obtenha o valor da potência útil de agitação referente ao sistema projetado. Verifique também o nível de agitação.
Dados do tanque agitado:
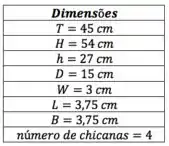
Passo 1
Para calcular a potência útil, vamos ter que usar:
Mas repara que NÃO temos o valor de e nem de :/ Bora procurar um jeito de resolver a questão então.
A gente tem a capacidade de descarga do impelidor:
E podemos escrever em função do número de bombeamento, :
Mas essa expressão também tem o , que não conhecemos...
Tem uma outra expressão que envolve o , que é o número de Reynolds do impelidor:
Embora a gente também não conheça o Reynolds (e nem tenha como determiná-lo de cara), a gente sabe que ele está relacionado tanto com o como com o . Os relacionamos pelos gráficos que vimos lá na teoria.
Para :
Para :
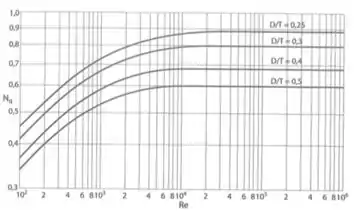
Sendo este gráfico apenas para impelidor do tipo turbinas de pás inclinadas a e com chicanas no tanque, que é o caso do problema.
O lance vai ser ficar iterando: chutar um valor de , calcular o Reynolds pra esse , daí calcular (pelo primeiro gráfico). Daí vamos “poder” calcular por:
Além disso, usamos esses mesmos e para achar um .
é dado como . O que vamos fazer é usar a equação:
E isolar o :
Nós vamos usar esse calculado para recalcular o . Daí usamos esse novo para repetir os cálculos. E vamos ficar repetindo isso até o valor de convergir, isto é, ficar constante. Aí teremos o valor de .
Passo 2
Antes de começar as iterações, vou já colocar o máximo de números possível no problema pra ficar com menos letras haha Começando com o Reynolds:
E aquela expressão do isolado:
Ah, outro detalhe é que vamos precisar de para obter o valor de do gráfico.
Repara que estou usando o CGS.
Vou organizar as iterações numa tabela. O primeiro chute vai ser .
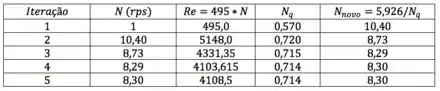
Um resumo dos resultados:
Passo 3
Agora que temos o Reynolds, podemos calcular o pra um sistema SEM borbulhamento pelo gráfico:
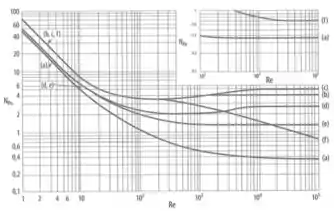
Usando o e a curva (e) (que vai ser uma aproximação já que não é exatamente ):
Ainda falta um detalhe: o nosso sistema é sim borbulhado então temos que corrigir o número de potência. Fazemos isso com aquele outro gráfico que vimos na teoria:
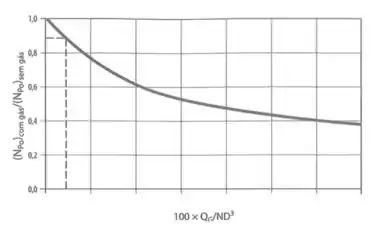
O valor no eixo x é:
Pelo gráfico:
Daí:
Passo 4
Finalmente podemos calcular o que a questão pede, :
Já o nível de agitação tem fórmula:
Não chegamos a calcular o , mas temos e sabemos que . Daí:
Usando em :