Teoria
Introdução
Fala, galera! Chegamos em um tópico bem importante e que vamos usar em todos os equipamentos de separação. Usamos um equipamento de separação para obter uma separação, né? Mas precisamos saber quão eficiente está sendo essa separação.
Bora ver o esquema de um equipamento de separação genérico:
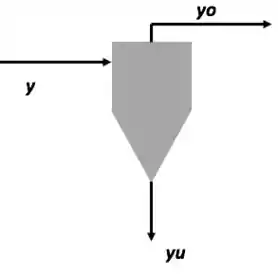
Apenas uma das correntes vai ser coletada e queremos saber quanto de partículas tem nessa corrente em relação ao que entrou no separador. Essa corrente mais rica em partículas vamos chamar de concentrado. Geralmente, ela vai ser a corrente que sai por baixo dos equipamentos e, por isso, vou usar "" (de underflow) como índice pra falar do concentrado. Isso de geralmente o concentrado sair por baixo é porque costumamos trabalhar com processos em que , ou seja, processos em que a densidade das partículas é maior que a do fluido.
Daí surge o nosso primeiro conceito:
Eficiência total (ou global) de separação
Já dei a dica na introdução:
E temos duas formas de calcular essa eficiência: nos baseando na massa de partículas () ou nos baseando no número de partículas (). A primeira é a que vamos usar quase sempre (ou sempre haha), mas bora ver os dois.
A eficiência calculada por massa fica:
Ou seja, a massa DE PARTÍCULAS que sai no concentrado dividido pela massa que entra.
Já a eficiência por número de partículas fica:
Em que é o número de partículas, é a concentração em número de partículas e é a vazão.
Agora, quero te mostrar outra relação que pode ser útil pra você.
Começamos pelo balanço de massa para partículas no separador:
Dividindo tudo por :
Isolando o e lembrando que :
Essa relação é útil pra quando precisarmos saber a concentração da corrente diluída e soubermos a eficiência. “Mas o importante é o concentrado!” Também, mas imagina que eu quero aumentar a recuperação de partículas e faço essa corrente do overflow ("") passar por um outro equipamento de separação. Daí ela vai ser importante.
Razão de fluido ()
A razão de fluido é quanto de FLUIDO sai no concentrado, junto com as partículas, em relação a quanto de fluido entrou no separador:
Outra forma de representar isso é usando concentração volumétrica; é o volume de partículas dividido pelo volume de suspensão, mas , certo?
Dividindo tudo por :
Daí:
Acabamos de ver uma forma de expressar a “concentração de fluido”. Daí também podemos escrever em função não da vazão de fluido, mas direto da vazão total:
O importante da razão de fluido é que ela funciona como se tivesse um T na tubulação, tipo, é como se ele dividisse a corrente em uma parte que é como se não passasse pelo separador (como se fosse um by-pass) e outra parte () que passa.
Agora, embora o seja uma medida para o fluido, pensa só nessa situação: se , significa que do fluido meio que ultrapassa o separador, certo? Mas esse fluido NÃO vai olhar as partículas dele e falar “Saiam daqui! Entrem no separador enquanto eu o ultrapasso”.

Ou seja, esse fluido que “ultrapassa” o separador vai levar, com ele, as partículas nele contidas, com a distribuição/concentração iqual a da entrada do equipamento. Então, se , é como se de suspensão já fosse direto pro concentrado e você pode afirmar que pelo menos das partículas vão ser separadas. Daí a razão de fluido garante uma eficiência mínima de coleta iqual a , ou seja, pra esse caso que te falei, a eficiência mínima vai ser .
Eficiência total REDUZIDA
Quando há no equipamento, a eficiência total vai meio que ser mascarada; vai ter uma parte de partículas que foi coletada pelo equipamento em si e outra parte que foi coletada pelo efeito T gerado pelo .
A eficiência total reduzida é uma medida da eficiência do equipamento em si, desconsiderando o efeito T da razão de fluido. A partir de , ela pode ser calculada por:
Eficiência granulométrica (ou individual por tamanho de partícula
Muitas vezes não vamos ter a informação da eficiência total direto e vamos ter que calculá-la baseado na distribuição da alimentação; com o que temos até agora ainda não conseguimos fazer isso, mas se soubermos a eficiência para cada diâmetro, conseguimos prever um comportamento para a amostra como um todo.

Então bora lá. A eficiência granulométrica é definida como a massa de um dado diâmetro recuperada em relação a massa desse diâmetro que entrou:
Só que:
Daí a gente chega em:
“Cortando” os :
Essa fórmula usamos se tivermos as curvas e . Se, por exemplo, for e:
Daí, derivando:
E a expressão para em função de para esse exemplo fica:
Voltando aos casos gerais, as curvas tem mais ou menos esse formato de “S” aqui:
- caso
- caso
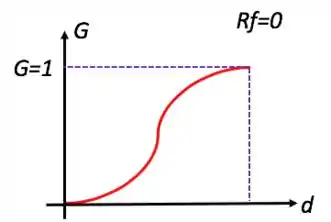
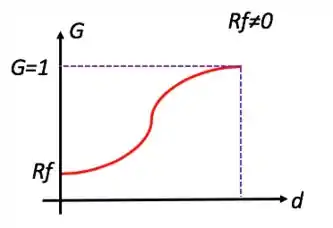
Duas coisas bemmm importantes que eu quero que você repare dessas curvas:
- é (e tem que ser!) no máximo igual a ; isso porque você não pode recuperar mais partículas do que alimenta
- Quando tem razão de fluido , ele garante eficiência mínima igual a ela para todas as curvas; isto é, é, no mínimo, igual a
Ah! Uma definição importante e que vai aparecer muitooooo daqui pra frente:
Cálculo de sabendo
Lembra que eu te falei que sabendo a eficiência para cada diâmetro íamos conseguir achar a eficiência para a amostra como um todo? A curva vai nos dizer qual a eficiência para um dado diâmetro; se considerarmos todos os diâmetros, podemos unir as contribuições deles e calcular a eficiência global . Fazemos isso com essa integral aqui:
Guarda essa expressão com carinho porque vamos usar bastante haha
Algo importante é que temos em função de , mas vamos integrar em daí vamos ter que colocar em função de . Tipo, se, por exemplo, a curva for descrita por:
Podemos, nesse caso, elevar os dois lados ao quadrado e multiplicar em X par isolar :
Eficiência granulométrica reduzida
Da mesma forma que existe eficiência total reduzida , existe eficiência granulométrica reduzida . A motivação é a mesma: querer medir a eficiência granulométrica do aparelho em si quando há razão de fluido. Calculamos por:
Quando trabalhamos com , podemos calcular por:
Equipamentos de separação em série
Para finalizar esse capítulo só falta falar de equipamentos de separação em série. Às vezes, a quantidade de partículas que você recupera em um equipamento de separação não é suficiente pra você; daí colocamos um segundo equipamento de separação para aumentar essa recuperação. A questão é que o que alimenta o segundo equipamento é a corrente diluído do primeiro (que é, geralmente, o overflow).
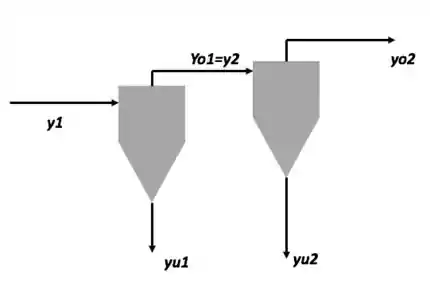
Além de poder olhar para cada equipamento isoladamente, que já aprendemos ao longo do capítulo, podemos olhar pra esse conjunto como uma coisa só:
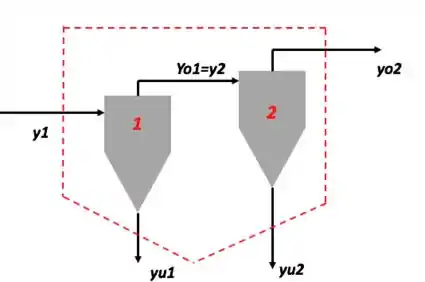
Chamando o primeiro equipamento de e o segundo de , podemos escrever a eficiência do conjunto como:
Só vamos usar essa forma se tivermos o e dados! Fora isso, vamos por .
Para a eficiência granulométrica é a mesma ideia:
Ou seja, essas fórmulas estão nos dizendo que a separação total do conjunto é o que é separado no primeiro equipamento somado ao que é separado no segundo, sendo que para o segundo só vai o que não foi separado no primeiro e, nesse segundo, essa corrente será separada com a eficiência do segundo equipamento .
E da mesma forma que podíamos escrever para o caso de um único equipamento, podemos escrever, para um conjunto:
Repara que usamos , ou seja, integramos com base no que entra no equipamento . Estamos considerando o conjunto como um equipamento único e a entrada dele tem distribuição né.
A vantagem, aqui, é que não precisamos saber a curva , então são menos cálculos.
Fica atento: se quiséssemos calcular , NÃO poderíamos usar a curva pra fazer porque é a entrada do primeiro separador e NÃO do segundo; por isso disse que só iriamos por se já tivéssemos e , senão é bem mais complicado.
Razão de fluido ( R f )
Eficiência total REDUZIDA E T '
Eficiência granulométrica (ou individual por tamanho de partícula G
Eficiência granulométrica reduzida G '
Equipamentos de separação em série
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Sabendo que a razão de fluido em um separador é e que a eficiência total reduzida do separador é , calcule a eficiência global de coleta.
Passo 1
Essa daí é só pra reforçar o conceito, aplicação de fórmula de cara haha
Sabemos que e que . A razão de fluido garante uma separação mínima (de valor igual ao de ) para todas as partículas; nos informa a eficiência do separador em si. Podemos calcular a eficiência global de coleta (que considera essas duas contribuições) por:
Substituindo os valores:
Isso faz sentido? SIMMM. A vazão associada com a razão de fluido é como se tivesse de coleta, já que ela carrega partículas com a mesma distribuição original e isso faz com que a eficiência global do separador aumente.
Resposta
Exercício Resolvido #2
Elaboração própria
Emum certo equipamento de separação, a curva pode ser escrita por:
Sabendo que a expressão para em função de (em ) na alimentação do separador é:
Calcule a eficiência global de coleta.
Passo 1
Primeiro de tudo, vamos entender porque essa curva de está dividida em dois intervalos. Lembra que eu disse lá na teoria que pode ser no máximo , já que você não pode recuperar mais do que alimenta? Então, mas a curva que descreve pode, em alguns casos, ultrapassar , já que ela é um simples ajuste matemático; nesses casos, a gente força no máximo estabelecendo uma fronteira: até o diâmetro em que por esse modelo matemático, calculamos pelo modelo matemático; para diâmetros maiores, .
Agora vamos ver o que a questão pede: temos e queremos a eficiência global de coleta, ou seja, . Vimos, la na teoria, uma fórmula que relaciona esses dois caras:
Só temos que prestar atenção porque, como é dividida em intervalos, essa integral também vai ser:
Em que ( “limite”) é o associado ao diâmetro de “fronteira”, diâmetro em que ocorre a divisão de ; nesse exemplo, esse diâmetro é . Jogando na fórmula de , achamos :
Daí:
Masssss, repara que tem um pra ser integrado e estamos integrando em ; precisamos, antes de integrar, escrever em função de .
Passo 2
Como:
Elevando os dois lados ao quadrado:
Isolando :
Substituindo isso naquela integral:
Resolvendo:
Resposta
Exercício Resolvido #3
Elaboração própria
Calcule a eficiência de um hidrociclone Rietma com base na seguinte fórmula pra :
Dados: , e sabe-se, também, como o diâmetro varia com :
Passo 1
O enunciado pediu pra gente calcular a eficiência; como ele não especifica, é a total . Pra chegar lá temos um caminho pra percorrer. Temos e a expressão para em função de . Daí temos tudo de . Podemos achar por:
Como o que queremos é , vamos usar:
Passo 2
Escrevendo em função de tudo que sabemos:
Para obter , precisamos resolver a seguinte integral:
Resolvendo na calculadora:
Como queremos , vamos ter que considerar a razão de fluido:
Como :
Resposta
Exercício Resolvido #4
Adaptado - Massarani, G. ( 2002 ). Fluidodinâmica em Sistemas Particulados, 2 a e d .
Deseja-se estudar o desempenho de uma bateria constituída por ciclones Lapple em série
com respectivamente e de diâmetro no tratamento de de gás contendo em volume de sólido.
Sabendo que as eficiências granulométricas de coleta de cada um dos dois ciclones podem ser escritas como:
Calcule a eficiência global de coleta do conjunto, sabendo que a distribuição da entrada do primeiro ciclone é:
Observação: todos os diâmetros estão em .
Passo 1
Essa questão fala de ciclones, que ainda não vimos! E agora!? Mas calma aí, repara que eu já escrevi as curvas de e o enunciado deu a curva pra então ainda não precisamos saber nada de ciclone pra resolver e achar essa eficiência global de coleta. Ufa! Haha
A gente só tem que lembrar que o que não é separado no primeiro equipamento é que vai para o segundo; a eficiência granulométrica total do conjunto pode ser escrita pela contribuição do que é separado no primeiro somado com a contribuição do que não foi separado no primeiro, mas foi no segundo; como vimos lá na teoria:
E, para calcular a eficiência global de coleta, podemos usar:
Lembrando que colocar em função de (ao invés de ), usando a curva da alimentação, já que esta é a entrada do conjunto.
Passo 2
Temos em função de , mas precisamos dele em função de para poder integrar. Usando a curva da alimentação, podemos escrever em função de e substituir em :
Manipulando:
Passo 3
Substituindo em função de em cada uma das expressões de :
Sabemos que
Daí, juntando tudo isso (NÃO SE ASSUTA! TEMOS CALCULADORA PRA NOS AJUDAR HAHA):
Agora, é só integrar:
Usando nossa amiga calculadora:
Resposta
Exercício Resolvido #5
Elaboração própria
Calcule a concentração volumétrica no concentrado de um hidrociclone que possui a seguinte curva :
Dado:
Passo 1
O exercício pede pra gente calcular a concentração volumétrica no concentrado; sabemos que concentração volumétrica é:
Como :
Foi nos dada a concentração volumétrica na entrada ; calculando a eficiência total de separação das partículas e levando em conta a concentração de entrada, podemos calcular qual o volume de partículas recuperado no concentrado.
Além disso, sabendo a razão de fluido, podemos calcular qual o volume de fluido que sai no concentrado; sabendo o volume de fluido e volume de partículas, podemos calcular a concentração no concentrado, que vou chamar de .
Ah! Não temos a vazão, né? Então bora falar que a vazão é .
Passo 2
Sabemos que:
Mas para resolver , precisamos colocar em função de ; já que temos uma curva de em função de , podemos isolar o , colocando-o em função de :
Para isolar , primeiro elevamos os dois lados a , que dá no mesmo que .
Substituindo na expressão de :
Agora sim podemos integrar:
expressa a parte das partículas que o equipamento em si recupera, mas como a razão de fluido, a eficiência global de separação vai ser maior do que isso, já que a vazão associada com a razão de fluido é como se tivesse de coleta (porque ela carrega partículas com a mesma distribuição original) e isso faz com que a eficiência global do separador aumente. Para obter :
Passo 3
Na entrada, , então dessa vazão são partículas e o resto é fluido.
Agora, vamos por partes:
- Sabemos que daí dessa vazão de partículas foi recuperada, ou seja:
- significa que do fluido alimentado sai no concentrado. Daí, junto com , sai:
Calculando :