Câmara de poeira
Produzido por Marcelo AlvesTeoria
Que rufem os tambores! Finalmente chegamos nos equipamentos de separação : ) Eles são o grande objetivo de tudo que estudamos até agora. Então bora lá!
Câmara de Poeira
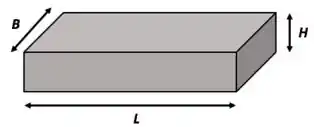
Esse é o equipamento mais simples que vamos ver. Ele é usado para separar partículas sólidas de um GÁS! De novo: separar partículas sólidas de um GÁS! É, simplesmente, uma caixa. Chamando de a altura, o comprimento e a largura:
Lembrando do tópico de escoamento, sabemos que na direção do movimento do fluido, a partícula caminha com a mesma velocidade do fluido e na direção do campo de força (que no caso aqui é o campo gravitacional) ela caminha com velocidade terminal. Então, a trajetória dela é tipo assim:
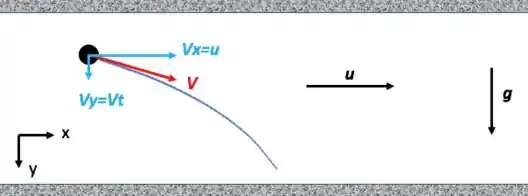
“Então você tá dizendo que a partícula vai pro chão?” Muita calma nessa hora! Não disse isso. A TENDÊNCIA é a partícula ir para o chão, mas a questão é que ela leva um certo tempo para descer até o chão e o tempo que ela fica dentro da câmara pode ou não ser suficiente para ela chegar no chão.
E qual é a importância de conhecer esse tempo? A partir deles conseguimos dimensionar a câmara de poeira! Já que o que queremos é que as partículas cheguem ao chão ANTES de atravessar a câmara. Porque assim conseguimos separar elas do gás.
Podemos partir da definição de velocidade que já conhecemos:
Daí:
Só que existem dois tipos diferentes de tempos que precisamos calcular para câmaras de poeira.
O primeiro deles é o tempo que ela leva pra chegar ao “chão” da câmara. Nosso querido tempo de queda.
Ou seja, a partícula percorre com a velocidade dela (puramente na direção y), gerada pelo campo gravitacional.
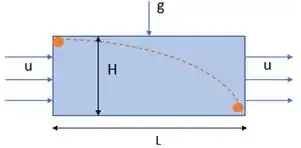
E o outro tempo é o tempo de residência, que nada mais é do que o comprimento da câmara () dividido pela velocidade da partícula na direção , que é a velocidade do fluido, .
Note que esse tempo também é igual à razão entre o volume da câmara () e a vazão de alimentação (). A vazão de alimentação () da câmara é o produto da velocidade do fluido (velocidade no eixo x) e área de entrada da câmara (HB).
E como dimensionaríamos essa câmara de poeira a partir dos tempos? Bem, vamos pensar numa partícula que entra láá bem pertinho do teto. No caso mais crítico, vamos recuperar ela no “último” milímetro da base da câmara. Isso significa que ela vai percorrer no mesmo tempo que vai percorrer . Logo, os tempos de queda e residência dessa fofa devem ser iguais.
Assim, pode ser calculado por:
Caso a vazão seja conhecida e sabendo que , podemos escrever essa equação da seguinte forma:
E tá relacionado com um diâmetro de partícula, né? Então, através desse a gente pode calcular o diâmetro daquela partícula que entrou na parte mais alta da nossa câmara e foi coletada lá no finalzinho. Esse cara, a gente vai chamar de ou .
Agora, se uma partícula tiver diâmetro igual a a gente sabe que ela vai ser coletada. Porque ou ela entra em e a gente viu que ela é coletada lá no final da câmara, ou ela entra mais embaixo, daí cai ainda mais rápido, então é coletada também.
Partículas maiores que também são 100% coletadas, porque tem a velocidade terminal ainda maior que a partícula de .
O que isso significa? Significa que toda partícula com diâmetro maior ou igual a será coletada com 100% de eficiência na nossa câmara de poeira!!!
E pra quem tem diâmetro menor que isso?

Vareia mesmo, titio Einstein.
Se o cara for menor e entrar em , ele não vai descer a tempo de ser coletado, porque vai ter menor que o nosso caso limite (aquele do ). Agora, ele também pode ser menor, mas, por entrar mais embaixo, ser coletado.
Pra saber se as outras partículas serão coletadas, temos que conhecer a eficiência da câmara de poeira.
Eficiência da Câmara de Poeira
Mas o que seria essa eficiência? Eficiência individual de coleta pode ser definida da seguinte forma:
E como definimos essa tal eficiência para partículas entrando em uma altura qualquer? A eficiência de coleta ou granulométrica ( para um dado diâmetro de partícula é a razão da altura que a partícula realmente entrou (y) e a altura da caixa (H).
E, como para qualquer posição de entrada podemos igualar os tempos de queda e residência, obtemos outra fórmula para eficiência:
Logo, a curva de eficiência granulométrica por diâmetros possui a seguinte forma:
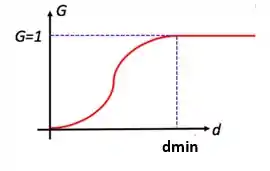
Repara que depois de , todos os diâmetros têm já que são recuperados.
O lance é que sabemos que tem que ser no máximo 1, e essa equação permite . Daí, impomos um limite e vamos ter a equação de para a câmara de poeira:
Só um detalhe: saber esse porquê de ter essa definição em intervalos para na câmara de poeira é importante; já vi aparecer em questão teórica em prova.
Diâmetro de Corte
A gente já definiu como diâmetro mínimo pras partículas serem coletadas com 100% de eficiência. Agora vamos definir o diâmetro de corte, ou , que é o diâmetro das partículas que são coletadas com 50% de eficiência.
E esse pode nos ajudar a simplificar algumas equações. A eficiência da câmara, por exemplo, pode ser expressa assim:
Atenção! Isso aí só é válido se assumirmos que as partículas sedimentam na região de Stokes (regime laminar né). E presta atenção que os “limites de validade” da função seguem em relação ao e não a .
E a relação existente entre e é:
Pra guardar no coração!
Algumas recomendações
Quando tivermos mais de uma solução possível para nossos problemas, mais de uma câmara de poeira possível de projetar, usamos as recomendações de Svarovsky (E não! Não é o mesmo dos cristais haha):
- Teto quadrado, isto é,
- Quando você não tiver nenhuma informação de , use . Caso contrário, use o que o problema der né.