Extração em corrente cruzada
Produzido por Marcelo AlvesTeoria
Introdução
Oi oi oii, agora vamos falar um pouco sobre o processo da extração em corrente cruzada que também pode ser chamada de extração por contato múltiplo com solvente! Esse modo de operação é usado preferencialmente em operação por batelada e é representado da seguinte forma.
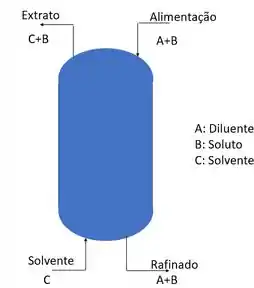
Nessa situação o solvente puro tem contato continuamente com a alimentação. Na qual p soluto é progressivamente removido e o refinado é altamente purificado, fazendo com que o extrato saia rico em soluto (componente de interesse).
Balanço de massa
Para fazer o balanço de massa vamos colocar adicionar uma letra para cada corrente para facilitar nossa vida, beleza?

Fazendo o balanço de massa ficamos então com,
Em que e são as frações em massa do soluto na alimentação, no rafinado, no solvente e no extrato respectivamente.
Considerações especiais
Assumindo-se:
- Imiscibilidade da alimentação e do solvente
- O solvente inicial não contém soluto, isto é e e usando a relação de equilíbrio , temos:
Ou razão de redução,
Assumindo que o coeficiente de partição é constante para todo o intervalo de concentrações e que a quantidade de solvente em cada um dos estágios é a mesma, ou seja,
E a quantidade de solvente requerida é:
Ou razão de redução,
Reta de operação e número de estágios
A reta de operação vai ser:
Já a determinação do número de estágios pode ser tanto pelo método gráfico, através da construção de McCabe Thiele usando a curva de equilíbrio e a reta de operação. Quanto pelo método de Kremser, sendo nesse caso para concentrações inferiores a 1%.
Agora vamos exercitar!!

Balanço de massa
Considerações especiais
Reta de operação e número de estágios
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Descreva o processo de extração em corrente cruzada.
Passo 1
Heyyy, turubom? Vamos falar um pouco sobre o processo da extração em corrente cruzada que também pode ser chamada de extração por contato múltiplo com solvente, que é isso que o enunciado quer, beleza?
Passo 2
Esse modo de operação é usado preferencialmente em operação por batelada e é representado da seguinte forma.
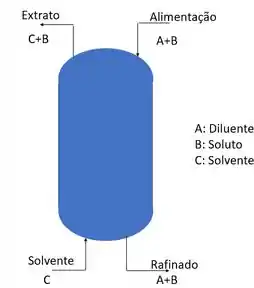
Nessa situação o solvente puro tem contato continuamente com a alimentação. Na qual o soluto é progressivamente removido e o refinado é altamente purificado, fazendo com que o extrato saia rico em soluto (componente de interesse).
Resposta
Nessa situação o solvente puro tem contato continuamente com a alimentação. Na qual o soluto é progressivamente removido e o refinado é altamente purificado, fazendo com que o extrato saia rico em soluto (componente de interesse).
Exercício Resolvido #2
Elaboração própria
Deduza o balanço de massa de uma coluna com extração em corrente cruzada.
Passo 1
Fala aíii, tudo bem? Temos que a coluna é:
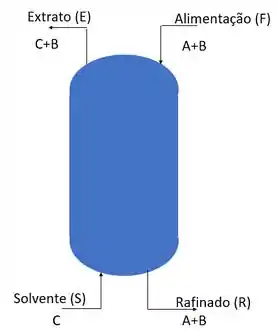
Passo 2
Fazendo o balanço de massa ficamos então com,
Em que e são as frações em massa do soluto na alimentação, no rafinado, no solvente e no extrato respectivamente.
Resposta
Exercício Resolvido #3
Elaboração própria
Deduza o balanço de massa de uma coluna com extração em corrente cruzada assumindo-se imiscibilidade da alimentação e do solvente e que o solvente inicial não contém soluto.
Passo 1
Oi oi oii, tudo show de bola? Nessa questão nós vamos fazer o balanço de massa da coluna com algumas considerações especias.
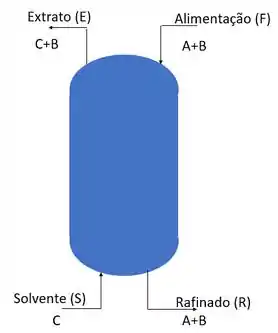
A primeira consideração que vamos assumir é a imiscibilidade da alimentação e do solvente e a segunda é que o solvente inicial não contém soluto. Ou seja,
Passo 2
Fazendo o balanço de massa ficamos com,
Em que e são as frações em massa do soluto na alimentação, no rafinado, no solvente e no extrato respectivamente.
E usando a relação de equilíbrio , temos:
Que também podemos chamar de razão de redução no seguinte formato,
Resposta
Exercício Resolvido #4
Elaboração própria
Tendo a razão de redução em mãos, assuma que o coeficiente de partição é constante para todo o intervalo de concentrações e que a quantidade de solvente em cada um dos estágios é a mesma.
O que essa consideração irá influenciar na razão de redução?
Passo 1
Heyyy, tudo bem? Nessa questão nós vamos manipular a razão de redução,
Assumindo que o coeficiente de partição é constante para todo o intervalo de concentrações e que a quantidade de solvente em cada um dos estágios é a mesma. Ou seja,
Passo 2
Com isso temos que a quantidade de solvente requerida é,
E a razão de redução será,
Resposta
Exercício Resolvido #5
Elaboração própria
Considere uma extração líquido-líquido em uma coluna com 5 estágios. Sabendo que o coeficiente de partição é constante para todo o intervalo de concentrações e que a quantidade de solvente em cada um dos estágios é a mesma, calcule a razão de redução dado .
Passo 1
Heyyy, tudo bem? Primeira coisa que nós vamos fazer aqui é identificar o que o enunciado nos forneceu. Ele nos deu:
E nos pediu a razão de redução. Ou seja,
Passo 2
Substituindo os valores dados na equação da razão de redução temos,
Logo, a razão de redução é:
Resposta
Exercício Resolvido #6
Adaptado – Problema 6, Extração líquido-líquido, Operações Unitárias II, Prof. Roberto de Sousa Gomes da Silva, FURG
Uma vazão de de uma mistura aquosa contendo (em massa) de ácido acético é alimentada no primeiro estágio de um extrator de dois estágios, utilizando-se como solvente éter isopropilico contendo (em massa) de ácido acético. O solvente é alimentado a uma vazão de em fluxo cruzado em cada estágio. Se a extração ocorre a e . Determine as composições das correntes de extrato e de refinado que saem do extrator;

Passo 1
Oiii, tudo certinho? Nessa questão nós temos uma extração líquido-líquido em fluxo cruzado com as seguintes informações:
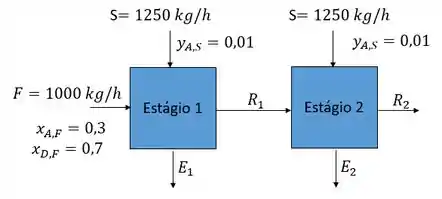
A partir disso queremos determinar as composições das correntes de extrato e de refinado que saem do extrator. Então vamos lá!
Passo 2
Para esse problema vamos analisar o primeiro estágio como se estivéssemos lidando com um estágio único, beleza? Logo,
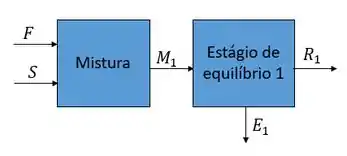
Vamos inicialmente calcular a vazão da mistura fazendo o balanço geral no misturador 1:
Agora precisamos definir qual é a composição dessa mistura. Fazendo o balanço por componente.
Passo 3
Para o soluto temos,
Para o solvente temos,
Para o diluente temos,
Passo 4
Temos que está sobre a reta e vai gerar e ao atingir o equilíbrio.

Agora que descobrimos precisamos encontrar a reta que vai passar pelo ponto e vai gerar o extrato e o refinado.
Passo 5
Para isso vamos utilizar a curva rebatendo um ponto aleatório da curva a linha conjugada obtendo,
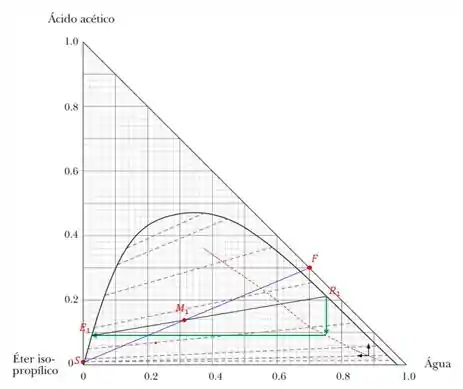
Fazendo a leitura desse gráfico vemos que a composição do extrato é,
E do rafinado é,
Resposta
A composição do extrato é,
E do rafinado é,
Exercício Resolvido #7
Adaptado – Problema 6, Extração líquido-líquido, Operações Unitárias II, Prof. Roberto de Sousa Gomes da Silva, FURG
Uma vazão de de uma mistura aquosa contendo (em massa) de ácido acético é alimentada no primeiro estágio de um extrator de dois estágios, utilizando-se como solvente éter isopropilico contendo (em massa) de ácido acético. O solvente é alimentado a uma vazão de em fluxo cruzado em cada estágio. Se a extração ocorre a e . Determine as vazões das correntes de extrato e de rafinado que saem do extrator.

Dados:
Passo 1
Oiii, tudo certinho? Nessa questão nós temos uma extração líquido-líquido em fluxo cruzado com as seguintes informações:

Além disso, temos:
Com isso vamos determinar as vazões das correntes de extrato e de rafinado que saem do extrator. 😉
Passo 2
Vamos analisar um estágio de cada vez como se estivéssemos lidando com estágios únicos, beleza? Então vamos começar olhando para o nosso primeiro estágio:
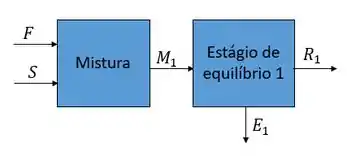
Vamos inicialmente calcular a vazão da mistura fazendo o balanço geral no misturador 1:
Passo 3
Com fazer um balanço global no estágio de equilíbrio 1 e encontrar,
Fazendo agora um balanço do soluto temos,
Voltando no balanço global temos,
Passo 4
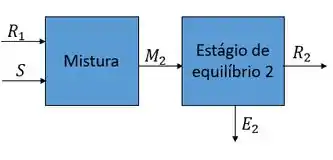
Trabalhando agora com o segundo estágio, ou seja,
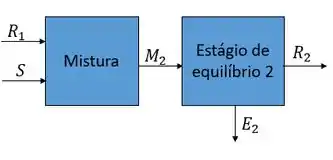
Podemos fazer o balanço global e obter,
Fazendo o balanço por componente para o soluto,
Para o diluente temos,
Para o solvente temos,
Passo 5
Temos que está sobre a reta e vai gerar e ao atingir o equilíbrio. Depois vamos utilizar a curva rebatendo um ponto aleatório da curva a linha conjugada obtendo,
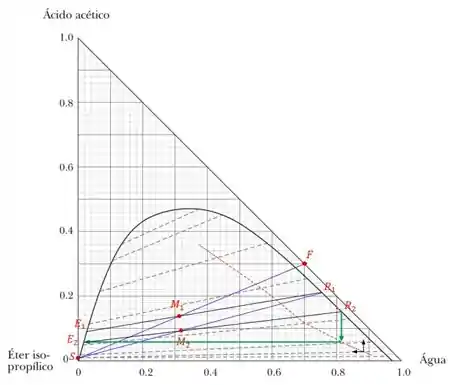
Fazendo a leitura desse gráfico vemos que a composição do extrato é,
E do rafinado é,
Passo 6
Agora vamos fazer um balanço global no estágio de equilíbrio 2,
Fazendo o balanço por componente com o soluto,
Substituindo no balanço global temos,
Resposta
Exercício Resolvido #8
Adaptado, Operações Unitárias 2, Escola de Química/UFRJ, Lista 8 2017.1 – Extração Líquido – Líquido
O dioxano presente em de uma solução aquosa com em massa de dioxano deve ser extraído com de benzeno puro a . Admita que o benzeno e a água são insolúveis. Determine a corrente do rafinado e a porcentagem de dioxano extraída pelo benzeno considerando um estágio de equilíbrio.
Dados de Equilíbrio líquido – líquido a e .
Passo 1
Fala aiii, tudo certinho? Nessa questão nós temos uma coluna com benzeno e água com um estágio de equilíbrio. Esquematicamente temos,
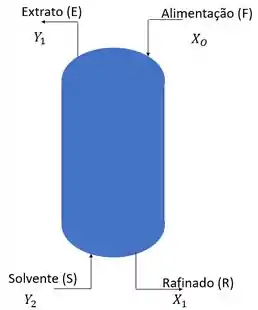
Onde nos foi dado a alimentação,
Com,
E a corrente do solvente,
Com,
Além de,
E com isso vamos determinar a corrente do rafinado e a porcentagem de dioxano extraída pelo benzeno considerando um estágio de equilíbrio. Ou seja,
Passo 2
Precisamos encontrar rafinado, mas antes, considerando que o benzeno e a água são insolúveis, podemos tratar a coluna como de esgotamento. Logo a corrente líquida é,
Substituindo os valores,
Passo 3
E a corrente vapor é representada por,
Porém,
Pois o solvente é líquido.
Para corrente do rafinado vamos usar,
Lembrando que o enunciado nos forneceu que,
E substituindo os valores temos,
Passo 4
Já para o extrato temos,
Logo a a porcentagem de dioxano extraída pelo benzeno é,