Distribuição Amostral da Média
Produzido por Jorge Alberto NascimentoTeoria
Fala meu querido!!! Digamos que um pesquisador quer saber qual é a altura média dos brasileiros. Ele trata isso como uma v.a. que a gente vai chamar de . Para encontrar essa média, ele não vai medir a população toda, mas só uma amostra.
Imagina que ele fixou o tamanho da amostra em pessoas. Ele foi lá e mediu a altura dessas 40 pessoas e teve um valor pra média amostral de . Só de curiosidade, ele resolveu mais uma vez tirar uma outra amostra do mesmo tamanho, repondo as pessoas que foram utilizadas na primeira amostra. Na segunda vez ele teve um valor pra média amostral de .
Imagina que ele ficou repetindo esse processo de amostrar várias vezes... Podemos ilustrar da seguinte forma:
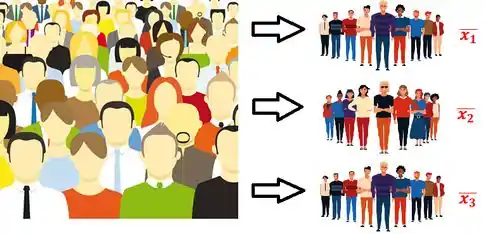
Para cada amostra que ele faz, ele tem um valor específico pra média amostral (e aleatório, porque antes de tirar as medidas, ele não sabe qual valor vai sair). Como esse valor é aleatório, a gente chama essa v.a. de média amostral e a distribuição dessa v.a.a a gente chama de distribuição amostral da média. Beleza?!
Tá... Beleza, mas digamos que temos o seguinte cenário: Sabemos que a média populacional é e desvio padrão e não conhecemos a distribuição da estatura da população.
Diante disso, alguém pede pro pesquisador selecionar uma amostra com 40 pessoas e calcular a probabilidade da média amostral ser maior ou igual que Como ele pode calcular isso?

Mas peraeeeee!!!!! Antes de resolvermos o problema anterior, é importante entendermos como funciona esse lance da distribuição amostral das médias...
Para isso precisamos voltar no Teorema Central do Limite. Você não lembra dele? Ele diz que não importa qual é a distribuição , a distribuição de sua média se aproxima da normal à medida que o número de amostragem cresce (desde que a média e a variância existam).
Visualizando graficamente seria algo dese tipo:
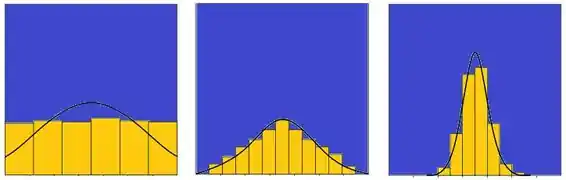
Ou seja,
IMPORTANTE!!! No nosso probleminha o pesquisador está repondo os carinhas utilizados na amostra!!
Com Reposição
Como conhecemos os parâmetros da população, conseguimos estimar os parâmetros das médias amostrais :
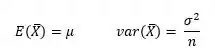
Então, teremos
Beleza?!
Assim, temos que a nossa distribuição amostral das médias vai ter uma carinha parecida com essa aqui:
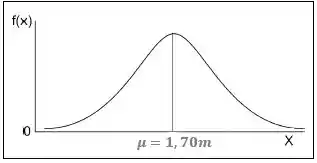
Onde a curva estará centrada na média populacional com desvio padrão de
Nós queremos calcular a probabilidade da média da amostra selecionada ser maior ou igual a . Ou seja, queremos calcular , que seria a área pintada de azul na figura abaixo:
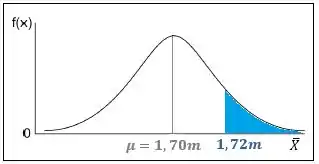
Belezinha?!
Se você parar pra pensar, a nossa variável não será mais a estatura nesse caso. A nossa variável agora é a média amostral, que vamos denotar por .
Agora nós vamos realizar aquele processo de padronizar! No processo de padronização teremos uma pequena diferença do que estamos acostumados:
Onde é o desvio padrão das médias.
No nosso problema, teremos
Beleza?!
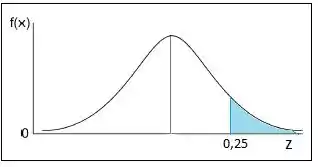
Procurando na tabela e fazendo as continhas, teremos
Show de bola?!
Tá bom.. mas no problema o pesquisador realiza a reposição dos carinhas utilizados na amostra. E se não tivesse essa reposição????

Calma meu pimpolho!! Vamos ver isso agora!!
Sem Reposição
Se não tiver a reposição isso mudará a probabilidade de cada elemento pertencer a amostra. Isso vai influenciar no cálculo do desvio padrão das médias:
Dessa forma, as formulinhas mudarão um pouco:
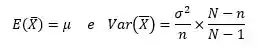
Onde é o número de elementos da população.
Então digamos que nossa população seja de 300 pessoas. No nosso problema teremos:
Agora o procedimento é o mesmo! Padronizando,
Assim,
Beleeeza?!
Nos vemos nos exercícios!!!

Com Reposição
Sem Reposição
Exercícios Resolvidos
Exercício Resolvido #1
CEFET-Prof Anna Regina
A média e a variância de uma população equiprovável, cujos possíveis valores são os inteiros 1, 2, 3 e 4, são e . Considere a distribuição amostral de para amostras de elementos e determine sua média e variância, supondo a população finita formada por 12 elementos e amostragem com reposição.
Passo 1
Temos os dados da população.
E temos que calcular a média e a variância da distribuição amostra de , para uma amostra com:
Passo 2
A gente sabe que, como estamos tratando de amostras retiradas com reposição. O valor da média e da variância serão:
Então..
Resposta
Exercício Resolvido #2
CEFET-Prof Anna Regina
A média das notas obtidas na disciplina de Estatística num determinado curso de graduação tem sido igual a 7,7 e a variância igual a 1,96. Caso sejam extraídas várias amostras de 49 alunos cada uma, do total de 586 que estão matriculados na disciplina, determine o desvio padrão da distribuição amostral das médias, levando-se em conta que a amostra foi efetuada:
- Com reposição;
- Sem reposição.
Passo 1
Temos os dados da nossa população de notas de alunos em Estatística:
E temos que calcular o desvio padrão da distribuição amostral das médias para dois casos, sendo que sabemos que nossa amostra tem 49 alunos:
E lembrar que:
Passo 2
(a)
Para o caso de ser com reposição a amostragem, a gente tem que:
Com isso:
Passo 3
(b)
Para amostragem sem reposição:
Substituindo os valores: