Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 45
De acordo com reportagens publicadas, a prática sob condições de fadiga distorce os mecanismos que governam o desempenho. Um experimento foi conduzido, utilizando 15 estudantes universitários do sexo masculino que foram treinados para fazer um movimento contínuo horizontal com o braço, da direita para a esquerda, de uma microchave para uma barreira, batendo sobre a barreira coincidentemente com a chegada do ponteiro de um relógio na posição de 6 horas. O valor absoluto da diferença no tempo, em milissegundos, que levou para que houvesse o toque na barreira e no tempo que levou para que o ponteiro chegasse às 6 horas (500 ms) foi registrado. Cada estudante realizou a tarefa cinco vezes sob condições de pré-fadiga e pós-fadiga, e as somas das diferenças absolutas para as cinco performances foram registradas a seguir:

Um aumento na média das diferenças absolutas dos tempos quando a tarefa foi realizada pós-fadiga apoiaria a afirmação de que a prática sob condições de fadiga distorce os mecanismos que governam o desempenho. Assumindo que as populações são normalmente distribuídas, teste essa afirmação.
Passo 1
Selvaaaaaaaaaa galerinha, isso mesmo selva haha, tudo certinho??
“Hulk esmaga”, Bora esmagar essa questãozinha comigo?

Os dados a seguir mostram a diferença média absolutas para os 15 homens.

Reivindicação: Um aumento nas diferenças médias absolutas de tempo quando a tarefa é executada em condições de pós-fadiga apoiaria a alegação de que a prática sob condições de fadiga distorce os mecanismos que governam o desempenho.
O teste de duas médias pode ser realizado quando os dados estão na forma de observações pareadas.
Assim, podemos aplicar o teste t pareado.
Agora organizamos o procedimento de teste e os cálculos são fornecidos abaixo.
Procedimento:
Este problema de duas amostras é essencialmente reduzido a um problema de uma amostra usando as diferenças calculadas .
Assim, a hipótese reduzida a
Portanto
Como não foi fornecido o nível de significância, vamos usar
Regra de decisão: Rejeitar
Passo 2
A estatística de teste computada é então dada como
A região crítica é construída usando a distribuição t com graus de liberdade.
Passo 3
Para encontrar a esta a estatística de teste, usaremos a tabela a seguir
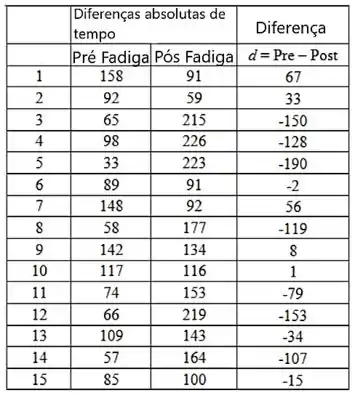
Passo 4
Agora iremos determinar a média e o desvio padrão para as diferenças
Agora, calcularemos a estatística de teste para o teste t pareando da seguinte maneira
Assim, o valor da estatística de teste t é de .
Passo 5
Graus de liberdade
Partindo dessa afirmação declarada, podemos ver que o teste é direcional (a cauda para a esquerda)
Agora, vamos calcular o valor P para o teste de cauda esquerda
O valor P do teste é 0,0121, que é menor que 0,05.
Assim, rejeite a hipótese nula a um nível de significância de 5%.
Há evidências suficientes para apoiar a afirmação de que há um aumento na diferença média absoluta de tempo quando a tarefa é realizada em condições de pós-fadiga.
“OK, isso foi legal.”

Resposta
Resposta nos passos.