Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.3 - Ex. 2
Uma amostra com 10 observações de uma variável aleatória Normal forneceu média de 5,5 e variância amostral 4. Deseja-se testar, ao nível de significância de , se a média na população é igual ou é menor do que 6. Qual é a conclusão?
Passo 1
Temos então, uma variável aleatória normalmente distribuída; e:
Como não conhecemos a variância populacional, podemos utilizar a seguinte aproximação:
Passo 2
Como dito no enunciado, estamos buscando o seguinte teste:
Para isso precisamos de uma região crítica, ela é definida assim:
Como essa região é unilateral, então devemos buscar a seguinte coluna na tabela t-student:
E na linha 9 graus de liberdade.
Encontramos o seguinte:
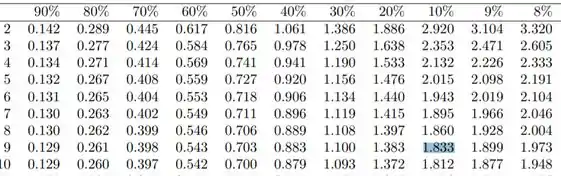
Portanto a nossa região crítica será:
Passo 3
Agora, só falta realizar o teste sob
Portanto, não pertence à nossa região crítica; então NÃO devemos rejeitar
Resposta
Podemos concluir que existem evidências de que a média seja igual a 6.