Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.3 - Ex. 1b
Com o auxílio da tabela calcule:
(b)
Passo 1
Mais uma vez, lembrando que a tabela de t-student nos fornece valores cuja probabilidade de:
E como esse limite é BILATERAL, podemos dizer que:
Passo 2
Na letra B, vamos ter que abrir esse módulo ai né
Lembrando que:
Vamos fazer isso então:
Se você reparar, que , então:
Então vamos buscar esse na tabela.
Passo 3
Para isso, vamos buscar na linha 8 (graus de liberdade) um valor e olhar a coluna em que ele está:
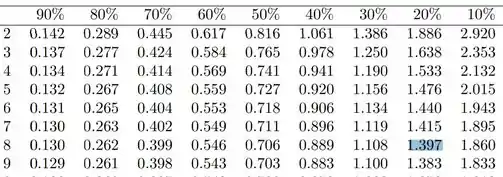
Repare então, que:
E portanto:
Resposta
(b)
Exercícios de Livros Relacionados
Com o auxílio da tabela t - s t u d e n t calcule:(g) O valor de d tal que P t 2 1d = 0 , 05
Uma amostra com 10 observações de uma variável aleatória Normal forneceu média de 5,5 e variância amostral 4. Deseja-se testar, ao nível de significância de 5 % , se a média na população é igual ou é
Admitindo que a pressão sanguínea arterial em homens siga o modelo Normal, 7 pacientes foram sorteados e tiveram sua pressão medida com os seguintes resultados: 84 ; 81 ; 77 ; 85 ; 69 ; 80e79 . Determ
Admitindo que a pressão sanguínea arterial em homens siga o modelo Normal, 7 pacientes foram sorteados e tiveram sua pressão medida com os seguintes resultados: 84 ; 81 ; 77 ; 85 ; 69 ; 80e79 . Teste
O tempo de permanência de engenheiros recém formados no 1ºemprego, em anos, foi estudado considerando um modelo Normal com média e variância desconhecidas.Por analogia com outras categorias profission