Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios Suplementares - Ex. 88
Os dados a seguir referem-se à contagem de bactérias transportadas pelo ar (número de colônias/pés3 ) para m 8 quartos de hospital atapetados e para n 8 quartos sem tapete ("Microbial Air Sampling in a Carpeted Hospital", J. Environmental Health, 1968, p. 405). Parece haver diferença na contagem média real de bactérias entre os quartos atapetados e os não-atapetados?
Suponha que você soube depois que todos os quartos atapetados estavam em um hospital de veteranos de guerra, enquanto todos os quartos não-atapetados estavam em um hospital infantil. Você seria capaz de avaliar o efeito da existência ou não do tapete? Comente.
Passo 1
Temos que m=8e n=8 são tamanhos de amostra, e que são variáveis aleatórias independentes e identicamente distribuídas com média e desvio padrão , ambos desconhecidos (estes representam a contagem de bactérias para quartos de hospital acarpetados).
Também nos é dado que são variáveis aleatórias independentes e identicamente distribuídas com média e desvio padrão , ambos desconhecidos (estes representam a contagem de bactérias para quartos de hospital sem carpete).
Além disso, X e Y são amostras independentes (portanto, todos os são independentes de todos os ).
Queremos testar:
ao nível de significância (nossa escolha).
Primeiro precisamos verificar a suposição de normalidade para ambas as amostras, e para isso vamos desenhar um gráfico de probabilidade normal.
Este gráfico plota as observações ordenadas versus os quantis normais, que são na verdade valores , para todo , onde é a função de distribuição cumulativa de uma variável aleatória normal padrão, e é sua função inversa.
Usamos o software estatístico R para desenhar o gráfico de probabilidade normal. Por exemplo, o comando
qqnorm(x)
irá desenhar o gráfico desejado, que é mostrado na imagem abaixo.
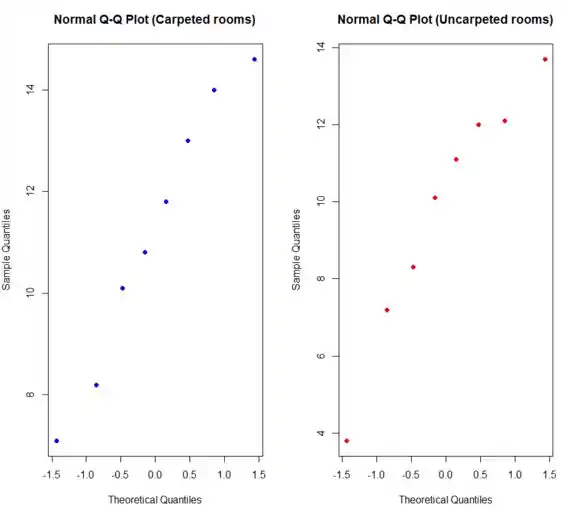
Ambos os gráficos mostram retidão e não temos motivos para rejeitar a hipótese de normalidade (também, os tamanhos das amostras são muito pequenos para poder rejeitar essa hipótese com alguma confiança, mesmo que alguma curvatura fosse aparente).
Em outras palavras, podemos assumir que nossas amostras são distribuídas aproximadamente normalmente.
Aqui está o gráfico:
Passo 2
A estatística de teste usada para testar as hipóteses acima é
que, sob a hipótese nula, segue a distribuição t com graus de liberdade, onde é calculado como
As médias amostrais podem ser calculadas como
Os desvios padrão da amostra são então
E
Assim, o número de graus de liberdade é
Então, substituindo todos os valores, (este é o valor nulo, ou seja, o valor assumido na hipótese nula) na fórmula acima produz o valor da estatística de teste:
Como o teste é bicaudal, então o valor P deste teste é
onde t denota o valor observado da estatística de teste.
Para encontrar aproximadamente este valor de P, consultamos a tabela A.5 nas Tabelas do Apêndice. Na linha rotulada (esses são os graus de liberdade), encontramos o valor mais próximo de t=0.954 (apenas um, pois 0.954 é menor que qualquer valor nessa linha). Esse valor é = 1. 350 e é menor que esse valor, o que significa que é maior que 0.10, então podemos concluir que
Passo 3
Para encontrar o valor exato de PP, podemos usar algum software. Uma linha
no software estatístico R relatará o valor P, que acaba sendo
Como o valor PP deste teste é maior que nosso nível de significância α=0.05, então falhamos em rejeitar a hipótese nula, ou seja, não podemos rejeitar a afirmação de que a contagem média de bactérias da população é a mesma para quartos de hospital com carpete e sem carpete.
Depois de obtermos essas novas informações, não seríamos capazes de avaliar o efeito do carpete - − pode ter havido alguns fatores de confusão que podem ter contribuído para a significância estatística (salas aleatórias remover um pouco esses fatores).
Resposta
O valor da estatística de teste é T=0.954 com o valor P de 0.3575, então não rejeitamos a hipótese nula