Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 6
Dois tetraedros (dados com quatro faces) com as faces numeradas de um a quatro são lançados e os números das faces voltadas para baixo são anotados. Sejam as v.a.:
X: maior dos números observados;
Y: menor dos números observados;
Z = X + Y.
(a) Construa a tabela da distribuição conjunta de X e Y.
(b) Determine as médias e as variâncias de X, Y e Z.
Passo 1
(a) Construa a tabela da distribuição conjunta de X e Y.
A primeira coisa que devemos fazer é determinar o nosso espaço amostral.
Passo 2
Lembrando que X: maior dos números observados e Y: menor dos números observados.
Como cada resultado é equiprovável, obtém-se
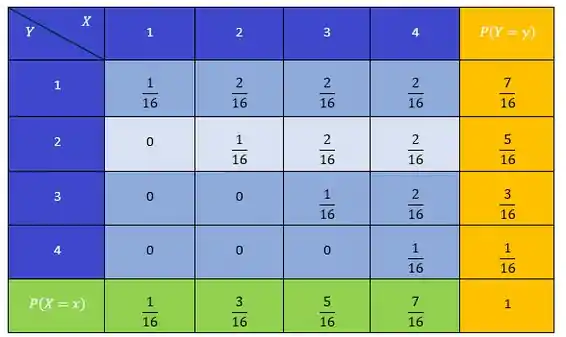
Passo 3
(b) Determine as médias e as variâncias de X, Y e Z.
Primeiro, vamos construir uma tabela com os valores de ?
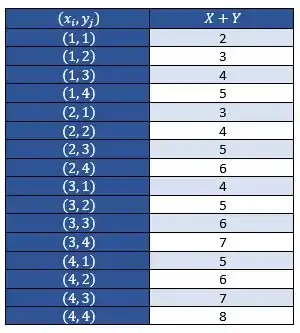
Estão faltando as probabilidades, né?
Vamos calcular um exemplo?
Seguindo o mesmo raciocínio, podemos calcular as outras probabilidades. Dessa forma, podemos montar a nossa tabela da distribuição de .
Passo 4
Sabemos que
Portanto
Para o cálculo da precisamos lembrar da seguinte fórmula:
Portanto, precisamos calcular , e
Substituindo nas fórmulas, temos:
Resposta
(a)
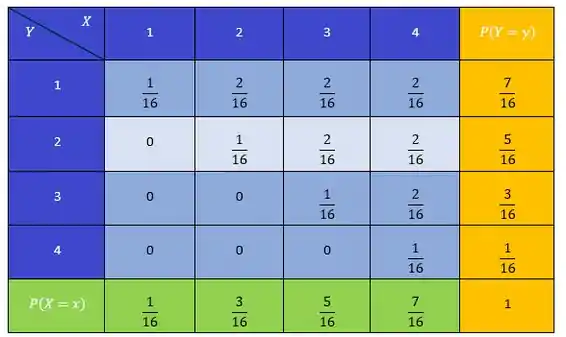
(b)