A New England Insurance Company está revendo os hábitos de direção das mulheres na faixa entre 16 e 24 anos, para determinar se elas devem continuar pagando prêmios de seguro mais elevados do que as mulheres de outras faixas etárias. Em um estudo de 750 mulheres motoristas selecionadas aleatoriamente na faixa etária 16-24, a distância média percorrida em um ano é de 6047 mi, com desvio-padrão de 2944 mi (com base em dados da Federal Highway Administration). Ao nível de 0,01 de significância, teste a afirmação de que a média populacional para as mulheres com 16-24 anos é inferior a 7124 mi, que é a média conhecida para as mulheres de idade mais alta. Se as mulheres na faixa 16-24 dirigem menos, deveriam elas pagar prêmios de seguro menores? Identifique também o valor P.
Passo 1
Tudo certo, galera? Bora continuar a fazer mais uns exercícios de teste de hipótese! São vários passos, mas não precisa ter medo! É só repetir o processo que estávamos fazendo! Vamos ter que usar uma tabela de distribuição normal de novo! Trouxe aqui uma imagem dela pra vocês!
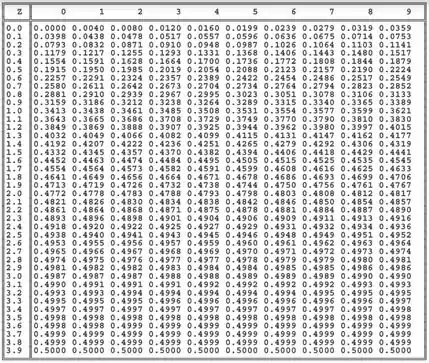
Também vamos precisar usar a fórmula do Z para um Teste de Hipóteses para média (com conhecido ou ):
Primeiro, vamos determinar os valores iniciais do problema, montando e (já sabemos que o teste será unilateral esquerdo porque vamos testar a hipótese ):
Passo 2
Beleza! Agora temos que encontrar o Z a partir da fórmula de antes:
Em seguida, chegamos ao valor P () correspondente ao Z encontrado na tabela, já que buscamos a seguinte situação:
Vish! De novo isso! O valor de que encontramos é muito grande em módulo, então vamos ter que assumir o valor correspondente de 0,5 nessa situação! Assim, chegamos a .
Passo 3
Estamos no final! Agora, para acabar o teste de hipóteses, é só compararmos o valor de e . Nesse caso, e . Como o valor P () é menor que , concluímos que devemos rejeitar . Assim, a afirmação está correta.
E pronto! Acabamos! Simples, né?
Resposta
e .
é rejeitada. A afirmação é apropriada, logo seria justo que mulheres na faixa 16-24 pagassem prêmios de seguro menores, já que dirigem menos.