Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.6 - Ex. 28
O número de chegadas de clientes a um banco foi anotado minuto a minuto para uma amostra de 70 períodos (de um minuto). Os dados foram os seguintes:
O modelo de Poisson foi proposto para modelar essas chegadas, qual a sua opinião?
Passo 1
Mais uma vez, nessa questão temos de realizar o que chamamos de “Teste de aderência”, nada mais é do que uma artimanha para ver se os valores coletadas estão de acordo com um determinado modelo.
Beleza, antes de seguir, vamos definir quem é a variável que estamos estudando:
A partir disso, queremos testar:
O teste será feito aproximado por uma distribuição , da seguinte forma:
Onde representa a quantidade de categorias, no nosso caso categorias. E é a frequência observada para cada categoria.
Já o é a frequência ESPERADA para cada categoria se essa variável realmente tivesse a distribuição sugerida; ou seja, temos de encontrar esse valor.
Mas o enunciado não nos deu um valor para , teremos de encontrar, sabendo que ele representa a quantidade média de pessoas que esperamos ver no banco em cada minuto:
Passo 2
Agora sim conseguimos encontrar as frequências que esperamos obter a partir do modelo de Poisson, lembrando que a função de probabilidade é dada por:
Vamos achar o seguinte:
E assim por diante até:
Repare que:
Já encontramos todas, basta então somar e pegar o resto:
Então:
Coloquei na tabela abaixo todas as frequencias esperadas pra você conferir:
Bateu tudo aí? Show dybola, agora tem dois pontos muito importantes... Pay attention agora!!
- Toma cuidado com as aproximações, isso porque a soma das frequencias esperadas (aquelas que você acabou de calcular) tem que ser igual a 70 (soma das frequencias que já estavam na tabela).
- Uma outra regrinha muito doida, a gente simplesmente não pode ter frequencias esperadas menores do que 5...
Eu sei... mas calma, quando encontrar frequencias menores do que 5, tudo que precisamos fazer é “fundir” as categorias. Olha só na tabela a abaixo o que muda:
Passo 3
Percebeu? Juntamos as três categorias que tinham frequencia ESPERADA menor do que 5. É só isso.
Obs: fizemos isso somente porque as frequencias esperadas tinham valores menores do que 5; não fazemos isso olhando para as frequencias observadas. Mas claro que, uma vez tendo que fazer a fusão das categorias, devemos somar também as frequencias observadas.
Para terminar o teste, temos que definir uma região crítica, como o enunciado não deu nenhum nível de significância, vamos tomar ; é o padrão.
Portanto a região crítica será do tipo:
Devemos buscar na tabela de distribuição qui-quadrado, um valor tal que:
Para achar o queridinho, vamos na coluna de 5% e na linha de graus de liberdade.
Pêra, por que? Lembra que eu falei no passo 1 que os graus de liberdade eram definidos por onde era o número de categorias?
Então, no começo da brincadeira tínhamos 8 categorias, só que precisamos fazer uma fusão lembra? Com isso ficamos com 6 categorias.
Tá então por que não temos graus de liberdade???
Não vamos ter isso porque tivemos que estimar um parâmetro; se você lembrar o enunciado não deu o parâmetro pra gente, tivemos que tirar do c*.
E toda vez que temos que estimar algum parâmetro, a gente tem que tirar mais um grau de liberdade; por isso iremos buscar na linha de
Infelizmente não!! Confuso demais né?? Mas vamo logo na tabela pra acabar essa tortura:
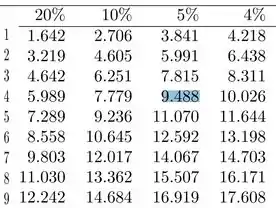
Então encontramos, ; portanto nossa RC fica assim:
Por último, podemos finalmente utilizar a qui-quadrado:
E como encontramos ele não pertence à região crítica; então devemos aceitar
Resposta
Depois de tudo isso, concluímos que sim, o modelo de Poisson pode ser usado para estudar a chegada de pessoas no banco.