Teste de Hipóteses para Proporções
Teoria
Se você chegou até aqui, é porque tá ficando expert em teste de hipóteses!
Bom, vamos lá. Antes de tudo, é importante que você saiba que aqui nosso parâmetro vai mudar totalmente dos casos anteriores.
Vamos querer fazer um teste de hipóteses para proporções . Esqueceu quem é esse carinha?
Vamos supor que numa população de 10000 pessoas, 7500 pessoas tenham o cabelo castanho. Qual vai ser a nossa proporção populacional de pessoas com cabelo castanho? Só dividir o número de elementos com as características que queremos pelo tamanho da população:
E da mesma forma que a gente tem uma proporção populacional, também vamos ter uma proporção amostral, que chamaremos de .
Agora que você já sabe disso, vamos cair dentro desse tópico! Vamos aprender a resolver esse tipo de teste de hipóteses com um exemplo.
“Segundo uma revista, as condições de mortalidade de uma região são tais que a proporção de nascidos que sobrevivem até 60 anos é de 60%. Teste essa hipótese ao nível de significância , se em uma amostra de nascimentos, verificou-se sobreviventes até anos.”
1º Passo) O primeiro passo vai ser sempre começar vendo quem é nosso parâmetro.
Lendo bem o enunciado, a gente já descobre que ele tá falando sobre proporção, ou seja, nosso amigo .
Depois disso, vamos escrever quais são nossas hipóteses:
O cara falou que a proporção de pessoas que sobrevivem até os 60 anos é de , então nossa hipótese nula vai conter essa igualdade.
Como a hipótese alternativa precisa contrariar , e o enunciado não falou nada sobre essa proporção ser menor ou maior que isso, vamos considerar que a proporção é diferente de .
Estamos em um teste de hipótese bilateral!
2º Passo) Calcular nossa estatística de teste.
Essa velha amiga você já conhece também, é ela que usamos pra tomar nossa decisão.
Como estamos em um caso de proporção, a gente pode considerar que estamos num caso de distribuição normal. Isso acontece lááá pela propriedade de aproximar a Binomial pela Normal.
Ufa! Distribuição normal de novo, então não deve mudar muita coisa do caso da média com conhecido, certo?! Quase isso, meu amigo. Vem comigo.
A fórmula pra calcular a estatística de teste no caso de um teste de hipótese para proporção vai ser:
Epa, peraí! Quem é esse mesmo?
Ele é a nossa proporção amostral! Temos que olhar pra nossa amostra, e ver a proporção de sobreviventes.
Agora vamos substituir os valores na nossa fórmula?
Guarda esse valor, ele é precioso! E claro, vem comigo pro próximo passo.
3º Passo) Agora precisamos descobrir qual é nossa região crítica, a região onde rejeitamos .
Por estarmos no caso da distribuição normal, aqui o passo a passo vai ser igualzinho ao teste de hipótese pra média com conhecido!
Como estamos num teste bilateral, nossos pontos críticos são:
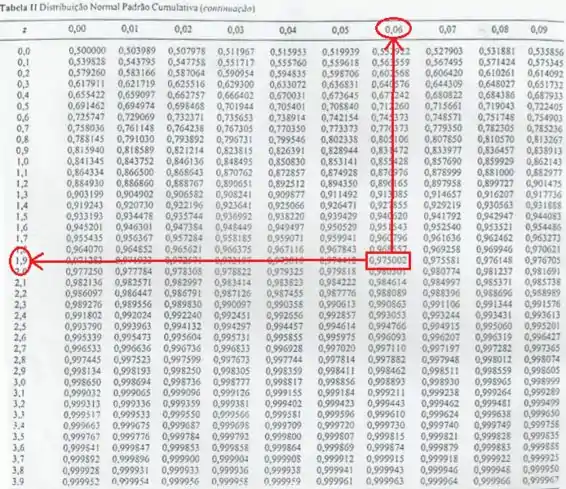
Vamos ver como isso fica no nosso desenho? Lembrando que estamos num caso da distribuição normal, então podemos trabalhar com a nossa querida curvinha.
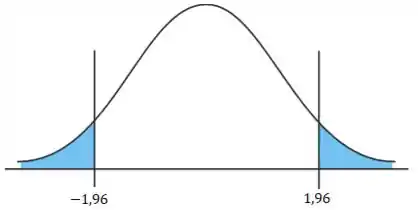
Essa dica é bem valiosa, hein: sempre faça o desenho!
4º Passo) Olhar onde o valor da estatística de teste está no desenho.
Cara, aqui vamos ver se nosso está dentro ou fora da região crítica.
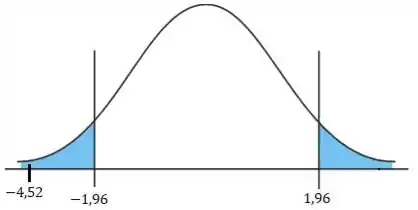
Opa! Nossa estatística de teste está dentro da região crítica. E a região crítica é onde rejeitamos !
5º Passo) Tomar a decisão
Cara, como nosso valor de caiu dentro da região crítica, rejeitamos nossa hipótese nula ! Ou seja, a proporção de sobreviventes é realmente diferente de .
Tranquilão, né?! Vem pros exercícios!
Exercícios Resolvidos
Exercício Resolvido #1
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 384.
As especificações dos pentes de memória RAM para computadores fabricados pela Companhia Boa Memória indicam que a porcentagem de pentes defeituosos não excede 5%. Uma amostra de cem desses pentes apresentou sete defeituosos.
Com base nesse resultado, podemos afirmar que as especificações estão incorretas?
- Qual a decisão a ser tomada, ao nível de significância de 0,01?
Passo 1
(a)
Primeiros definimos as hipóteses:
Com isso já temos como dados:
E também que:
Passo 2
Podemos notar que nossas hipóteses estão no caso2, por isso sua rejeição acontece em:
Vamos calcular o que falta então:
Pra isso, só usei a tabela da Normal.
Com isso:
Se isso acontecer, rejeita-se .
Passo 3
Basta então calcularmos a proporção amostral, :
Como , então estamos na região de aceitação.
Com isso não é possível rejeitar .
Resposta
Exercício Resolvido #2
Morettin & Bussab, Estatística Básica 5ª edição, pág 337
Um fabricante garante que dos equipamentos que fornece a uma fábrica estão de acordo com as especificações exigidas. O exame de uma amostra de 200 peças desse equipamento revelou 25 defeituosas. Teste a afirmativa do fabricante, nos níveis de e .
Passo 1
A proporção amostral observada de peças defeituosas foi:
Então a proporção de peças sem defeitos é:
Essa é a proporção que vamos usar no nosso teste, já que ele é sobre as peças sem defeito.
Montando as hipóteses:
Repara que aqui montamos para a hipótese nula, a afirmação do fabricante não está correta e para a hipótese alternativa a afirmação de que o fabricante está certo. Afinal, estamos aqui testando a afirmativa do fabricante.
Estamos então num teste unilateral superior.
Passo 2
A estatística de teste é dada por:
E o ponto crítico para esse tipo de teste é:
Primeiramente, vamos testar para , então:
Como a estatística deu e estamos num teste unilateral superior, o vai estar fora da região crítica! Porque a nossa aqui vai ser tudo que é MAIOR que . Então não rejeitamos a hipótese nula. Ou seja, para esse nível de significância, o fabricante não está correto, que foi a nossa hipótese .
Passo 3
Agora para vamos testar para , então:
Como a estatística deu e estamos num teste unilateral superior, o também vai estar fora da região crítica! Porque a nossa aqui vai ser tudo que é MAIOR que . Então não rejeitamos a hipótese nula. Para esse nível de significância, o nosso fabricante também não está correto.
Resposta
Exercício Resolvido #3
Elaboração Própria
A proporção de pacientes de câncer curados após 5 anos de tratamento é, segundo a literatura, de 50%. Um pesquisador deseja investigar se esta taxa é verdadeira para um determinado hospital. Para isso, ele usa uma amostra de 200 pacientes com câncer, e observa que 92 deles foram curados após 5 anos de tratamento. Teste se o dado da literatura é otimista a um nível de significância de 5%.
Passo 1
Organizando nossos dados:
Considerando as hipóteses:
Por que menor que na alternativa? Porque queremos verificar se essa dado da literatura não tá mais alto do que a realidade!
Passo 2
Calculando nossa estatística de teste:
Passo 3
Agora calculamos nossa região crítica. Para o teste unilateral inferior o ponto crítico é dado por:
Procurando esse na tabela temos que...
Como estamos no teste unilateral inferior, a região crítica vai ser tudo que for MENOR que esse . Nossa estatística de teste é maior que isso, certo?
Então não caímos na RC, ou seja, não rejeitamos a hipótese nula!
Resposta
Não rejeita-se .
Exercício Resolvido #4
Sisne – Estatística II, Slides Prof. Antônio Roque, Aula 12.
Estamos interessados em saber que proporção de motoristas da população usa cinto de segurança regularmente. Em uma pesquisa com 300 motoristas, 123 deles disseram que usam regularmente o cinto de segurança. Podemos concluir desses dados que a proporção de motoristas que usa cinto de segurança é inferior a 50%? Teste a um nível de significância de 10%.
Passo 1
Organizando nossos dados:
Considerando as hipóteses:
Por que menor que na alternativa? Porque queremos verificar se a proporção é inferior!
Passo 2
Calculando nossa estatística de teste:
Passo 3
Agora calculamos nossa região crítica. Para o teste unilateral inferior o ponto crítico é dado por:
Procurando esse na tabela temos que...
Como estamos no teste unilateral inferior, a região crítica vai ser tudo que for MENOR que esse . Nossa estatística de teste é menor que isso, certo?
Então caímos na RC, ou seja, rejeitamos a hipótese nula!
Resposta
Rejeita-se .
Exercício Resolvido #5
Elaboração Própria
Sabe-se que a proporção de estudantes de ensino superior de instituições públicas que compram livros relativos ao seu curso é de 13%. O Reitor de uma instituição federal afirma que em sua instituição essa proporção é maior. Para testar sua hipótese, seleciona uma amostra de 600 estudantes de sua instituição, destes, 70 responderam que compram livros relativos ao seu curso. Teste as hipóteses ao nível de significância de 0,05, e conclua sobre a afirmação do Reitor.
Passo 1
Organizando nossos dados:
Considerando as hipóteses:
Por que maior que na alternativa? Porque queremos verificar se a proporção é maior, como o reitor afirmou!
Passo 2
Calculando nossa estatística de teste:
Passo 3
Agora calculamos nossa região crítica. Para o teste unilateral superior o ponto crítico é dado por:
Procurando esse na tabela temos que...
Como estamos no teste unilateral superior, a região crítica vai ser tudo que for MAIOR que esse . Nossa estatística de teste é menor que isso, certo?
Então não caímos na RC, ou seja, não rejeitamos a hipótese nula! Logo, não podemos afirmar que o reitor estava certo!
Resposta
Não rejeita-se . Não podemos afirmar que o reitor estava certo.