Teste de Hipóteses para Variância Populacional
Produzido por Jorge Alberto NascimentoTeoria
Opa, mais um teste para nossa lista?! Que beleza!

Não precisa se desesperar não! Aguenta firme que já tá acabando.
Vamos começar a ver esse negócio com um exemplo:
“Um órgão de defesa do consumidor teste regularmente o peso dos produtos vendidos em estabelecimentos comerciais. Uma empresa alega que seus produtos apresentam no máximo uma variância de . A inspeção de uma amostra aleatória de produtos dessa empresa acusou uma variância amostral de . Considerando que os pesos desses produtos seguem uma distribuição Normal, teste a alegação da empresa a um nível de significância de .”
1º Passo)
Vamos primeiro fazer o que já sabemos, que é definir as hipóteses. Aqui estamos testando a variância populacional, então nossas hipóteses vão envolver . A empresa alega que a variância não passa de , então vamos igualá-la a isso aí na hipótese nula:
E como queremos testar a alegação da empresa, na hipótese alternativa vamos dizer o contrário do que a empresa diz. Se foi dito que a variância não passa de , vamos dizer que ela na verdade passa disso sim, ou seja, é maior que :
Estamos num teste unilateral superior!
2º Passo)
Agora vamos calcular nossa estatística de teste, que agora não é mais dada pela estatística da Normal, e sim pela estatística da distribuição Qui-Quadrado. Ela é dada por:
Onde é o tamanho da amostra, é a variância amostral e é o valor teórico da nossa variância até então (em outras palavras, é o valor que usamos na construção das hipóteses). Então substituindo na equação os valores do nosso exemplo:
3º Passo)
Agora temos que calcular nossa região crítica e ver se nossa estatística de teste está dentro dela para tomar uma decisão, como sempre fizemos.
Porééém, agora nossa região crítica também é um pouquinho diferente, já que usamos a distribuição . Nosso gráfico vai ser algo desse tipo:
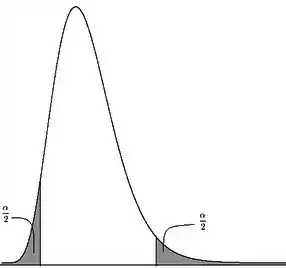
A curva agora não é simétrica, pois é a curva da Qui-Quadrado! Precisamos então descobrir como achar o ponto crítico que divide o gráfico entre região de aceitação e região crítica. Vamos ver como que fica issaê para cada tipo de teste.
Teste unilateral superior:
Onde é o nível de significância e é o grau de liberdade.
Temos que procurar na tabela Qui-Quadrado, ao nível de significância pedido no teste e com graus de liberdade como parâmetros, onde:
Igual a T de Student! No nosso exemplo então, queremos:
Procurando na tabela Qui-Quadrado...
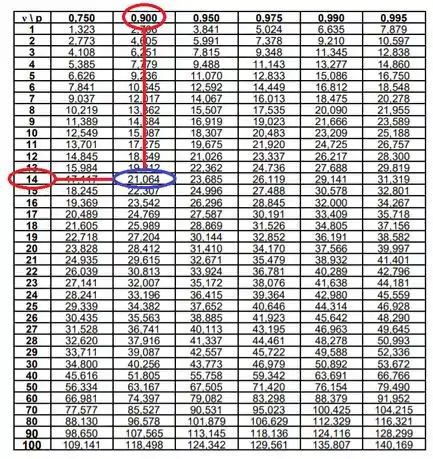
“Uééé, mas por que você circulou o ? O parâmetro não era o nível de significância ?”
Sim, o nível de significância é esse mesmo! Mas o parâmetro que você vai procurar depende da tabela que tá usando. Nessa aí da imagem, repara que o parâmetro na primeira linha é um , não . Quando nossa tabela tiver em função de , nós sempre procuramos o complementar do nível de significância:
Ou seja, nosso nível de confiança! Você tem que descobrir qual tipo de tabela sua universidade/professor(a) usa, e aí:
- Se for em função de , você procura a complementar do .
- Se em função de , você procura o direto mesmo.
Então nossa região crítica:
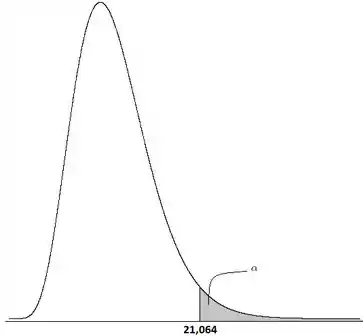
É tudo que é MAIOR que nosso ponto crítico, pois estamos num teste unilateral SUPERIOR. E lembrando que nossa estatística de teste vale ...
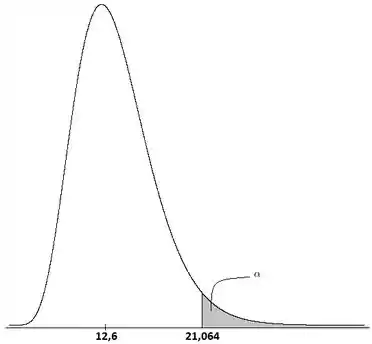
Vemos que ela cai fora da região crítica. Ou seja, não rejeitamos a hipótese nula, então a variância do peso dos produtos realmente pode ser !
Vamos terminar de ver como são os pontos críticos e região crítica para os outros tipos de teste.
Teste unilateral inferior
O ponto crítico vai ser dado por:
Bem parecido com o caso unilateral superior, porém agora nosso parâmetro é o ao invés de . Mas esse é o valore que deve ser procurado diretamente na tabela caso sua tabela esteja em função de , não pode esquecer! Se ela estiver em função de , você procura pelo complementar desse valor.
A região crítica fica sendo tudo que é MENOR que o ponto crítico, já que estamos num teste unilateral INFERIOR:
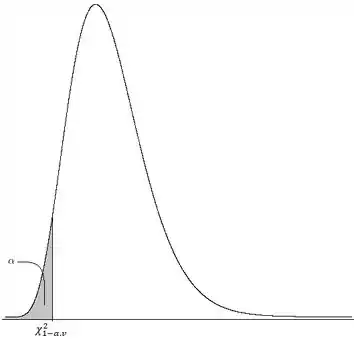
Teste Bilateral
Nesse caso, temos dois pontos críticos:
A diferença aqui é que nós estamos dividindo o nível de significância por dois, já que vamos ter duas áreas de rejeição. Nossa região crítica fica assim no final:
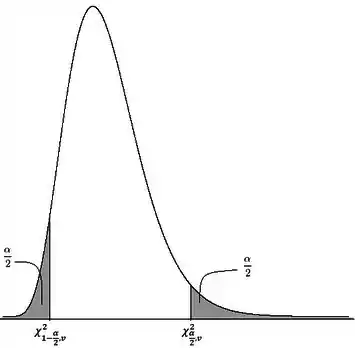
IMPORTANTE: Não podemos esquecer que a variância é o desvio padrão ao quadrado! Então com o passo-a-passo deste tópico também poderíamos ter resolvido um teste de hipótese para desvio padrão populacional. Basta lembrar de elevar o valor dele ao quadrado e resolvemos o teste como se fosse para a variância. Vamos resolver isso direitinho nos exercícios! =)
2º Passo)
3º Passo)
IMPORTANTE: Não podemos esquecer que a variância é o desvio padrão ao quadrado! Então com o passo-a-passo deste tópico também poderíamos ter resolvido um teste de hipótese para desvio padrão populacional. Basta lembrar de elevar o valor dele ao quadrado e resolvemos o teste como se fosse para a variância. Vamos resolver isso direitinho nos exercícios! =)
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Uma máquina de preenchimento automático é utilizada para encher garrafas com detergente líquido. Uma amostra aleatória de garrafas resulta em uma variância da amostra do volume de enchimento de onça fluida. Se a variância do volume de enchimento exceder onça fluida, existirá uma proporção inaceitável de garrafas cujo enchimento não foi completo ou foi em demasia. Há evidência nos dados da amostra sugerindo que o fabricante tenha um problema com garrafas com falta ou excesso de detergente? Use e considere que o volume de enchimentos tem distribuição normal.
Passo 1
Queremos testar o valor de uma variância populacional! Começamos seeempre definindo as hipóteses:
Pois queremos testar se o fabricante vai ter problema no enchimento das garrafas.
Se essa variância for maior do que , isso indicará que as garrafas podem estar com falta ou excesso de detergente, isso é, não estão próximas ao valor esperado.
Pelas hipóteses criadas, estamos num teste unilateral superior!
Passo 2
Vamos calcular primeiramente nossa estatística de teste para teste de hipótese da variância:
Passo 3
Agora calculamos nossa região crítica. Como o nível de significância é de , nosso ponto crítico vai ser dados por:
E vamos ter graus de liberdade, então podemos procurar na tabela Qui Quadrado e achar o valor desse cara:
Opa! Então nossa estatística de teste é menor que o ponto crítico. Isso significa que a estatística de teste caiu fora da região crítica, pois num teste unilateral SUPERIOR a RC é tudo que for MAIOR que o ponto crítico.
E se caiu fora da RC, não podemos rejeitar a hipótese nula!
Resposta
Não rejeita-se .
Exercício Resolvido #2
Prof.ª Lilian M. Lima Cunha – Estatística Aplicada II - USP
Numa determinada empresa, empregados que desempenham a mesma função têm salarios diferentes em função do tempo de casa e bonificações por desempenho. Segundo a empresa, o desvio-padrão para o salario de uma certa função é de . Entrevistando funcionários que desempenham essa mesma função, verificou-se que seus salários eram, respectivamente, .
Testar a afirmação da empresa com significância de 5%, supondo que os salários sejam normalmente distribuídos.
Passo 1
Queremos testar o valor de um desvio padrão populacional! Para isso, basta lembrarmos que o desvio padrão é a raiz quadrada da variância. Então se elevarmos os valores de desvio padrão ao quadrado, podemos realizar esse teste normalmente como fazemos para a variância.
Então agora definimos as hipóteses:
Pois queremos testar se o desvio padrão é igual ao valor relatado pela empresa ou não.
Então estamos num teste bilateral!
Passo 2
Para continuar nossa questão, precisamos do valor da variância amostral . E para calculá-la, precisamos do valor da média amostral. Então vamos lá:
E daí calculamos a variância amostral:
Agora podemos calcular nossa estatística de teste para teste de hipótese da variância:
Passo 3
Agora calculamos nossa região crítica. Como o nível de significância é de , nossos pontos críticos vão ser dados por:
E vamos ter graus de liberdade, então podemos procurar na tabela Qui Quadrado e achar o valor desses caras:
E no teste bilateral nossa região de aceitação é tudo que está entre esses dois pontos, ou seja, nossa região crítica é tudo que for menor que e tudo que for maior que .
Como nossa estatística de teste deu , ela cai fora da região crítica e dentro da região de aceitação!
E se caiu fora da RC, não podemos rejeitar a hipótese nula!
Resposta
Não rejeita-se .
Exercício Resolvido #3
Prof.ª Lilian M. Lima Cunha – Estatística Aplicada II - USP
Uma caixa de fósforos de certa marca vem com a inscrição: “contém, em média, palitos”. Segundo o fabricante, o desvio-padrão é de, no máximo, dois palitos. Em uma amostra com caixas, entretanto, foi encontrado um desvio-padrão amostral de palitos. Supondo que o número de palitos por caixa seja uma variável normal, teste a afirmativa do fabricante utilizando um nível de significância de 1%.
Passo 1
Queremos testar o valor de um desvio padrão populacional! Para isso, basta lembrarmos que o desvio padrão é a raiz quadrada da variância. Então se elevarmos os valores de desvio padrão ao quadrado, podemos realizar esse teste normalmente como fazemos para a variância.
Então agora definimos as hipóteses:
Pois queremos testar se o desvio padrão está dentro do que a empresa relatou, ou seja, se ele não passa de dois. Para isso, vamos testar se ele é de fato maior que , o que em função da variância seria .
Então estamos num teste unilateral superior!
Passo 2
Podemos começar calculando nossa estatística de teste para teste de hipótese da variância:
Passo 3
Agora calculamos nossa região crítica. Como o nível de significância é de , nosso ponto crítico vai ser dados por:
E vamos ter graus de liberdade, então podemos procurar na tabela Qui Quadrado e achar o valor desse cara:
E no teste unilateral superior nossa região crítica é tudo que for MAIOR que o ponto crítico, ou seja, maior que . Como a estatística de teste deu ela cai dentro da RC, o que significa que rejeitamos a hipótese nula!
Resposta
Rejeita-se .
Exercício Resolvido #4
Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Um fabricante de baterias para automóveis afirma que a duração de suas baterias é em média de anos, as quais tem uma distribuição normal com um desvio padrão igual a anos.
- Um auditor pega uma amostra aleatória de de tais baterias e obteve um desvio padrão de anos. Deseja-se saber se existe diferença do desvio padrão ao nível de significância de ?
Defina claramente sua hipótese. Mostre o resultado através do cálculo da estatística do teste. Esboce um gráfico da distribuição do teste indicando claramente a área de rejeitação e aceitação de .
Passo 1
a)
Aqui queremos fazer um teste de hipótese para a variância, temos o valor do desvio padrão e . Calculando as variâncias equivalentes:
. Nossa hipótese nula vai concordar com a afirmação de que a variância é igual ao valor populacional:
E queremos verificar se esse valor na verdade é diferente, então nossa hipótese alternativa tem que testar isso:
Estamos num teste bilateral.
Passo 2
Em um teste de hipótese para variância, usamos a distribuição Qui Quadrado para tomar decisões.
Vamos calcular primeiramente nossa estatística de teste para teste de hipótese da variância:
Como (pois temos baterias na nossa amostra):
Passo 3
Agora calculamos nossa região crítica. Como o nível de significância é de , nossos pontos críticos vão ser dados por:
E vamos ter graus de liberdade, então podemos procurar nossos pontos na tabela Qui Quadrado e achar os pontos críticos:
Passo 4
Com esses pontos críticos e com a nossa estatística de teste, podemos observar pelo gráfico que ela cai fora da região crítica:
O que significa que nós não rejeitamos a hipótese nula!
Resposta
Não rejeita-se a hipótese nula.
Exercício Resolvido #5
Um fabricante de relógios deseja conhecer a variabilidade do seu produto. Para isso registrou os desvios em segundos de 24 relógios, relativamente a um relógio de alta precisão ocorridos ao fim de um mês e obteve como resultado: média de 0,8 segundos e desvio padrão de 1,5 segundo.
Pede-se:
- Com base na longa experiência com os relógios desta marca o fabricante acredita que o verdadeiro desvio padrão é no máximo 1,2 segundos. Ao nível de significância de 1% e 5% podemos afirmar que o fabricante está correto?
Mostre claramente o seu desenvolvimento para o teste de hipótese determinando: as hipóteses nula e alternativa, a estatística do teste e a decisão acompanhada de um gráfico da função de probabilidade da estatística do teste, indicando claramente as áreas de rejeição e de aceitação de .
Passo 1
a)
As informações da nossa amostra são:
E nossa amostra tem 24 relógios, então:
Passo 2
Queremos testar o desvio padrão ser no máximo 1,2 segundos, então:
Sinal de igualdade sempre! Como é no máximo 1,2 segundos, qualquer valor menor que 1,2 segundos ainda conta. Então nossa alternativa tem que ser o contrário disso, ou seja, tem que ser maior que 1,2 segundos:
Passo 3
Teste de hipótese para desvio padrão a gente vai usar a distribuição qui-quadrado!
Vamos começar pelo nível de significância de 1%, ou seja:
Na curva da qui-quadrado, teríamos isso aqui:
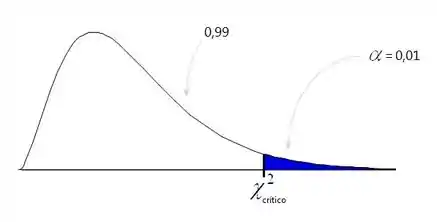
na ponta direita porque nossa hipótese alternativa tem o sinal de maior que! E como a área abaixo da curva tem que ser 1, achamos a área em branco fazendo .
Lembrando que a região de rejeição está em azul e a de aceitação está em branco!
Passo 4
Para 1% de significância, nosso vai ser:
Já que temos à direita da curva, separando a região crítica da região de aceitação.
E como temos uma amostra de 24, nosso grau de liberdade será:
Procurando esse qui-quadrado na tabela, temos:
E para 5% de significância, nosso vai ser:
Passo 5
A nossa estatística de teste vai ser:
Substituindo os valores que temos (lembrando que a variância é o valor que estamos testando):
Passo 6
Para 1% de significância, temos que ver se ela tá na área azul ou branca do gráfico:
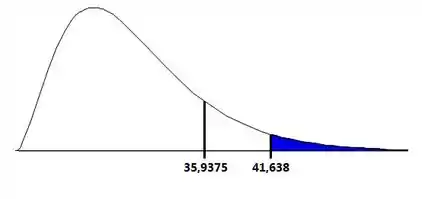
Branca! Então não rejeitamos a hipótese nula.
Passo 7
E para 5% de significância, nossa região crítica fica:
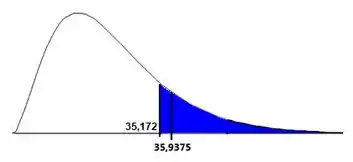
Estatísitca de teste DENTRO da área azul. O que significa que rejeitamos a hipótese nula!