Teoria
Função type()
Fala aí, cara! Beleza? Você provavelmente já usou vários números em Python pra fazer algumas contas, mas hoje eu vou te contar algumas coisas que acontecem por baixo dos panos quando utilizamos números em Python.

Mas calma, antes de começar nossa jornada pokemón, deixa eu te apresentar um comando que vai ajudar a gente no estudo dos tipos de dados: type().
Esse comando retorna o tipo do dado que você colocar dentro dos parênteses. Olha só um exemplo do funcionamento dele:
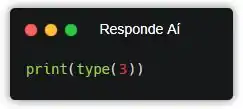
Ao executar esse programa, será exibido o tipo da informação que a gente colocou dentro da função type(). A primeira coisa que eu quero te falar sobre esses códigos é sobre a gente ter colocado uma função dentro da outra. Basicamente, a gente tá pegando o resultado de uma e colocando na outra direto, beleza? A primeira ordem ali no, nosso idioma, ficaria assim: “exiba o resultado do tipo do valor 3”.

Depois de executar esse código, o resultado é esse:
![]()
O primeiro retorno é int, que é uma abreviação pra integer, ou seja, número inteiro em inglês. Show! Até aqui, tá tudo lindo. Esse valor tem todas as características que a gente conhece sobre números inteiros, lá da matemática.

No entanto, não há nada de muito especial neles, e a gente consegue usar números inteiros sem se preocupar muito. Você só precisa se lembrar que o nome do tipo de dados inteiros é “int”, minúsculo. Mas, e se em vez de inteiros, a gente quiser números reais (com vírgula)?

Vamos ver agora!
Números float em Python
Cara, se você editar um pouquinho o código que a gente escreveu ali em cima e colocar um número com um ponto dentro, tipo assim:
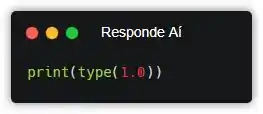
Depois de executar:
![]()
O nome é float... Será que o 1.0 voa?! Bom, os números reais são chamados de ponto flutuante em programação, e em inglês é float, okay?! Mas cara, talvez você esteja se perguntando o porquê de 1.0, que é um número inteiro, retornou float. A resposta é que, simplesmente, Python olhou, viu um ponto “.” ali no meio, e chutou que é float, na cara de pau. Então lembre-se, sempre que você tiver um número com “.”, vai ser um float, sempre.

Os números do tipo float são mais abrangentes que os números inteiros. Essas paradas de conjuntos numéricos, reais e inteiros, são matéria antiga. Talvez você não lembre bem do ensino fundamental (muito tempo atrás). Mas eu pesquisei aqui e vou te lembrar. Olha aqui embaixo:
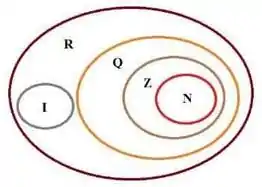
Nessa imagem, os números inteiros (Z) estão dentro dos números reais (R). Ou seja, os números inteiros podem ser representados como reais, mas os reais não podem ser representados como inteiros. Porém, a linguagem Python faz o favor de verificar os tipos pra gente, então a gente não tem que lidar com isso.

Eu só queria enfatizar que, sempre que houver alguma expressão envolvendo números não inteiros, o resultado vai ser um número real. Olha esse código:

A gente sabe que se a gente somar 1.5 com 2.5 na nossa calculadora, o resultado vai ser 4, um número inteiro. Porém, como a gente usou números reais na nossa expressão, tudo vai ser automaticamente convertido pra real. Olha o resultado:
![]()
Viu? O resultado da soma é 4, mas foi exibido 4.0 quando a gente mandou imprimir. Além disso, o comando type() aplicado na variável c retornou pra gente o tipo float, o que confirma que o resultado da nossa expressão é considerado um valor real, e não inteiro.

Um caso especial onde a gente tem que ficar ligado é em expressões de divisão. Olha:

Ao executar esse programa, a gente obtém:
![]()
Percebe que o resultado é 2.0? Isso é porque a gente usou o operador de divisão real (/). Se a gente tivesse usado o operador de divisão inteira (//), o resultado seria 2, um número inteiro arredondando pra baixo, caso a divisão tenha resto. Ou seja, 5//2 também resulta em 2.

Interpretação de números reais
Agora, pra finalizar, eu queria te falar sobre os problemas dos números reais no computador. Cara, lembra que eu te disse que os computadores só entendem linguagem de máquina, composta por zeros e uns??! Então... Como o computador pode armazenar um número inteiro, como por exemplo o número 25, se ele só entende zeros e uns??

Vou te contar! Todos os números inteiros podem ser representados por combinações entre zeros e uns. Ou seja, números binários. Você não precisa se aprofundar nisso agora, eu só tô citando isso pra você perceber que armazenar números reais com combinações de zeros e uns é algo bastante problemático. Olha, resolve essa conta aqui, de cabeça:
![]()
Parece de boas, né? O resultado é 0.6. Agora faz essa:
![]()
Bom, o resultado é 0.6 também, né? Independentemente da ordem. Mas cara, se a gente fizer essas duas contas em Python, se liga no que acontece:
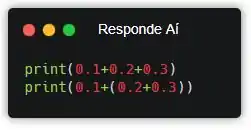
![]()
Viu? Por algum motivo, os resultados foram diferentes. E esse motivo é bem complicado, mas o que é importante pra você saber por enquanto é que os números float na computação são aproximações muito boas, mas nunca são exatos.

No caso da linguagem Python, que a gente tá usando, a precisão vai ser sempre de aproximadamente 16 casas decimais (também chamado de “precisão dupla”). Isso significa que as 16 primeiras casas decimais de um número real vão estar sempre certas, porém, depois disso o valor é duvidoso. Um exemplo é aquele 1 ali no fim. Repara que ele é exatamente o 16º dígito decimal. A partir desse dígito, incluindo ele, os demais não são confiáveis, beleza?!

Tô te contando isso porque é muito comum a gente ter bugs no nosso programa por conta das imprecisões do tipo float. Então, se algo estiver dando errado na hora que você estiver tentando fazer algum exercício, mantenha a calma e dá uma olhada nos números float.

Ah... O primeiro caso ali, que retornou 0.6, por acaso foi arredondado de forma certeira na hora de exibir. Mas isso não significa que ele é exato. Se a gente fosse olhar os dígitos depois da 16ª casa decimal, com certeza também teria imprecisão, ok?!
Por hoje é isso, galera! Valeu, maninho!

Números float em Python
Interpretação de números reais
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Escreva um programa que recebe um número inteiro do usuário e exibe o dígito das dezenas. Verifique o funcionamento do seu programa com os seguintes dados:
1935, tem que retornar 3.
3099, tem que retornar 9.
4, tem que retornar 0.
Passo 1
Pra resolver esse exercício a gente vai precisar lembrar dos operadores matemáticos em Python. Mas primeiro, vamos escrever o código que recebe o número inteiro.
Pra perguntar algo pro usuário, a gente sempre usa a função input().
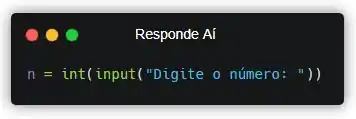
Se liga que a gente precisa colocar o comando input() dentro do int() nesse caso. Isso é porque a função input() sempre retorna um valor no formato de texto! Pra gente fazer operações matemáticas, precisamos converter esse valor pra um tipo numérico. Nesse caso, vamos converter pra inteiro, porque tá escrito no enunciado que é pra receber um número inteiro!
Agora a gente precisa pegar o dígito da casa dezenas.
Passo 2
Ok, essa parada de casa das dezenas é matéria lá do ensino fundamental e talvez você não lembre bem, mas calma! Eu te explico. A gente vai usar como exemplo o número 188, que é o número do centro de valorização da vida.
Caso você não conheça, o Centro de Valorização da Vida é um atendimento 24h que realiza apoio emocional e prevenção do suicídio. As ligações são completamente gratuitas e sigilosas. Se você estiver passando por alguma situação difícil, pode ligar pra lá, ok?! Sobre qualquer assunto!
Mas caso você esteja de boas, vamos continuar com a revisão! Olha o número:

Ou seja, o último 8 é uma unidade. O segundo 8, de trás pra frente, tá na casa das dezenas (pois é um 80). O penúltimo número, o 1, tá na casa das centenas (é um 100). Se houvesse um quarto número, de trás pra frente, este estaria na casa das unidades de milhar, etc.
Mas ok, agora que a gente já sabe que a casa das dezenas é sempre o penúltimo dígito do número, como podemos calcular ele de forma matemática? Bom, pra isso a gente vai usar a divisão por dez! Pra esse outro exemplo, pensa no número 1234. Vamos dividir ele por dez:
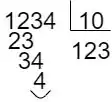
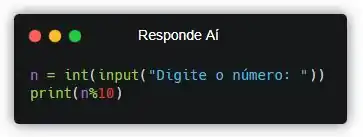
Repara que o resultado da divisão inteira desse número por 10 é igual ao número sem o último dígito (a gente deletou o último dígito quando fez a divisão inteira por 10!!). E o resto da divisão é justamente o último dígito! Lembra do operador de resto em Python?
Mas acontece que o enunciado não pede o último dígito, mas sim o penúltimo. Mas, cara! Olha de novo ali na divisão por dez. Reparou que o penúltimo dígito de 1234 é justamente o último dígito de 123?! Então vamos juntar as duas operações pra resolver nosso problema!
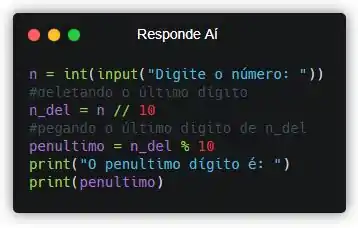
Passo 3
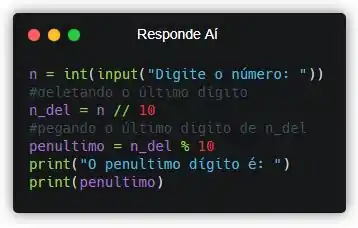
Sempre é bom a gente fazer alguns testes antes de entregar nosso exercício! Principalmente se o enunciado fornecer dados de teste. Então, vamos testar com os dados fornecidos!

![]()
![]()
Repara que todas as respostas foram iguais às previstas no enunciado. Com isso, a gente pode considerar que finalizamos o exercício!

Resposta
Exercício Resolvido #2
USP, adaptado.
Dados os números reais , e , calcular as raízes de uma equação do 2º grau na forma .
Observações:
- Caso , o programa deverá imprimir a seguinte frase: “Não há raízes reais.”.
Passo 1
Beleza, para calcularmos as raízes de uma equação do 2º grau, basta nos recordarmos da famosa fórmula de Bhaskara:
Passo 2
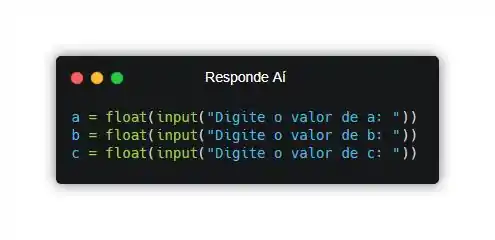
Agora que já nos familiarizamos com a parte matemática, está na hora de declararmos as variáveis que armazenarão os dados de entrada do nosso programa:
Passo 3
Com essas variáveis declaradas, podemos agora declarar a variável e inicializá-la com a expressão :
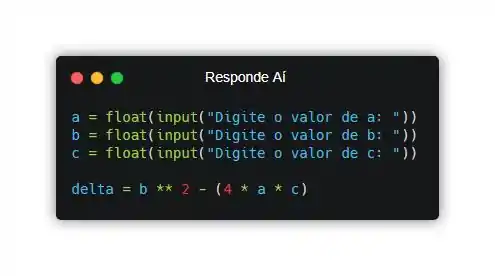
E já aproveitando que temo o valor de podemos agora mesmo cuidar da observação fornecida pelo enunciado, que é o caso em que :
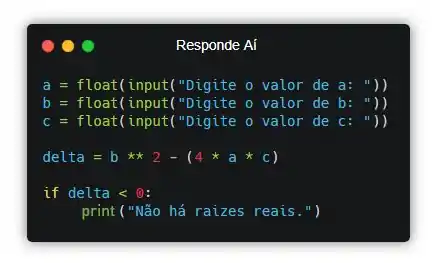
Passo 4
Continuando com o código, para evitarmos repetições, podemos declarar uma variável chamada que nos ajudará no cálculo das raízes da função:
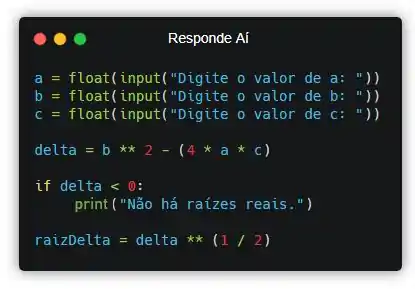
Passo 5
Até que enfim, podemos calcular o valor de que no código será representado pela variável :
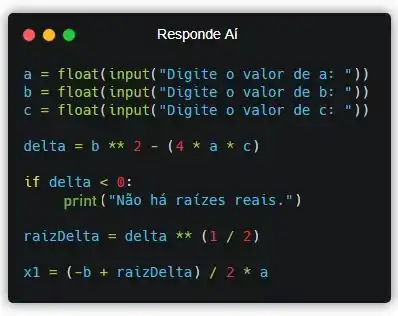
Passo 6
Porém, antes de calcularmos vamos verificar se , isso fará com que economizemos computação. Pois, se , e nós já temos o valor de .
Para isso, basta fazermos o seguinte:
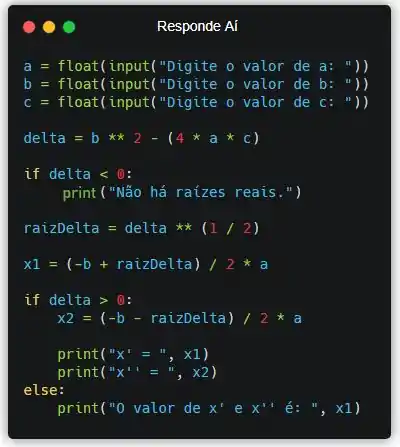
Onde, se calcularemos e realizaremos a impressão de e logo em seguida. Caso contrário, não computaremos o valor de e apenas imprimiremos o valor de afirmando que as duas raízes são iguais.
Resposta
Portanto, o código para o cálculo das raízes de uma função do 2º grau é:
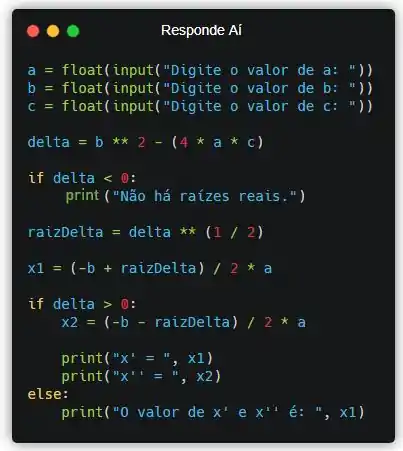
Exercício Resolvido #3
Estácio – CCT0433 (PROGRAMAÇÃO III), 2018
Um número imaginário como 3+4i pode ser representado em Python por qual dos seguintes tipos primitivos:
- tuple
- int
- float
- array
- complex
Passo 1
E aí! Vamos analisar essa questão alternativa por alternativa!
A primeira alternativa, tupla, é uma lista imutável. É um tipo de dados onde a gente consegue agrupar vários dados em comum em uma só variável, e não tem nada a ver com números imaginários ou complexos. Então bora olhar pra segunda alternativa.
Passo 2
O tipo int em Python representa números inteiros, e o número imaginário com certeza não é inteiro, então não é essa a alternativa que a gente tá procurando.
Passo 3
O tipo float em Python representa números reais. Os números reais incluem todos os inteiros e ainda incluem os números decimais, mas não incluem os complexos ainda. Então, não pode ser essa também.
Passo 4
Array, em programação, se refere a tipos de dados de agrupamento onde a gente consegue colocar vários dados em comum em uma mesma variável de uma forma mutável. O array em python tem o nome de “lista” (list, em inglês). Mas não é o que a gente quer também! ☹
Passo 5
Ok, a gente quer saber o nome do tipo de dados de um número complexo. O nome “complex” é bem sugestivo, e é a alternativa correta nessa questão! Olha como a gente pode criar dados desse tipo em Python:
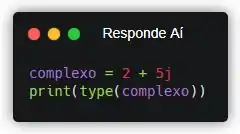
Se liga que, matemáticos usam i pra representar os números imaginários, mas engenheiros usam j. Os criadores de Python preferiram seguir a notação dos engenheiros.
Se a gente executar esse programa aí (apertando F5, caso você esteja usando o mesmo editor de código que eu), você vai ter esse resultado:
![]()
O que confirma pra gente que o nome do tipo de dados de números complexos/imaginários em Python é ‘complex’.
Resposta
Alternativa e.
Exercício Resolvido #4
UFF (Adaptado).
Faça um programa que leia três valores e imprima a área de um trapézio que tenha A e B como bases e C como altura.
Passo 1
E aí! Pra começar, a gente precisa lembrar da fórmula da área do trapézio, cara!
![]()
Aí sim! Vamos começar perguntando pro usuário os valores de A, B e C.
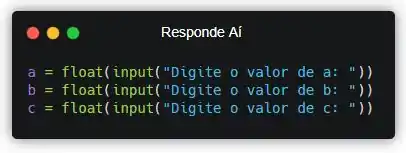
Não esqueça que a função input() sempre retorna um texto, então a gente precisa converter esse valor pra um tipo numérico pra poder fazer operações matemáticas, ok?! Nesse caso a gente vai usar float, já que medidas podem ser decimais.
Passo 2
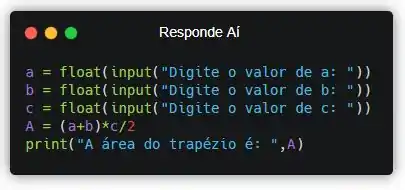
O segundo passo é aplicar a fórmula.
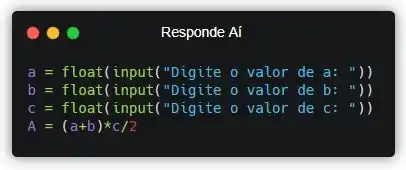
Criamos uma variável chamada A e aplicamos a fórmula. Agora só falta a gente exibir!
Passo 3
Pra exibir, a gente precisa do comando print().
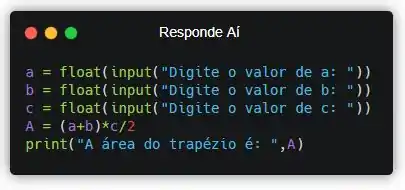
Repara que a gente consegue unir as duas informações usando uma vírgula dentro do comando print(), mas é só nesse comando mesmo. Cada função reage de uma forma às vírgulas, beleza?!
Valeuuu!
Resposta
Exercício Resolvido #5
PUC-Rio
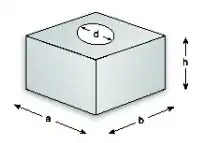
Escreva um programa para calcular a metragem necessária para forrar uma caixa com uma tampa circular, cujas dimensões são ilustradas na figura abaixo. O programa deve ler do teclado os valores das dimensões da peça.
Passo 1
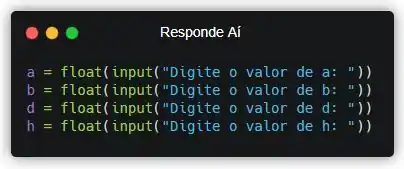
Fala aí, doido!! Vamos começar lendo os valores de a, b, h e d. Pra isso, vamos usar o comando input().
Agora a gente tem que fazer as continhas das áreas. Vamos começar calculando as áreas laterais.
Passo 2
Se liga que as áreas laterais são retângulos. Pra isso, precisamos multiplicar a base pela altura.
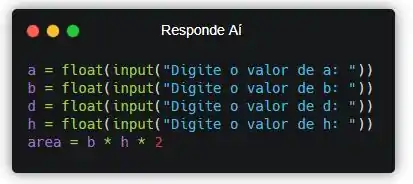
Se liga que eu multipliquei por dois. Isso porque a parte oposta da caixa vai ter a mesma área que a da frente. Agora vamos somar isso a área das outras duas faces.
Passo 3
Vamos incrementar na área que a gente já tem a área das outras duas faces do cubo.
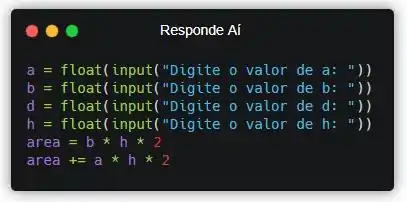
Beleza! Agora precisamos calcular as partes superior e inferior.
Passo 4
Se você reparar bem, a base e altura das partes superior e inferior são dadas por a*b. Então vamos passar isso pro código!
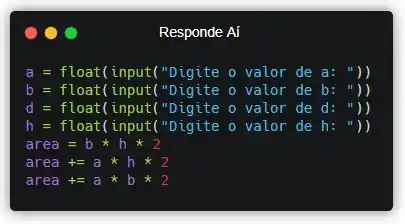
Repara que a gente sou o operador de incremento mais uma vez (+=). Esse operador soma ao valor antigo na variável “area”, guardando o somatório no final.
Agora que já calculamos toda área do cubo, precisamos desconsiderar a parte da abertura (círculo branco na imagem). Então, vamos descartar essa parte da área.
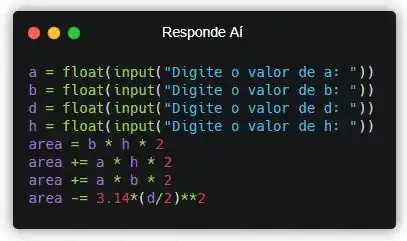
Pronto! Decrementamos do nosso somatório a área da tampa, pois não vamos precisar dela. Agora, só precisamos exibir o resultado pro usuário.
Passo 5
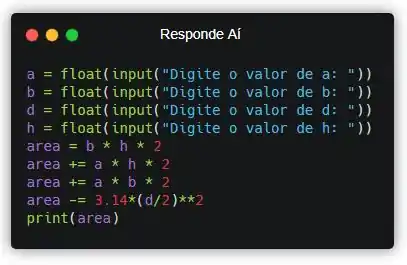
Pra exibir o resultado pro usuário, a gente precisa usar o comando print(). Vamos lá!
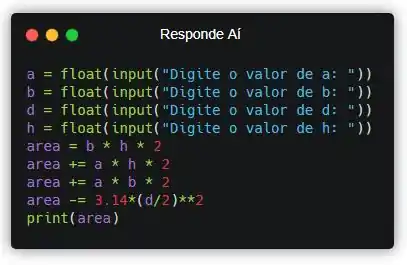
Assim, a área final vai ser mostrada pro usuário, finalizando nosso exercício!!! Valeuu
Resposta
Exercício Resolvido #6
Estácio
Considere a seguinte linha de comando:
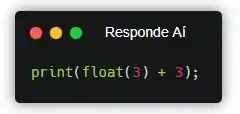
Qual é o resultado dessa expressão?
- 6
- 0
- 3.0+3
- 6.0
Passo 1
Fala aí! Cara, primeiramente, eu queria comentar com você daquele “;” ali no final da linha. O QUE É ISSO??!

O uso do “;” no final de todas as linhas é obrigatório outras linguagens de programação famosas, como C, Javascript, Pascal, etc. Não é obrigatório em Python, mas também não é proibido. Ou seja, aquele ponto e vírgula aí não tá fazendo nada! É só porque programadores experientes que já tem o hábito de pôr um “;” no final não ficarem tão desconfortáveis, beleza?!

Show! Agora vamos analisar a que vai ser exibido depois de executar nosso programa. Se liga que os números “3” ali são inteiros, mas um deles tá dentro da função float(), então vai ser transformada pra número real. No fim, teremos a soma entre um número real e um número inteiro.

Cara, geralmente não é possível fazer operações com dados de diferentes tipos, mas números reais e inteiros são uma exceção. Sempre que houver operações combinando inteiros e reais, Python vai converter tudo pra real automaticamente, beleza?! Então, nesse caso, o resultado vai ser 3+3, na notação de float.

Por isso, a resposta é 6.0, alternativa d!
Entendeu, né?! Valeuuuu!
Resposta
Alternativa d)
Exercício Resolvido #7
PUC-Rio, adaptado.
Escreva um programa que leia do teclado as duas notas de um aluno, calcule e exiba a média aritmética das notas.
Passo 1
Cara! Se a gente precisa pedir dados pro usuário, automaticamente a gente tem que lembrar da função input(), beleza?! Então vamos lá!
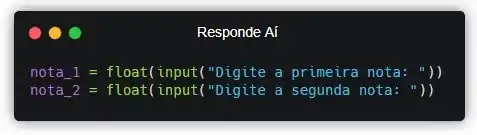
Como precisamos de duas notas, então colocamos uma nota em cada variável. Mas se liga que a gente tá convertendo pra float! O resultado da função input() é, por padrão, sempre string (texto). Pra gente converter pra número real a gente precisa colocar esse resultado dentro da função float(), ok?!

Obs: a gente usou float em vez de int porque as notas de um aluno podem ter números com vírgula.
Passo 2
Beleza! Agora que a gente tem os dois valores, a gente pode fazer a média aritmética. A média aritmética é dada pela seguinte fórmula:
![]()
Passando essa fórmula pra Python:
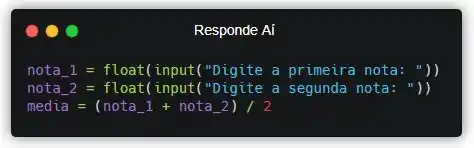
Agora, vamos exibir esse valor pro usuário!
Passo 3
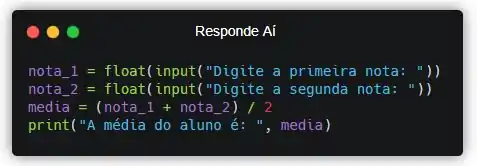
Pra exibir pro usuário, bora usar a função print().
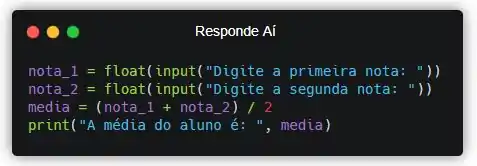
Pronto! Agora nosso programa calcula e exibe a média de um aluno. Não esqueça que a vírgula ali vai exibir os dois valores lado a lado. O texto e o valor dentro da variável “media”. Mas não esquece que isso só funciona na função print(), ok?! Cada função reage de uma forma diferente às vírgulas.
Resposta
Exercício Resolvido #8
Estácio, Linguagem De Programação – AV1; Adaptado
Que tipo de dado deve ser usado para armazenar um número do tipo: 65.890?
Passo 1
Fala aí! Cara, o próprio exercício já diz pra gente que é um número. Em Python só tem 3 tipos numéricos diferentes, que são: inteiro (int), real (float) e complexo (complex). Um desses três é a nossa resposta. Vamos analisar essas opções!

O tipo int não tem parte fracionária, apenas números inteiros, positivos e negativos. Por isso, não é a nossa resposta, já que o número do enunciado tem vírgula (parte fracionária).
Vamos analisar as outras!
Passo 2
O tipo complexo tem parte imaginária (raiz quadrada de -1). Esse tipo de número tem o seguinte formato:
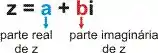
O nosso número não tem parte imaginária! Por isso, também não é um número complexo. Só nos resta uma opção!
Passo 3
O tipo float inclui todos os números reais. Isso é, número inteiro, positivo ou negativo e com parte fracionária. Descreve bem o número do enunciado, né?! Por isso, a resposta é float!

Resposta
Float