Lei da Velocidade
Produzido por Marcelo BrillantinoTeoria
Você lembra que a velocidade de uma reação é calculada de acordo com como a concentração de produtos/reagentes varia, né?
De uma maneira geral a velocidade de uma reação pode ser constante:
Ou ela pode depender da concentração dos reagentes e/ou produtos.
Por exemplo, vamos supor a reação:
Muitas vezes, quanto maior a concentração dos reagentes, maior a velocidade da reação.
Dessa forma, pode ser que a velocidade dependa da concentração de A:
Mas a dependência da velocidade com a concentração de pode ser de segunda ordem:
Ou de terceira, quarta, quinta...
E como que determinamos isso?
Experimentalmente!
Fazemos uma série de experimentos, mudando a concentração dos reagentes e medindo a velocidade.
Se encontrarmos algo como:
![]()
Percebemos que a velocidade é diretamente proporcional à concentração de no meio.
Pois ao dobrar a concentração, a velocidade dobra. Ao triplicar a concentração, a velocidade triplica, e assim sucessivamente.
Podemos, ainda, calcular o valor da constante , simplesmente dividindo a velocidade pela concentração em qualquer ponto da tabela.
E a unidade de vai ser dependente das unidades de e . No nosso exemplo seria .
Se os dados fossem do tipo:
![]()
Ao dobrar a concentração de , a velocidade quadriplica. E ao triplicar a concentração, a velocidade aumenta 9 vezes. Ou seja: a relação entre e é quadrática! E a Lei da velocidade fica:
Onde pode ser calculado por:
Olha aí como a unidade da constante mudou!
Aí existe a Lei da ação das massas (Lei de Guldberg-Waage) que diz que, para uma reação do tipo:
A lei da velocidade fica:
Ou seja:
“A velocidade da reação é diretamente proporcional à concentração molar dos reagentes elevadas aos seus respectivos expoentes.”
Mas isso só vale para reações elementares. Ou seja, quando a reação aconcentece em uma única etapa.
Muitas vezes, quando vemos a reação global, embora a gente não saiba, várias etapas ocorrem ali.
Por isso, via de regra, usamos os dados experimentais e não a lei de Guldberg pra formular a lei da velocidade de uma reação. Beleza?
Sério, especialmente se os dados estiverem tabelados.. não tenta fazer pela lei de Guldberg!
Ordem da reação
A ordem da reação é aquele numerozinho do expoente da lei da velocidade.
Aí existe a ordem em relação a determinada substância e a ordem global da reação.
Vamos ver como funciona. É bem simples.
Supondo a lei de velocidade:
Então a reação é de primeira ordem em relação ao e de primeira ordem em relação ao .
A ordem global é a soma de todas as ordens. Ou seja, será a soma dos expoentes das concentrações.
Nesse caso, a reação será de segunda ordem global.
Para o caso:
A reação é de segunda ordem em relação ao , de primeira ordem em relação ao e de terceira ordem global!
Não se assuste se encontrar ordem fracionária, igual a 0 ou negativa. Tudo isso pode acontecer.
Se a ordem global for zero, a velocidade não depende da concentração de nenhum dos reagentes. Então ela é igual a uma constante!
Bora fazer uns exercícios de fixação especialmente selecionados pra você?
E como que determinamos isso?
Ordem da reação
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Supondo uma reação com a seguinte lei de velocidade:
Responda:
a) Qual a ordem da reação em relação ao gás nitrogênio?
b) Qual a ordem da reação em relação ao gás hidrogênio?
c) Qual a ordem global da reação?
d) O que acontece com a velocidade da reação caso a concentração de seja dobrada?
e) O que acontece com a velocidade da reação caso a concentração de seja dobrada?
Passo 1
a) A ordem da reação em relação ao é o expoente ao qual a concentração de está elevada na fórmula.
Como [] tem um expoente “1” implícito ali, a ordem em relação ao gás nitrogênio é 1: de primeira ordem!
Passo 2
b) A ordem em relação ao é 3, pois esse é o expoente da concentração de na fórmula.
Passo 3
c) A ordem global da reação é a soma de todos os expoentes (que coincide com a soma de todas as ordens).
Ordem global é quatro.
Passo 4
d) Vamos lá... a velocidade da reação nas concentrações iniciais é:
Se a gente dobrar a concentração de , teremos um segundo valor de velocidade:
Que a gente pode reorganizar como:
Portanto, ao dobrar a concentração de a velocidade também dobra!
Passo 5
e) Mais uma vez, a velocidade da reação nas concentrações iniciais é:
Agora se e a gente dobrar a concentração de , teremos outro valor de velocidade:
Que a gente pode reorganizar como:
Portanto, ao dobrar a concentração de a velocidade aumenta oito vezes!
Passo 6
Obs: em relação às ordens, normalmente se fala primeira, segunda e terceira ordem. A partir desse valor, é mais comum dizer “de ordem quatro, de ordem cinco, de ordem seis...”.
Resposta
a) Primeira ordem
b) Terceira ordem
c) Ordem quatro
d) A velocidade dobra
e) A velocidade aumenta 8 vezes
Exercício Resolvido #2
Elaboração própria.
Foram feitos três experimentos, mantendo-se a temperatura constante, com concentrações diferentes dos reagentes A e B, medindo a velocidade da reação:
Os resultados podem ser vistos abaixo:

Qual a lei da velocidade da reação?
A reação é elementar?
Passo 1
A lei da velocidade da reação será algo como:
E o que precisamos fazer é determinar os valores de , e , a partir dos dados da tabela.
Passo 2
Começaremos usando duas linhas da tabela onde a não seja alterada. Com constante, estudamos apenas o efeito da concentração de A na velocidade.
No caso, vamos usar as linhas 2 e 3.
Agora dividimos por (ou o contrário). Dessa forma, vamos cortar as incógnitas e , e poderemos calcular .
Cortando o e o , que aparecem em cima e embaixo da fração e resolvendo a fração numérica:
Só mais um pouquinho de matemática:
Passo 3
Agora vamos usar as linhas 1 e 2, onde a concentração de é constante, tal que a gente pode estudar a influência da concentração de na velocidade.
Agora dividimos por (ou o contrário). Dessa forma, vamos cortar as incógnitas e , e poderemos calcular .
Simplificando, nos resta:
Passo 4
Por enquanto, a nossa lei da velocidade está:
Vamos, agora, calcular o valor da constante.
A constante é alterada por mudanças na temperatura. Como alterações de concentração não mudam a constante, podemos usar qualquer um dos 3 experimentos para calcular o valor de .
E não podemos esquecer da unidade da constante:
Onde é a unidade da constante (e não a concentração!!!).
Passo 5
Show!! Já encontramos nossa lei de velocidade da reação:
E agora, será que essa reação é elementar?
Ou seja: será que ela ocorre em uma única etapa??
A resposta certa é: NÃO!
Se a reação fosse elementar, a lei da velocidade coincidiria com a lei da velocidade proposta por Guldberg, lembra?
Ela deveria ser assim:
Como a lei da velocidade não é assim, a reação ocorre em mais de uma etapa!
Resposta
a)
b) Não é elementar
Exercício Resolvido #3
Elaboração própria.
Observe o gráfico abaixo:

Considere que o mesmo se refere à reação:
Prediga a lei da velocidade, a ordem global da reação e o que ocorre no tempo .
Passo 1
Como podemos ver no gráfico, inicialmente a velocidade é constante. Ou seja:
Dessa forma, já sabemos a lei da velocidade.
Isso significa que a velocidade independe da concentração do reagente . Afinal de contas, com o passar do tempo, a reação vai acontecendo, vai sendo consumido e a velocidade não é alterada.
Se a velocidade é constante, a reação é de ordem zero!
Passo 2
Se a velocidade é constante, independente da concentração de , o que que acontece no tempo igual a 7 minutos?
Bem, a velocidade independe da concentração do reagente desde que haja reagente no meio, né?
Se não tem reagente, não tem reação e a velocidade da reação vai a zero.
Isso que ocorre no tempo igual a 7 minutos. O reagente é totalmente consumido e a velocidade zera.
Resposta
Lei da velocidade: , onde .
Ordem global zero.
O reagente acaba.
Exercício Resolvido #4
USP – Curso de Farmácia. Lista de Cinética da Professora Denise Petri. Questão 02.
Os dados abaixo foram obtidos para a reação entre os reagentes A e B, formando o produto P. A partir destes dados, determine a ordem global da reação, a equação de velocidade e a constante de velocidade da reação.

Passo 1
A lei da velocidade da reação será algo como:
E o que precisamos fazer é determinar os valores de , e , a partir dos dados da tabela.
Passo 2
Começaremos usando dois experimentos onde a não seja alterada. Com constante, estudamos apenas o efeito da concentração de A na velocidade.
Podemos usar os experimentos 1 e 4, 1 e 5 ou 4 e 5. Como entre 1 e 4 a concentração de A dobra, pode ser mais fácil estudar o efeito da alteração de na velocidade. Mas você pode escolher fazer com qualquer um dos três pares.
Agora dividimos por (ou o contrário). Dessa forma, vamos cortar as incógnitas e , e poderemos calcular .
Cortando o e o , que aparecem em cima e embaixo da fração e resolvendo a fração numérica:
Só mais um pouquinho de matemática:
Se não der pra ver de cara o valor de , fatora o 4:
Passo 3
Agora vamos usar as linhas 1 e 2, onde a concentração de é constante e a concentração de B dobra.
Agora dividimos por (ou o contrário). Dessa forma, vamos cortar as incógnitas e , e poderemos calcular .
Simplificando, nos resta:
Passo 4
Por enquanto, a nossa lei da velocidade está:
O que nos diz que a ordem global da reação é:
Passo 5
E, agora, vamos calcular o valor da constante.
Como alterações de concentração não mudam a constante, podemos usar qualquer um dos 5 experimentos para calcular o valor de .
Vou pegar o primeiro pra fazer a conta!
E não podemos esquecer da unidade da constante:
Onde é a unidade da constante (e não a concentração!!!).
Resposta
Reação de terceira ordem global.
, onde
Exercício Resolvido #5
USP – Química Geral – SLC 0660. Lista de Exercícios IV. Questão 01.
Para a seguinte reação em fase gasosa foram obtidos os seguintes valores de velocidade inicial em função da concentração inicial dos reagentes. Com base nestes resultados, determine a lei de velocidade desta reação, a ordem total e estime o valor da constante de velocidade.
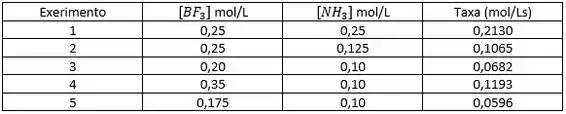
Passo 1
A lei da velocidade da reação será algo como:
E o que precisamos fazer é determinar os valores de , e , a partir dos dados na tabela.
Passo 2
Começaremos usando dois experimentos onde a não seja alterada. Com constante, estudamos apenas o efeito da concentração de na velocidade.
Podemos usar os experimentos 3 e 4, 3 e 5 ou 4 e 5. Como entre 4 e 5 a concentração de cai pela metade, pode ser mais fácil estudar o efeito da alteração de na velocidade. Mas você pode escolher fazer com qualquer um dos três pares.
Agora dividimos por (ou o contrário). Dessa forma, vamos cortar as incógnitas e , e poderemos calcular .
Cortando o e o , que aparecem em cima e embaixo da fração e resolvendo a fração numérica:
Só mais um pouquinho de matemática:
Passo 3
Agora vamos usar as linhas 1 e 2, onde a concentração de é constante e a concentração de é alterada.
Agora dividimos por (ou o contrário). Dessa forma, vamos cortar as incógnitas e , e poderemos calcular .
Simplificando, nos resta:
Passo 4
Por enquanto, a nossa lei da velocidade está:
O que nos diz que a ordem global da reação é:
Passo 5
E, agora, vamos calcular o valor da constante.
Como alterações de concentração não mudam a constante, podemos usar qualquer um dos 5 experimentos para calcular o valor de .
E não podemos esquecer da unidade da constante:
Onde é a unidade da constante (e não a concentração!!!).
Resposta
Reação de segunda ordem global.
, onde
Exercício Resolvido #6
James E. Brady e Gerard E. Humiston Volume 2, 2ª edição: Livros Técnico Científicos Editora. página 485 exercício 12.50
A lei de velocidade determinada para uma reação é:
Qual seria a Velocidade de reação, se:
- as concentrações de A e B fossem ?
- e
Passo 1
Lei de velocidade
Nesse caso a questão é bem simples: vamos apenas aplicar as concentrações dadas na lei de velocidade sem medo de ser feliz.
Passo 2
Lei de velocidade
Mais uma vez basta aplicar as concentrações dadas na equação de velocidade também dada.
Resposta
Exercício Resolvido #7
James E. Brady e Gerard E. Humiston Volume 2, 2ª edição: Livros Técnico Científicos Editora. página 485 exercício 12.50
A reação do com o segue a equação
Foram coletados os seguintes dados:

- Qual é a lei de velocidade para a reação?
- Qual é o valor da constante de velocidade?
Passo 1
Lei de velocidade
Ainda sem saber a lei de reação para a reação podemos supor que ela segue a seguinte equação:
A lei de velocidade é obtida experimentalmente verificando o efeito da concentração de cada reagente sobre a velocidade da reação.
Para o :
Analisando apenas as linhas 1 e 3 da tabela vê-se que ao dobrar a concentração desse reagente a velocidade da reação foi multiplicada por , ou seja

Com isso podemos montar as seguintes equações:
Equação 1
Equação 2
Realizando a divisão da equação 2 pela 1 termos que:
Seguindo a conta
Agora comparando as linhas 1 e 2 da tabela teremos as seguintes equações:

Com elas podemos montar as seguintes equações:
Equação 1
Equação 2
Realizando a divisão da equação 2 pela 1 termos que:
Logo
Então a lei da reação é
Passo 2
Achando o K
Basta agora substituir os valores em uma equação anterior.
Logo fazendo as contas teremos:
Resposta
Com