Cálculo de Concentração
Produzido por Marcelo BrillantinoTeoria
Opa, seja bem vindo ao Responde Aí! Hoje a gente vai bater um papo sobre o Cálculo de Concentração!
Imagina que você quer produzir o composto
Você então coloca os dois reagentes em um béquer e espera o tempo de reação! Mas…concorda comigo que com o passar do tempo os reagentes vão sendo consumidos e o produto sendo produzido, alterando a sua concentração?
E se eu quisesse saber a concentração do reagente em um tempo
Bora descobrir isso?! 👇👇👇
Ordem de Reação
A ordem de uma reação nos dá a relação entre a velocidade de reação e o consumo dos reagentes, da seguinte forma:
Onde
📢 Clique para ver mais:
Reação de Ordem Zero
Em uma reação de ordem zero temos:
Isso significa que a velocidade da reação é constrante! Então podemos dizer que:
Então nesse caso a variação da concentração pode ser calculada por:
O sinal negativo deve garantir que a concentração final seja menor do que a inicial. Afinal de contas, o reagente está sendo consumido.
Com essa equação a gente consegue achar a concentração em algum tempo específico!
Você também pode conferir esse conteúdo em vídeo:
Reação de Primeira Ordem
Para uma reação de primeira ordem, seguindo a mesma lógica, a velocidade da reação será:
E se a gente quiser saber a concentração do reagente em algum tempo específico?
A velocidade do consumo do reagente
Que pode ser reorganizado de uma forma que nos permita integrar dos dois lados, encontrando:
Resolvendo as integrais do tempo inicial ao final, considerando as concentrações inicial e final do reagente
Integrando chegamos em:
E agora, com a concentração inicial do reagente, podemos calcular a concentração dele depois de passado certo tempo
Reação de Segunda Ordem
Para uma reação de segunda ordem em relação a um reagente, a velocidade da reação será:
O consumo do reagente
Arrumando, temos:
Integramos os dois lados:
Colocamos os limites de integração:
Resolvendo chegamos em:
E, mais uma vez, podemos calcular a concentração do reagente conhecendo a concentração inicial e o tempo transcorrido!
Agora vamos praticar com exercícios?
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Considere a reação de primeira ordem:
a) Qual será a velocidade inicial da reação quando 10,00 g de reagem em um balão de 250,00 mL?
b) Qual será a concentração do reagente aos 5 minutos de reação?
c) Qual a velocidade da reação em ?
Considere que a reação ocorra a 700°C, temperatura na qual .
Passo 1
Bora resolver essa questão! Vamos começar vendo as informações que o enunciado está dando pra gente, beleza?
A primeira coisa que o enunciado diz pra gente que é que a reação é de primeira ordem. A gente tem que saber que pra reação de primeira ordem a velocidade de reação é descrita pela expressão:
Então, pro nosso caso:
Ali no finalzinho o enunciado diz também que à 700°C, que é a temperatura que a reação acontece.
Show, agora a que a gente sabe esses dados, o que que vamos precisar fazer pra resolver a questão?
Pra resolver a letra a, precisamos da concentração do reagente pra calcular a velocidade usando a fórmula!
Passo 2
Na letra a, o enunciado diz que são usados 10,00 g de e que o balão tem 250 ml. A concentração do reagente deve estar em mol/L.
Por isso, precisamos da massa molar do .
Considerando:
Show, agora podemos calcular a massa:
Dessa forma, o número de mols de reagindo vai ser:
Considerando o volume de reação :
Onde é a molaridade. Pode usar de concentração, ou como preferir!
Agora que temos e , bora calcular a velocidade inicial!
Passo 3
b) Aqui a gente quer saber a concentração do reagente com 5 minutos de reação.
Como a velocidade é a variação da concentração em função do tempo, temos que . Rearranjando os termos e integrando dos dois lados chegamos na seguinte expressão:
Que relaciona a concentração final e inicial do reagente , com a constante e o tempo. Na forma exponencial a expressão fica:
Considerando que o tempo inicial é 0 , ela permite que a gente calcule a concentração final do reagente, depois de certo tempo de reação.
Como nossa velocidade e nossa constante possuem unidades de segundo, temos que usar o tempo em segundos, ok?
Como já sabemos que e a concentração inicial do reagente é , bora então colocar isso na fórmula e calcular a concentração final do reagente!
Passo 4
Substituindo os dados que a gente tem:
Portanto, percorridos 5 minutos, a concentração do no meio equivale a 1,13 mol/L.
Passo 5
c) Agora aqui a questão quer saber qual a velocidade da reação no tempo de 5 minutos.
Para calcular a velocidade no , basta usar a fórmula da velocidade, que nem a gente fez na letra a, só que dessa vez usar a concentração de reagente nesse tempo, que calculamos na letra b!
Onde:
Substituindo:
Observe que uma concentração menor leva a uma velocidade menor!
Resposta
a)
b)
c)
Exercício Resolvido #2
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 574-Exemplo 14.4.
Quando o ciclo-propano () é aquecido em 500 °C (773 K), ele se transforma no isômero propeno. Os dados da tabela mostram as concentrações de ciclo-propano medidas em vários instantes diferentes, após o início da reação. Confirma que a reação é de primeira ordem em e calcule a constante de velocidade.
![]()
Passo 1
Sabemos que, para reações de primeira ordem, são válidos:
O que pode ser escrito como:
Portanto, para reações de primeira ordem, a relação entre o e o tempo de reação é linear!
Pra confirmar se a reação é de primeira ordem devemos traçar um gráfico entre versus o tempo.
Passo 2
Aplicando o logaritmo às concentrações fornecidas, temos:
![]()
Que pode ser lançado num gráfico:
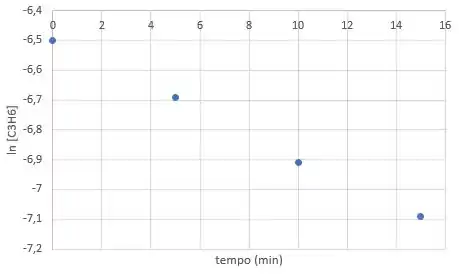
A relação parece linear né?
Então é de primeira ordem!
Passo 3
Pra calcular a constante, precisamos calcular o coeficiente angular do gráfico aí. Afinal:
E como fazemos isso?
Pelo gráfico, podemos fazer:
Vamos traçar uma reta aproximada dos pontos:
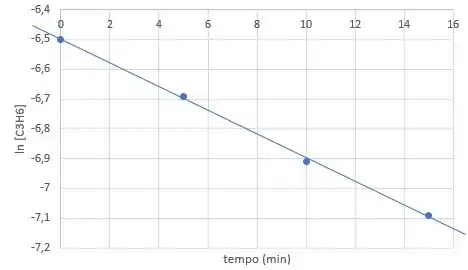
Escolher um intervalo e determinar o e :
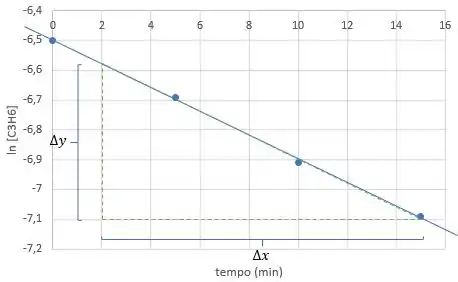
Os valores aproximados são:
Tal que:
Resposta
A reação é de primeira ordem, com .
Exercício Resolvido #3
USP – Lista de Exercícios de Cinética para o curso de Farmácia. Questão 04. Modificado.
Use a técnica da meia vida para determinar a ordem e a constante de velocidade a partir dos seguintes dados:
![]()
Obs: faça o gráfico de vs e verifique se independe de para ser de 1ª ordem. Se for dependente, faça o gráfico de vs para ver se é de 2ª ordem, etc...
Passo 1
Em um exercício anterior, pra verificar se a reação era de primeira ordem, a gente fez um gráfico de vs t. Porque, para reações de primeira ordem, esse gráfico nos leva a uma reta.
Outra característica das reações de primeira ordem é aquela questão da meia vida. Ou seja, para que a concentração caia pela metade, o tempo transcorrido é sempre o mesmo.
E aqui, vamos traçar o gráfico pedido (de vs ) e verificar a questão da meia vida pra ver se a reação é de primeira ordem.
Caso a meia vida não seja verificada, a gente testa o gráfico de segunda ordem e assim por diante.
Passo 2
Primeiro o gráfico!
Pra cada ponto, devemos calcular e depois aplicar o ln.
O que nos leva aos pontos:
![]()
A partir dos quais, montamos o gráfico:
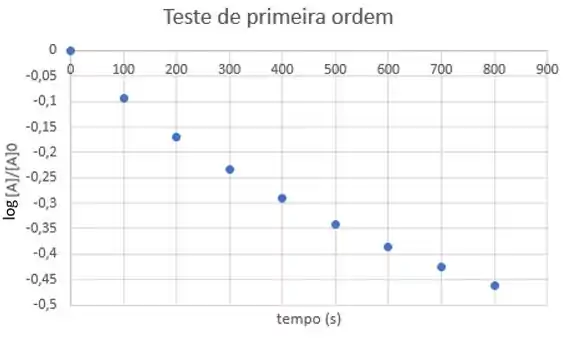
Se a gente tentar traçar uma reta com esses pontos, vai dar ruim!
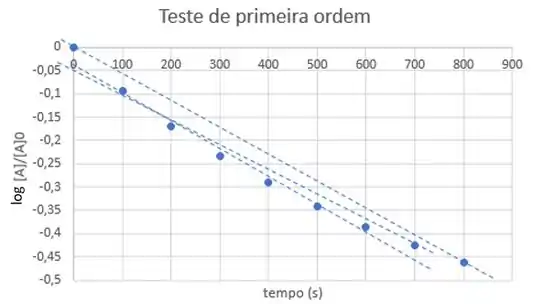
Nenhuma reta se adequa bem aos pontos.
Como, para uma reação de primeira ordem:
O gráfico de vs deveria ser uma reta com coeficiente linear zero e coeficiente angular igual a .
Se não tem reta, não é de primeira ordem!
Passo 3
Quanto à meia vida...
No período de meia vida, a concentração cai pela metade:
Quando o período de meia vida se processa novamente, a concentração cai para um quarto da inicial (metade da metade).
Portanto, o tempo transcorrido para o ln ir de a deveria ser o mesmo tempo transcorrido entre e .
Mas isso não é observado!
Em 400 s temos , mas em 800 s o não está nem perto de .
Como a questão da meia vida não é respeitada, confirmamos que a reação não é de primeira ordem!
Passo 4
Hora de testar a segunda ordem.
A gente deduziu que, para uma reação de segunda ordem:
Com e adotando a notação do exercício:
Ou seja, caso a reação seja de segunda ordem, o gráfico de 1/[A] vs t nos leva a uma reta!
Passo 5
Vamos preparar os pontos:
![]()
E traçar o gráfico!
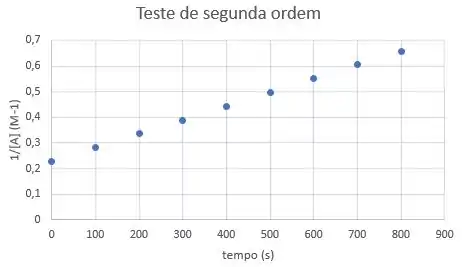
Hmm, agora sim parece uma reta! Conseguimos aproximar os dados por uma única reta!
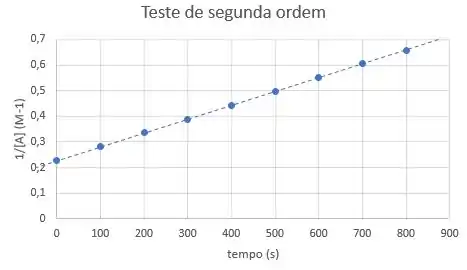
Portanto, a reação se comporta como de segunda ordem em relação ao reagente A.
Resposta
Comportamento de reação de segunda ordem em relação a A.
Exercício Resolvido #4
USP – Química Geral – SLC 0660. Lista de Exercícios IV. Questão 02.
O é um gás que se decompõe de acordo com a reação estequiométrica:
A variação da concentração de com o tempo a 300 °C é dada por:
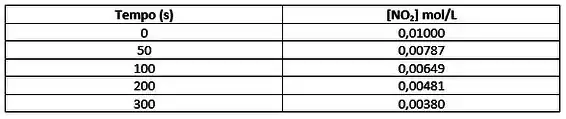
a) Verifique por método gráfico se a reação é de primeira ordem ou de segunda ordem.
b) Qual o tempo de meia vida para esta reação nas condições dadas?
c) Qual será a concentração de oxigênio após 400 segundos?
Passo 1
a)Em reações de primeira ordem:
Considerando , podemos simplificar para:
Portanto, podemos testar se uma reação é de primeira ordem traçando o gráfico de vs ou vs .
Em ambos os casos, caso a reação seja de primeira ordem, obteremos retas.
A diferença serão os coeficientes:
Vamos testar pela segunda equação. Você pode fazer com aquela que preferir!
Passo 2
Primeiro, preparamos os pontos:
Tal que:

O que nos leva ao seguinte gráfico:
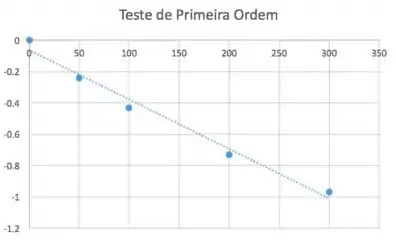
Cujos pontos se adequam mal a uma reta!
Vamos testar ela como de segunda ordem pra ver se ela se adequa melhor?
Passo 3
Para reações de segunda ordem:
Considerando :
Portanto, em reações de segunda ordem, obtemos uma reta ao traçar o gráfico de vs .
Bora lá!![]()
Que forma o gráfico:
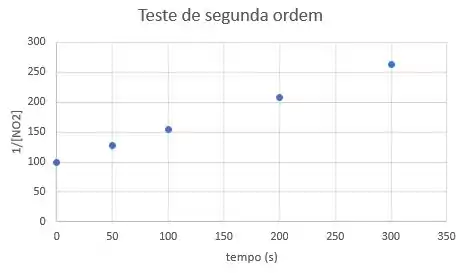
Agora sim, temos uma reta!
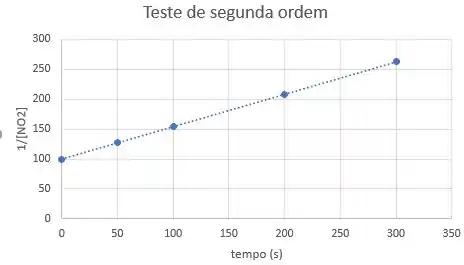
Como o gráfico de vs se adequa melhor a uma reta do que o gráfico de vs , a reação é de segunda ordem!
Passo 4
b) Para reações de segunda ordem, a meia vida depende da concentração inicial.
Dadas as condições iniciais do problema, o tempo transcorrido até que a concentração do reagente caísse pela metade pode ser definido pela reta que traçamos!
Quando:
Temos:
Assim:
O correspondente a será o .
E para descobri-lo, precisamos da equação da reta:
Onde:
E, pelo gráfico, vamos definir:
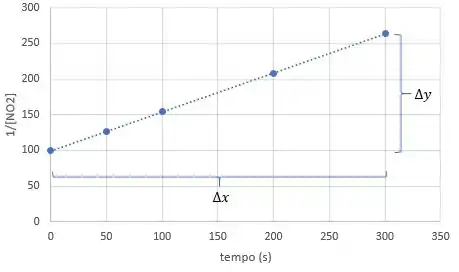
E para uma equação de segunda ordem, a unidade da constante é:
O que nos leva a seguinte equação da reta:
Tal que, para:
Teremos:
Passo 5
c) Atenção! Na letra c, o enunciado pede a concentração de OXIGÊNIO!
Vamos começar calculando a de :
Para :
Portanto, a quantidade consumida de foi de:
Como, a cada mol de consumidos, formamos meio mol de , podemos dizer que a concentração de após 400 segundos (considerando um recipiente fechado e tal), será:
Resposta
a) Segunda ordem.
b) 184,16 s.
c) 0,003425 mol/L
Exercício Resolvido #5
Elaboração própria.
Para as reações de ordem 0, 1 e 2, determine:
a) A lei de velocidade.
b) A lei de velocidade integrada.
c) O gráfico utilizado para verificar a ordem (identifique também os coeficientes).
Passo 1
a) A lei da velocidade de reações de ordem 0, 1 e 2 quanto a um reagemte hipotético podem ser escritas como:
Passo 2
b) Conforme definimos na nossa teoria, a partir da lei de velocidade das reações, podemos montar a lei de velocidade integrada. Olha aí:
Ordem 0:
Em uma reação de ordem zero, a velocidade é uma constante.
Tal que a variação na concentração do reagente será:
Organizando pra que a gente possa integrar:
Aplicando a integral do tempo inicial ao final, considerando as concentrações inicial e final do reagente:
Considerando que, normalmente, :
Ordem 1:
Tal que a variação na concentração do reagente será:
Organizando pra que a gente possa integrar:
Aplicando a integral do tempo inicial ao final, considerando as concentrações inicial e final do reagente:
Considerando que, normalmente, :
Que, usando as propriedades dos logaritmos, também pode ser expressa como:
Ou, ainda:
Ordem 2:
Tal que a variação na concentração do reagente será:
Organizando pra que a gente possa integrar:
Aplicando a integral do tempo inicial ao final, considerando as concentrações inicial e final do reagente:
Considerando que, normalmente, :
Que também pode ser expresso por:
Passo 3
c) De acordo com as equações que definimos acima:
- Caso a reação seja de ordem zero:
- Caso a reação seja de primeira ordem:
- Caso a reação seja de segunda ordem:
Tal que o gráfico de versus pode ser utilizado para verificar se uma reação é de ordem zero.
Para que isso seja provado, ao traçar tal gráfico devemos obter uma reta, cujos coeficientes serão:
Onde é o coeficiente angular e o coeficiente linear.
Tanto o gráfico de versus quanto o gráfico de versus tempo podem ser utilizados.
Em ambos os casos, teremos retas.
Quanto aos coeficientes das retas:
Onde é o coeficiente angular e o coeficiente linear.
O gráfico de versus deve gerar uma reta, de coeficientes:
Onde é o coeficiente angular e o coeficiente linear.
Resposta
a) ,
b) ,
c)
ou
Exercício Resolvido #6
Elaboração própria
Um composto químico , usado como contraste de exames de laboratório, tem meia vida de após ingerido. A dosagem mínima desse composto no organismo no momento do exame é de por quilo. Um paciente de após ingerir um comprimido de deve fazer o exame em no máximo quanto tempo?
Passo 1
Meia Vida
Só lembrando que meia vida é o tempo que leva para que uma determinada quantidade de um composto decaia para a sua metade.
Então, nesse caso, vamos precisar saber qual a concentração do composto no corpo do paciente assim que foi ingerido.
Logo:
Passo 2
Vamos simular as meias vidas
A cada meia-vida que passa, a concentração de A vai ser reduzida para a metade.
Primeira meia vida:
Após teremos : bastou eu pegar aquele valor inicial de concentração e dividir por 2.
Segunda meia vida:
Agora vamos dividir aqueles que sobraram antes por , e, após desde a ingestão do medicamento restaram exatos .
Assim, o exame pode ser feito em até 36 minutos após a ingestão do contraste.
Passo 3
Outra forma de se resolver esse tipo de questão é usando a fórmula para meia vida que é a seguinte:
Aí no nosso problema queremos descobirir o tempo que vai levar para que a quantidade final seja igual a e a massa inicial .
Simplifcando, ficamos com:
Que podemos reescrever da seguinte maneira:
Logo, nota-se que :
Portanto T = 36 minutos.
Resposta
36 minutos
Exercício Resolvido #7
Petrobrás, Prova para técnico de operações jr. 2011, questão 36
Hidrogênio e cloro em fase gasosa reagem formando ácido clorídrico. A reação inversa de dissociação também ocorre e, portanto, esse é um exemplo de uma reação homogênea e reversível em que a velocidade da reação direta é , e que a velocidade da reação inversa é .
Após certo intervalo de tempo, é estabelecido o equilíbrio químico desse sistema. Qual característica corrresponde à condição de equilíbrio desse sistema químico?
Passo 1
Quando é que uma reação está em equilíbrio?
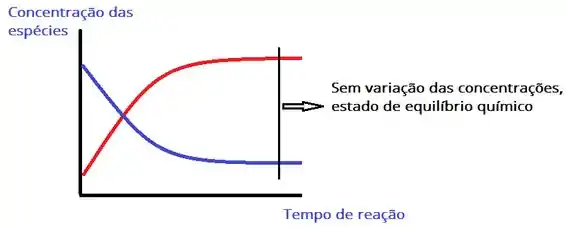
Uma reação está em equilíbrio quando não há mais variação nas concentrações das espécies químicas do sistema.
Assim, quando houver igualdade das duas velocidades de reação não observa-se mais formação efetiva nem de produtos e nem de reagentes.
Resposta
Letra C