Mecanismo de Reação
Produzido por Marcelo BrillantinoTeoria
Opa, seja muito bem vindo ao Responde Aí! Você sabe como prever o Mecanismo de Reação? Bora aprender!? 🤩
📢 Clique para saber mais:
- Mecanismo de Reação: Exercícios Resolvidos
- Fórmula da velocidade de reações químicas
- Modelos e Efeitos da Temperatura
O que é o Mecanismo de uma Reação?
Uma reação química pode ocorrer em uma ou várias etapas. O mecanismo de reação “divide” uma reação química em várias etapas elementares!
Caso você não se lembre, uma reação é dita elementar quando seus expoentes na lei de velocidade são os coeficientes estequiométricos da reação. Por exemplo, se liga nessa reação:
Ela é elementar se a velocidade de reação pode ser calculada usando assim:
Esse
Você também pode conferir esse conteúdo em vídeo:
Como Prever o Mecanismo de uma Reação
Vamos aprender como prever o mecanismo de uma reação fazendo um exemplo! Se liga nessa reação:
Experimentalmente, sua lei de velocidade foi calculada como:
Repara que essa reação não é elementar, pois os expoentes da lei da velocidade não são iguais aos coeficientes estequiométricos. Precisamos então dividir essa reação em reações elementares!
Uma parte vai ser em relação ao primeiro reagente e a segunda será uma forma de continuação. Assim:
A segunda reação, vai partir do produto da que está em cima, assim:
Tá vendo que o
Além disso, um outro detalhe importante quando um modelo é proposto, é propôr também qual seria a etapa lenta da reação. A etapa lenta é aquela que demora mais tempo para ocorrer, e por isso ela é também chamada de determinante: o resto da reação só vai poder acontecer depois que ela for realizada! No nosso exemplo a etapa lenta é:
Pois a reação só consegue continuar a acontecer devido ao
Mecanismo de uma Reação: Cinética
Da primeira equação, velocidade de formação de
Velocidade de consumo de
Da segunda equação, velocidade de consumo de
Podemos, então, calcular a velocidade líquida de formação de
Aí vem a grande sacada do problema! Lembra que o intermediário da reação é formado e rapidamente consumido? Nós supomos que ele está sendo totalmente consumido, e podemos então aproximar sua concentração a zero! Quando fazemos isso, a velocidade líquida se aproxima à
Assim, podemos encontrar:
Agora vamos pegar a equação de velocidade de formação do produto final, que é o
Substituindo a concentração de
À partir daí precisamos começar a fazer algumas aproximações! Por exemplo: como a velocidade da etapa lenta é sempre muito menor que das outras etapas, e nesse caso a etapa lenta é a equação
Ou seja:
Logo podemos retirar ele da equação porque é tão pequeno que não influência em nada, sendo assim:
E supondo que
Que é o que encontramos experimentalmente, o que comprova que o modelo está correto!
Agora vamos praticar com exercícios?
Como Prever o Mecanismo de uma Reação
Mecanismo de uma Reação: Cinética
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Considerando a reação elementar:
- Qual é a molecularidade dessa reação?
- Qual sua lei de velocidade?
- Em quais situações podemos prever a ordem de reação à partir da molecularidade?
Passo 1
a) Como a molecularidade depende do número de moléculas envolvidas para que a reação ocorra e sabemos que nesse caso precisamos de 2 moléculas de NO para formar o produto, a molecularidade é 2!
A reação, portanto, é bimolecular.
Passo 2
b) Como a reação é elementar, sua lei de velocidade usa o coeficiente estequiométrico como expoente:
Apesar de sabermos a sua lei de velocidade à partir da equação, é importante lembrarmos que o k deve ser sempre determinado experimentalmente, ein!
Passo 3
c) A ordem da reação da equação do exemplo é 2, né?
E a molecularidade também... Pois é, não é coincidência! Quando temos uma equação elementar, a molecularidade e a ordem de reação são de mesmo número... Então podemos prever a ordem de reação à partir da molecularidade quando a equação é elementar!
Vamos ver mais uns exemplos:
Molecularidade: 1 (reação unimolecular)
Lei da velocidade: v = k[SO3]
Ordem da reação: 1
Molecularidade: 2 (reação bimolecular)
Lei da velocidade: v = k[NO][Cl2]
Ordem da reação: 2
Resposta
- A reação é bimolecular
- Quando a reação é uma reação elementar podemos prever sua ordem de reação à partir da molecularidade
Exercício Resolvido #2
Elaboração própria
O seguinte mecanismo foi proposto para uma reação:
- Qual é a reação global e qual o intermediário de reação?
- Escreva a lei de velocidade e a molecularidade de cada etapa.
Passo 1
a) Para achar a reação global, temos que somar as duas equações 😊
Uma dica para saber se a reação está certa é conferir seu balanceamento.
Como o NO2 é formado na primeira etapa e consumido na segunda, ele é o intermediário da reação e não entra na reação global! Já o é o catalisador, já que ele é consumido na primeira reação e produzido na última. Se quiser representar ele na global é só fazer
Pra indicar que é o catalisador.
Passo 2
b) Etapa 1:
E como para a reação ocorrer precisamos de 1 molécula do O3 e uma de NO, a reação é bimolecular.
Etapa 2:
Mesmo caso da etapa 1, 2 moléculas são necessárias para a reação ocorrer, então a molecularidade é 2 (reação bimolecular).
Resposta
- Reação global:
- Ambas as reações são bimoleculares e suas leis de velocidade são:
E o intermediário de reação é o NO2
Etapa 1:
Etapa 2:
Exercício Resolvido #3
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp605-Exercício 14.51
Foram propostos três mecanismos para a reação :
Qual o mecanismo concorda com a segunte lei da velocidade: Velocidade ?
Passo 1
Vamos começar com o primeiro mecanismo!
- Se a reação fosse elementar (e ocorresse em só uma etapa), a velocidade da reação seria:
- Como a etapa lenta é , sua lei de velocidade é:
- A etapa lenta do mecanismo é , o que nos dá uma lei de velocidade:
Podemos ver que não corresponde à lei de velocidade experimental, já que a lei experimental diz que
Então esse modelo de mecanismo não está correto ꟷ a reação não é elementar.
Passo 2
Vamos tentar resolver primeiro através da lei determinante da velocidade, isso é, olhando a lei de velocidade da etapa lenta de cada um dos mecanismos!
O que corresponde à lei encontrada experimentalmente! Logo, esse mecanismo concorda com a lei de velocidade da reação.
Essa lei difere da lei encontrada experimentalmente, logo o mecanismo não concorda!
Passo 2
Esse passo na verdade é opcional ahahah Resolvendo pelo outro método e analisando mais a fundo o mecanismo, chegamos na mesma resposta! Então é só um adendo, se você quiser fazer de outra maneira:
B) Para saber se esse mecanismo está correto, começamos com a lei de velocidade líquida do intermediário de reação.
![]() Para identificar quem é o intermediário, precisamos lembrar que o intermediário é produzido numa etapa e consumido na etapa seguinte, e que não aparece na reação global! Se somarmos as duas etapas vamos obter:
Para identificar quem é o intermediário, precisamos lembrar que o intermediário é produzido numa etapa e consumido na etapa seguinte, e que não aparece na reação global! Se somarmos as duas etapas vamos obter:
Nesse caso, o intermediário é o NO3.
Velocidade de produção do NO3:
Velocidade de consumo do NO3:
Velocidade líquida de formação de NO3:
Daí vem a grande sacada que temos que fazer nesse tipo de problema! Vamos supor que tudo que é produzido na etapa 1 é consumido na segunda etapa. Com essa suposição a equação acima é zerada, e a nova equação fica:
Depois, precisamos calcular a velocidade de formação do produto final (nesse caso, vamos usar o CO2), encontrada na etapa 2:
Essa velocidade de formação é a encontrada experimentalmente (e que precisamos saber se o modelo se adequa à ela).
Usando as duas equações encontradas até agora:
Podemos, então, concluir que o modelo se adequa ao encontrado experimentalmente!!! 😊
C)
![]()
Já calculamos, para o mecanismo 2, a velocidade de formação e consumo do intermediário. Porém tem um detalhe: no mecanismo 2 não tínhamos o equilíbrio. Então precisamos repensar a velocidade líquida que calculamos.
Velocidade de produção do NO3:
Velocidade de consumo do NO3:
Então a equação de velocidade líquida de formação do NO3 será:
Fazendo a mesma suposição do passo 2... (que tudo o que é produzido é consumido):
Ao mesmo tempo, pela velocidade de produção do produto final (CO2) :
Usando as duas equações encontradas até agora:
Vemos que a
O que não corresponde ao modelo encontrado experimentalmente!
Resposta
O modelo que concorda com a lei de velocidade proposta é o B.
Exercício Resolvido #4
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp605-Exercício 14.52
Quando a velocidade da reação foi estudada, descobriu-se que a velocidade dobrava quando a concentração de O2 dobrava, mas ela quadruplicava quando a concentração de NO dobrava. Qual dos seguintes mecanismos está de acordo com essas observações? Explique seu raciocínio.
a)
Etapa 1:
Etapa 2:
b)
Etapa 1:
Etapa 2:
Etapa 3:
Passo 1
Antes de verificar qual mecanismo proposto é o melhor para essa reação, precisamos descobrir qual a lei de velocidade foi encontrada experimentalmente!
Para isso, precisamos só analisar o enunciado. Como o enunciado diz, a velocidade dobra quando [O2] dobra, então eles tem uma reação linear (expoente 1 na lei de velocidade). Já com a [NO], quando dobramos a concentração, a velocidade quadruplica, o que significa um expoente 2 na lei de velocidade.
A lei de velocidade é, então:
Passo 2
Analisando o mecanismo A proposto...
A reação global desse mecanismo é:
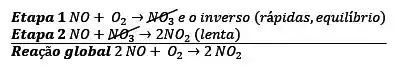
Sabemos que o intermediário da reação é NO3, e sua lei de formação líquida é:
Usando aquela aproximação esperta, considerando que tudo que é formado é consumido, podemos considerar que a velocidade líquida de formação é 0! Daí a equação acima fica:
Já a equação que queremos, que é a de produção de NO2, é retirada da etapa 2 e é:
Para relacionarmos essas duas equações, precisamos de mais uma aproximação! Como a etapa 2 é a etapa lenta, sua velocidade é beeeeeeem menor que a velocidade da etapa 1 (que é a etapa rápida) e, portanto, sua constante de velocidade também!
Assim, podemos supor que:
, logo
Usando essa aproximação na equação que achamos para [NO3],
E, substituindo na velocidade do produto final:
Onde
Podemos ver então que o mecanismo A está de acordo com a lei de velocidade encontrada experimentalmente!
Resposta
O mecanismo A
Exercício Resolvido #5
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 14.61
A reação obedece à lei de velocidade: . O seguinte mecanismo foi proposto para essa reação:
- Qual seria a lei de velocidade se a primeira etapa fosse a etapa determinante da velocidade?
- Com base na lei de velocidade observada, o que você pode concluir sobre as velocidades relativas das duas etapas?
Passo 1
Vamos começar com a letra a!
- Se a primeira etapa fosse a etapa determinante da velocidade, ou seja, a etapa lenta, a lei de velocidade da reação global seria escrita à partir de sua lei de velocidade.
- Podemos ver de cara que a etapa 2 também não é determinante da velocidade, mas isso não quer dizer que não existe uma etapa lenta (lembrando que a definição de etapa lenta da reação é a etapa com maior energia de ativação).
Isso quer dizer que a lei de velocidade da reação global seria:
Passo 2
Podemos, porém, pensar um pouquinho nas duas etapas e analisar a lei experimental da velocidade...
Como a relação com a [NO] é quadrática, e na etapa 1 isso é impossível de acontecer, a etapa lenta tem que ser a etapa 2, que é mais decisiva na lei da velocidade que a etapa 1.
Todas essas suposições são facilmente verifícaveis!
Se analisarmos a formação/consumo do intermediário de reação (NOCl2), obtemos:
Sua velocidade líquida de formação é, portanto:
Se pensarmos que tudo que produzimos do intermediário de reação é produzido, podemos fazer a aproximação:
E
Como presumimos a etapa 2 como etapa lenta,
, e
De onde podemos obter:
Já a equação de formação do produto final (NOCl) é:
Substituindo a [NOCl2] nessa velocidade obtemos:
Assim, provamos o que tínhamos suposto lá em cima! De fato a etapa 2 é a lenta 😊
Resposta
- A etapa 1 é a etapa rápida (com um equilíbrio químico) e a etapa 2 é a etapa lenta.
Exercício Resolvido #6
Adaptada de BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 14.62
Você estudou a oxidação na fase gasosa de HBr por O2:
Você descobre que a reação é de primeira ordem em relação a HBr e de primeira ordem em relação a O2. Você propõe o seguinte mecanismo:
- Com base na lei da velocidade, qual etapa é determinante da velocidade?
- Se você não for capaz de detectar HOBr ou HOOBr entre os produtos, isso contradiz seu mecanismo?
Passo 1
- O primeiro passo é descobrir qual a lei da velocidade dessa reação! Como o enunciado diz que ela é de primeira ordem em relação a HBr e a O2, sua velocidade é dada por:
- Como o HOBr e o HOOBr são intermediários da reação e ambos são consumidos em etapas rápidas, por mais que eu não os detecte no meio não quer dizer que o meu mecanismo esteja errado, pois eles podem estar sendo consumidos assim que são formados.
A etapa determinante desse processo é a etapa 1, que tem como lei de velocidade a mesma lei da reação global, logo, ela é a etapa lenta que define a lei da velocidade da reação.
Passo 2
Resposta
- Etapa 1
- Não, e sim que eles são intermediários que só participam de etapas rápidas.
Exercício Resolvido #7
James E. Brady e Gerard E. Humiston Volume 2, 2ª edição: Livros Técnico Científicos Editora. página 484 exercício 12.23
A reação,
Parece ter o mecanismo (a baixa temperatura)
Etapa Lenta
Etapa Rápida
Explique por que a reação é de ordem zero, com respeito ao .
Passo 1
Aqui vamos precisar lembrar que em uma reação feita de várias etapas a cinética depende sempre da etapa lenta, essa etapa é a que determina a lei de velocidade. Com isso nesse mecanismo proposto a lei de velocidade mostra dependencia apenas das concnetrações do e com isso a a reação apresenta ordem nula para o
Lei de velocidade para esse mecanismo seria:
Resposta
O mecanismo de reação leva em conta apenas a etapa lenta e por isso a lei de velocidade dessa reação não apresenta depedencia da concentração de de