Modelos e Efeitos da Temperatura
Teoria
Os modelos de reações servem pra tentar explicar o que acontece fisicamente durante uma reação – e assim justificar os valores de constante de velocidade que achamos (e porque esse valor varia de reação pra reação)...
Não é tão complicado assim, vamos por partes que fica tranquilo!
Efeito da temperatura e Equação de Arrhenius
É experimentalmente comprovado que quando a gente aumenta a temperatura, a velocidade da reação aumenta também!
Um químico chamado Arrhenius conseguiu descobrir (através de váaarios experimentos), que a relação entre a constante de velocidade e a temperatura pode ser descrita pela seguinte reação, chamada Equação de Arrhenius:
Ou então:
Onde R é a constante universal dos gases e A e Ea são duas constantes definidas experimentalmente beem importantes! O A é o fator pré-exponencial, e na verdade ele é mais matemático que qualquer outra coisa! Mas o Ea é a energia de ativação, e tem um sentido químico interessante!
A energia de ativação é a energia mínima necessária para que uma reação ocorra!
Teoria das colisões
Essa teoria se baseia na teoria cinética dos gases é bem intuitiva! Vamos considerar uma reação:
Vamos imaginar que as moléculas de X e Y estão circulando no meio, cada uma com sua energia cinética. Segundo essa teoria, três coisas devem acontecer simultaneamente para que a reação aconteça:
- Uma molécula de X e uma de Y devem colidir,
- Essa colisão deve ocorrer numa orientação adequada para que a colisão seja efetiva (gere um produto),
- As moléculas devem ter energia suficiente para que as ligações químicas sejam quebradas/formadas!
A 1ª condição é fácil de entender, né? Para que a reação ocorra, é preciso que as moléculas se encontrem! A 2ª condição é fácil de explicar com uma imagem:
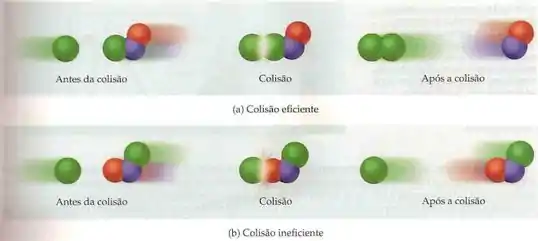
A 3ª condição é a mais importante! Tem uma metáfora bem clichê pra explicar essa teoria, mas que funciona: imagina que as moléculas de X e Y são duas bolas de sinuca. Quando elas se chocam, se elas tiverem uma energia menor do que a suficiente para que a reação ocorra, elas vão se chocar e ir cada uma pro seu lado.
Se elas tiverem uma energia maior ou igual do que a energia necessária, elas se chocam e despedaçam! Agora imagina que esse “despedaçar” são as ligações químicas sendo quebradas/formadas e pronto! A reação pode acontecer! 😊
Essa barreira energética que os reagentes precisam superar (a gente viu até agora como energia mínima para a reação acontecer) é a famosa energia de ativação!
Teoria do estado de transição (ou complexo ativado)
Essa teoria veio pra completar a teoria das colisões! Ela usa os mesmos princípios e os 3 critérios da teoria das colisões devem ser atendidos, mas existe uma diferençazinha.
Na teoria das colisões, quando os 3 critérios são atendidos, a reação ocorre e o produto é formado. Na teoria do estado de transição, o que se forma não é o produto diretamente, mas uma espécie que não é nem produto nem reagente, o tal estado de transição ou complexo ativado!
E o que seria esse estado? Vamos ver graficamente que fica mais simples:
Considerando a reação:
Podemos considerar como estado de transição o momento onde nem a ligação AꟷA e BꟷB foram quebradas, nem as ligações AꟷB foram formadas!
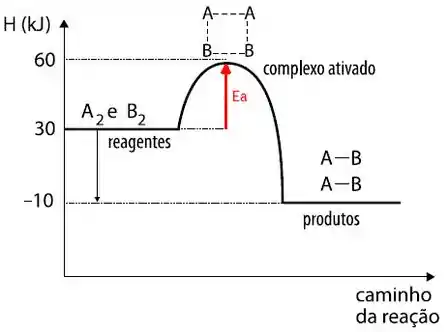
Um detalhe importante sobre o estado de transição é que ele não pode ser isolado. Ou seja, ele é uma espécie química teórica, não conseguimos vê-lo na reação nem analisá-lo em laboratório.
Obs: esse gráfico é beeeeem importante porque com ele dá pra entender melhor como funciona a energia de ativação! Se os reagentes não tem energia suficiente para passar esse pico no gráfico, a reação fica nos reagentes. Se eles conseguem passar, forma-se o complexo ativado e, em seguida, os produtos!
Vamos exercitar?
Teoria das colisões
Teoria do estado de transição (ou complexo ativado)
Exercícios Resolvidos
Exercício Resolvido #1
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 606-Exercício 14.59
A constante de velocidade da reação de primeira ordem é de em e em . Calcule a energia de ativação da reação, sabendo que .
Passo 1
O primeiro passo é relembrar nossa queridíssima Equação de Arrhenius:
Que também pode ser escrita assim:
E o que significa cada elemento da equação?
O k é a constante de velocidade, o A é o fator exponencial de Arrhenius, o R é a constante dos gases e o T a temperatura.
Como a temperatura é dada em Kelvin, vamos trabalhar com o valor de R do SI e usar .
Aí vamos substituir os valores dados na equação de Arrhenius e resolver um sisteminha de duas equações pra calcular , a energia de ativação da reação, que é uma constante em relação à temperatura.
Bora lá.
Passo 2
Substituindo os valores dados:
A 1000 K:
Para a reação 2:
Chegamos a um sistema com duas incógnitas e duas equações para resolver!
Passo 3
Arrumando um pouco as equações, temos:
Subtraindo uma equação da outra:
Resposta
A energia de ativação da reação é de 39,7 KJ/mol.
Exercício Resolvido #2
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 606-Exercício 14.64
O etano, se dissocia em radicais metila a com constante de velocidade . Determine a constante de velocidade em sabendo que a energia de ativação da reação é
Passo 1
O primeiro passo é lembrar a equação de Arrhenius:
A temos:
De onde tiramos:
Passo 2
Usando o A encontrado no passo 1 podemos calcular o k da reação a .
Fazendo as contas, obtemos:
Resposta
A constante de reação a é .
Exercício Resolvido #3
Elaboração própria.
A figura abaixo apresenta 2 experimentos realizados para estudar graficamente a Equação de Arrhenius.
- As duas retas representam reações diferentes. Como podemos provar isso?
- Qual das duas reações tem uma maior energia de ativação?
Passo 1
Esse exercício é super importante para entendermos como funcionam os gráficos que descrevem a equação de Arrhenius!
Vamos lembrar a equação:
Se pensarmos que, para uma mesma reação, e são praticamente invariáveis com a temperatura e que é uma constante, podemos pensar na equação como:
Com isso na cabeça, bora resolver o que o enunciado pede.
Passo 2
a) Sobre a inclinação da reta:
A gente acabou de ver que a inclinação das retas representam . Como é uma constante, o que vai mudar de uma reta para outra é a energia de ativação. A energia de ativação é própria de uma reação, cada reação vai ter a sua. Se duas reações tem inclinações diferentes, elas vão ter energias de ativação diferentes, sendo, assim, duas reações diferentes!
Passo 3
b) Mais uma vez o enunciado tá perguntando sobre a energia de ativação, então temos que olhar pra inclinação da reta.
Ter uma energia de ativação maior significa que o termo vai ser maior. Logo, a reta “cai mais rápido”, tem uma maior inclinação. Qual reta tem maior inclinação?
Se você pegar um intervalo de vai ver que o varia mais para a reta azul do que pra vermelha, o que significa que ela tem uma inclinação maior! Logo a reta azul representa uma reação com maior energia de ativação!
Resposta
- Podemos provar através das diferentes inclinações na reta (o que indica energias de ativação diferentes).
- A reta azul (número 1)
Exercício Resolvido #4
Lista de exercícios UFPR – Prof Eduardo Lemos de Sá
A reação química entre acetato de etila e o íon hidroxila produzindo etanol e o íon acetato, foi estudada em diversas temperaturas, conforme mostrado abaixo.
Pede-se:
- Determine o valor da energia de ativação e do fator pré-exponencial.
- Estime o valor da constante de velocidade na temperatura de .
Passo 1
a) Relembrando a equação de Arrhenius:
Aplicando ln dos dois lados:
Aí tem duas formas de fazer: a primeira é por regressão linear, usando todos pontos, e a segunda é usando só duas temperaturas ali de cima, pra resolver por sistema.
Relaxa que vamos fazer juntos dos dois jeitos.
Passo 2
Pra fazer por regressão linear:
Repara que essa equação daqui:
É uma reta!
Então se você traçar os valores de versus os valores de vai encontrar uma reta de coeficiente linear igual a e coeficiente angular igual a .
A gente começa por calculando os valores de x e y a partir da tabela dada:
Aí você vai fazer uma regressão linear com esses dados na calculadora científica, que já te dá direto os valores de coeficiente linear e angular da reta formada pelos pontos que você informou pra ela.
Fazendo isso, vamos encontrar:
O que só nos confirma que os dados realmente formam uma reta!
Como:
Então:
E, dado que:
Vamos ter:
Esse método é “mais correto” porque utiliza todos os pontos dados. Você só precisa tomar cuidado com as unidades: vai ter a mesma unidade do seu e vai ter unidades dependendo do seu . Aqui usamos , por isso que nossa ficou nessa unidade.
Agora se regressão linear não é com você, você pode usar apenas dois pontos pra encontrar os valores de e . Pega o passo 3 aí.
Passo 3
Agora vamos precisar de dois pontos quaisquer. Vamos escolher os pontos onde e .
Passando essas temperaturas para , temos:
Substituindo os valores de e na equação de Arrhenius:
Organizando, obtemos:
Subtraindo a 2ª equação da 1ª :
Que equivale a:
Substituindo na primeira equação do sistema:
E:
Repara que tem que ter a mesma unidade que , já que o termo da exponencial necessariamente não tem unidade e:
Passo 4
b) Agora que já temos e , já podemos calcular o para ():
Usando os valores encontrados pela regressão linear:
Assim, o de é . Se a gente olhar na tabela, esse valor está entre os valores de para e , o que é coerente.
Resposta
- Energia de ativação =
Exercício Resolvido #5
Elaboração própria
Levando em consideração a teoria do complexo ativado, podemos afirmar que o complexo ativado:
- possui menos energia que os reagentes ou os produtos.
- sempre forma produtos.
- é um composto estável.
- possui mais energia que os reagentes ou os produtos.
Passo 1
a) Para analisar a letra a, vamos dar uma olhada nessa imagem aqui de baixo:
O complexo ativado é uma espécie hipotética que se encontra no meio do caminho reacional, onde nem as ligações dos reagentes foram completamente quebradas, nem as ligações dos produtos foram completamente formadas.
Ele é uma espécia beeeem energética. Inclusive, a energia de ativação é a diferença de energia entre a energia dos reagentes e a energia do complexo ativado, representando aquela barreira energética que a gente tem que vencer pra reação acontecer.
A partir disso, concluímos que a letra a é falsa! O complexo ativado possui mais energia que os reagentes e os produtos.
Passo 2
b) O complexo ativado só vai virar produto se as moléculas envolvidas tiverem energia suficiente para isso! Ou seja, se as moléculas tiverem uma energia maior ou igual à energia de ativação, elas tem energia suficiente para romper 100% as ligações entre reagentes e formar 100% as ligações dos produtos. Essa condição indica que nem sempre o complexo ativado vai virar produto.
Passo 3
c) Mais uma vez, uma imagem diz mais que mil palavras ahahah:
Como podemos ver, o complexo ativado é um estado teórico de transição – ele não é nem produto nem reagente, e nem conseguir isolar ele na reação a gente consegue! Por isso, ele não é estável, essa alternativa é falsa.
Passo 4
d) Quando discutimos o item a, já vimos que essa alternativa é verdadeira. O completxo ativado tem, sim, maior energia que os reagentes e que o produto.
Resposta
Letra D.
Exercício Resolvido #6
Elaboração própria.
A partir da Teoria das Colisões, explique qual dos 3 casos resulta em produto e por que:
Passo 1
Para responder essa questão, vamos lembrar as 3 condições da teoria das colisões:
- Os reagentes devem se chocar/colidir
- Essa colisão deve ter uma orientação específica boa para que a reação ocorra
- Eles devem ter energia suficiente para romper as ligações dos reagentes e formar as dos produtos – a tal energia de ativação.
Em todos os três casos a 1ª condição é satisfeita! Porém, somente no caso III as outras duas condições são satisfeitas!
Assim, somente o caso III tem um choque efetivo – um choque que resulta em uma reação bem sucedida – e somente ele vai resultar em produto!
Resposta
O caso III, pois somente nele os reagentes se chocam com a orientação certa e com energia suficiente – resultando num choque efetivo.
Exercício Resolvido #7
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 609-Exercício 14.106
O seguinte perfil de reação esquemático descreve a reação .
- A reação total é exotérmica ou endotérmica?
- Quantos intermediários existem? Identifique-os.
- Qual é a etapa determinante da velocidade da reação?
- Qual é a etapa mais rápida? Explique sua resposta.
Passo 1
É suuuuper importante saber ler esses gráficos! Vou dar um exemplo aqui de como ler, e a gente só aplica o que tá no exemplo no exercício:
a) O que determina se uma reação é endo ou exotérmica é a energia dos reagentes e dos produtos. Se a energia dos produtos for maior que a dos reagentes, a reação é endotérmica e precisa que energia seja doada para acontecer. Se a energia dos reagentes for maior que a dos produtos, a reação é exotérmica e ela libera energia.
Mas preste atenção: não é porque uma reação é exotérmica que sua energia de ativação é baixa! Analisar a energia de ativação é diferente de ver se a reação é exo ou endotérmica, ein!
A partir do gráfico do enunciado já podemos ver que a energia do reagente (A) é mais alta que a dos produtos (D), o que indica que a reação é exotérmica!
Passo 2
b) Os intermediários de reação SÃO DIFERENTES dos complexos ativados! Intermediários são espécies isoláveis e estáveis, que aparecem no caminho reacional e são consumidas em seguida...
Vendo mais uma vez no gráfico, temos 2 intermediários: o B e o C, que aparecem no meio reacional, são estáveis (tem energia relativamente baixa) e são isoláveis.
Se fossemos analisar esse gráfico pela teoria do complexo ativado, teríamos 3 complexos ativados: um em cada pico de energia de ativação.
Passo 3
c) A etapa determinante da reação é a etapa mais lenta – e a que tem a maior energia de ativação. Daí é só a gente ver no gráfico qual a maior energia de ativação: a etapa .
Passo 4
d) Já a etapa mais rápida vai ser o contrário – é a etapa com a menor energia de ativação! A Percebe que o menor pico está entre A e B. Masss, ainda que o pico entre C e D seja um pouquinho maior, C tá um pouco mais alto que os reagentes, o que faz com que a Energia de ativação de C para D seja menor do que a de A para B. Com menor energia de ativação, a etapa é a mais rápida.
Resposta
- Exotérmica.
- Sim, o B e o C são os intermediários dessa reação.
- A etapa , que tem a maior energia de ativação.
- A etapa , que tem a maior energia de ativação.
Exercício Resolvido #8
James E. Brady e Gerard E. Humiston Volume 2, 2ª edição: Livros Técnico Científicos Editora. página 484 exercício 12.29
Uma etapa do mecanismo para a decomposição do em e parece ser a:
Dada a estrutura do
Mostre como a orientação molecular de uma colisão pode ser importante na determinação do fato dos produtos serem formados.
Passo 1
Dado que uma etapa do mecanismo tem o reagindo com formando , para que a reação ocorra, o precisa se aproximar do pelo “lado do ”.
Tipo assim:
Quando o se aproxima da molécula por qualquer outro canto, a colisão não vai ser efetiva, porque os produtos não serão formados.
Essa imagem aí mostra colisão não efetiva para a reação.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #9
Prova da petrobras, Cargo engenheiro Jr. maio de 2010, Questão 49
As substâncias A e B se decompoem a com energias de ativação iguais a e , respectivamente. Se R representa a constante universal do gases, sendo e os fatores pré-exponenciais da lei de Arrhenius, a razão entre as velocidades específicas de decomposição de A e B é
Passo 1
Pra resolver essa questão, a gente precisa conhecer duas equações: a da velocidade de uma reação e a lei de Arrhenius.
A velocidade de uma reação é dada por:
Onde a velocidade de uma reação depende de uma constante de velocidade e da concentração de reagentes em algum grau n.
E essa constante de velocidade aí varia com a temperatura conforme a lei de Arrhenius, assim ó:
Onde é a energia de ativação, é a constante universal dos gases, é a temperatura em Kelvin e é o fator préexponencial, que o enunciado chama da e .
Então, o que o enunciado nos pede é aplicar essas relações para as reações de decomposição de e fazer uma razão entre a velocidade dessas reações.
Lembrando que tudo se passa a . Ou seja:
Bora?
Passo 2
Primeiramente, o enunciado nos fala de uma “velocidade específica” que é a velocidade mesmo por mol de reagentes. Nesse caso, podemos escrever que:
Aí colocamos de acordo com a lei de Arrhenius e temos:
E, usando a mesma nomenclatura do enunciado:
Para a reação de decomposição de A:
E para a reação de decomposição de B:
Passo 3
Agora precisamos fazer a razão entre e . Saca só:
Que, simplificando, fica:
Ou seja:
Resposta
Letra E