Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 19.Exercício - Ex. 30
Dê a estrutura do produto principal formado nas seguintes reações de condensação:
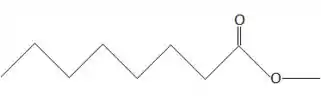
- ácido octanóico com metanol;
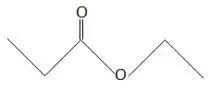
- ácido propanóico com etanol;
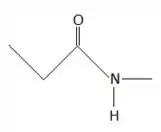
- ácido propanóico com metilamina;
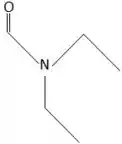
- ácido metanóico com dietilamina.
Passo 1
Fala aí! Vamos fortalecer nossos conhecimentos? Vamos lá!
O exercício quer que a gente dê a estrutura do principal produto dessas reações aí de cima, show?
Vamos começar com a letra a, temos um ácido carboxílico com um álcool, o produto de uma reação assim é um éster, e de cada lado teremos a quantidade de carbono de cada termo beleza?
Então a estrutura dele fica assim olha:
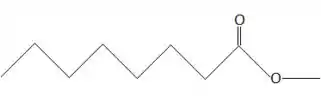
Passo 2
Na letra b temos temos um ácido carboxílico com um álcool, também, então vamos fazer a mesma coisa, show!
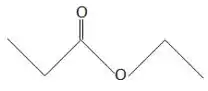
Passo 3
Na letra c a gente tem um ácido carboxílico e uma amina, o produto vai ser uma amida! E o número de carbonos a união dos dois, olha só como vai ficar:
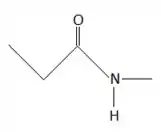
Passo 4
Na letra d a gente tem um ácido carboxílico e uma amina, também. Então segue o mesmo princípio do anterior:
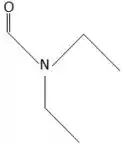
Show de bola! Conseguimos!
Resposta
-
; -
; -
; -
.