Estabilidade Nuclear
Produzido por Juliana EcheniqueTeoria
Eaii, tudo bem?
A gente já viu que alguns compostos químicos são radioativos, isso é: seus núcleos liberam diferentes partículas naturalmente e podem até se transformar em outros átomos (processo de transmutação).
As partículas mais comumente emitidas são:

O que a gente não sabe é prever como esses átomos radioativos vão se comportar. Isso é: se não nos disserem que o átomo emitiu 2 partículas , como a gente pode descobrir qual partícula ele vai emitir?
Razão nêutron-próton
Apesar de não existir nenhuma regra simples pra prever o decaimento nuclear dos átomos, existem algumas tendências que podem nos ajudar! O primeiro rolê que você tem que se ligar é a razão nêutron-próton.
Você lembra que os prótons são cargas positivas que se repelem mas que, no núcleo, essas forças de repulsão são estabilizadas pelos nêutrons, né? Nos átomos com poucos prótons, essa proporção costuma ser de 1:1, ou seja, para cada próton, a gente tem um nêutron.
Porém, conforme o número atômico vai subindo, a interação entre prótons fica cada vez maior e a gente precisa de cada vez mais nêutrons para compensar essa força de repulsão próton-próton e estabilizar o núcleo. Ou seja, a razão nêutron-próton aumenta, já que precisaremos de mais de um nêutron pra cada próton!
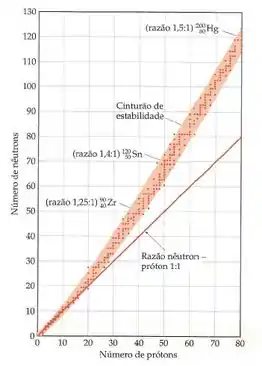
A gente pode então definir o cinturão (ou banda) de estabilidade. Dá uma olhada:
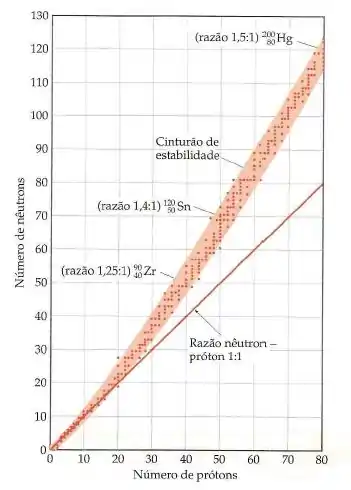
Esse cinturão representa todos os núcleos estáveis e ele termina em número atômico = 82 (o chumbo, Pb). A partir de , todos os elementos da tabela tem núcleo instável e são radioativos.
Mas como a gente usa o cinturão de estabilidade para prever o decaimento?
O mais importante aqui é entender que todos os decaimentos vão procurar deixar o núcleo o mais estável possível, isso é, vão tentar trazer o elemento para o cinturão de estabilidade! Vamos ver 3 casos possíveis:
1. Quando os núcleos estão acima do cinturão de estabilidade, isso é, tem altas razões nêutron-próton:
Como esses núcleos sofrem pelo excesso de nêutrons em relação aos prótons (são inclusive ditos ricos em nêutrons), eles vão ter tendência a emitir uma partícula ou até mesmo um nêutron! Isso porque a emissão da partícula diminui o número de nêutrons e aumenta o de prótons no núcleo filho:
![]()
2. Quando os núcleos tem baixas razões nêutron-próton, ou seja, estão abaixo do cinturão de estabilidade:
Esse tipo de núcleo é dito rico em prótons e tende a cair reduzindo o número de prótons, isso é, emitindo um pósitron, um próton ou capturando um elétron:
![]()
Assim, o número de prótons diminui e o número de nêutrons aumenta no núcleo filho.
3. Quando os núcleos tem mais de 82 prótons ():
Esse tipo de núcleo é instável e pesado e por isso tende a sofrer emissão alfa. A emissão de uma partícula diminui tanto o número atômico quanto o número de nêutrons no núcleo, o que facilita que esse núcleo chegue no cinturão de estabilidade!
Série de radioatividade
Existem alguns elementos radioativos que não ficam estáveis com só um decaimento. Por exemplo, quando o urânio-238 (emite uma partícula alfa, ele se transforma no tório-234 (, que ainda não é estável. Daí, ele tem que fazer sucessivas reações de decaimento até chegar em um núcleo estável (nesse caso, ele só para quando chega no chumbo-207, )!
Essas reações de decaimento sucessivas que começam com um núcleo instável e terminam com um núcleo estável se chamam série de reatividade!
Tem 2 macetinhos que nos ajudam a prever o tanto que um núcleo radioativo tem que decair para chegar na estabilidade. O primeiro macetinho é usar os números mágicos!
Mas que que isso quer dizer? Os números mágicos são números específicos de prótons e nêutrons que tornam um núcleo mais estável. Isso é, se o núcleo tem:
Ele tende a ser mais estável que núcleos que não tem esses números de prótons e nêutrons. Por exemplo, a partícula tem um núcleo duplamente mágico, com 2 prótons e 2 nêutrons.
Outro macetinho é você saber que núcleos de número par de prótons e nêutrons são mais estáveis!
Dá uma olhada nessa figura aqui embaixo pra perceber que quando a gente combina um número par de nêutrons e de prótons dá muito certo:
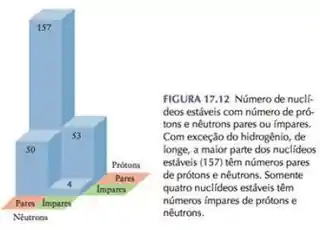
Repara também que a combinação número ímpar de nêutrons e número ímpar de prótons é o pior rolê possível!!
Muitas informações novas, né?
Vamos praticar um pouquinho pra fixar? 😊
Mas como a gente usa o cinturão de estabilidade para prever o decaimento?
Série de radioatividade
Exercícios Resolvidos
Exercício Resolvido #1
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, Exercício 17.13
Os seguintes nuclídeos estão fora da banda de estabilidade. Diga o tipo de decaimento preferencial de cada um deles, decaimento decaimento ou decaimento e identifique o núcleo filho:
a) cobre-68;
b) cádmio-103;
c) berquélio-243;
d) dúbnio-260.
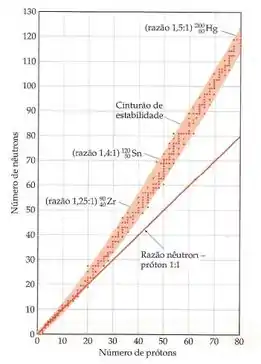
Utilize o gráfico abaixo para se basear:
Passo 1
Para saber qual o tipo preferencial dos decaimentos, a gente tem que analisar 2 coisas, nessa ordem:
- A gente tem que ver se o elemento tem mais de 82 prótons. Se ele tiver, ele vai ser instável e, para voltar para a banda de estabilidade, ele vai emitir partículas
- Se o elemento tiver menos de 82 prótons, a gente olha a razão nêutron-próton! Se a razão for alta, eles vão emitir partículas porque vão estar acima da banda de estabilidade. Se for baixa, vão emitir partículas porque vão estar abaixo da banda.
a) cobre-68, ou
Assim, a razão próton-nêutron vai ser:
Se a gente olhar no gráfico perto de 30 prótons, a gente vê que 1,34:1 como razão nêutron-próton é uma razão alta, porque o cobre-68 fica acima da banda de estabilidade. Outro jeito de pensar é usar o número de prótons e nêutrons para achar o composto no gráfico.
Dos dois jeitos, a gente vê que o cobre-68 vai emitir uma partícula !
A equação de decaimento vai ser:
Passo 2
b) cádmio-103, ou
O cádmio-103 tem e número de nêutros .
Sua razão nêutron-próton é, então:
A razão 1,14:1 é muiiito perto de 1 para a quantidade de prótons que o elemento tem. Podemos prever que ele vai ser pobre em nêutrons, e, olhando no gráfico, a gente confirma que ele tá abaixo da zona de estabilidade!
Assim, ele vai emitir uma partícula seguindo a equação:
Passo 3
c) berquélio-243 ou , tem , portanto, já podemos concluir que ele vai emitr partículas .
Passo 4
d) dúbnio-260 ou também tem o que indica que ele vai emitir partículas !
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 21.15
Um dos nuclídeos em cada um dos seguintes pares é radioativo. Determine qual é estável:
a) e ;
b) e
c) magnésio-25 e neônio-24.
Justifique sua resposta.
Dados:
Passo 1
a) Para comparar a estabilidade dos dois isótopos do potássio, vamos começar calculando o número de nêutrons de cada um:
Como 20 é um número mágico, a gente pode concluir direto que o vai ser mais estável!
Passo 2
b) O bismuto tem . O número de nêutrons de seus isótopos, então, vai ser:
Como o primeiro isótopo tem um número mágico de nêutrons, ele vai ser mais estável!
Passo 3
c) magnésio-25 (ou ) e neônio-24 (ou ).
Vamos começar calculando o número de nêutrons de cada um!
Nenhum dos dois tem número de nêutrons nem de prótons mágico, então vamos ter que apelar para a razão nêutron-próton!
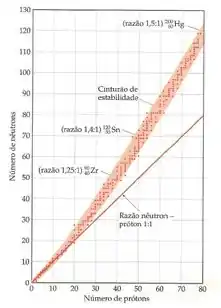
Se a gente olha o gráfico, a gente consegue ver que os dois estão em uma região onde a banda de estabilidade está com a razão 1:1, né? Mas os dois estão acima da banda de estabilidade! A questão é saber quem tá mais longe, ou seja, quem tem a maior razão nêutron-próton!
Ou sejaaa, o tem uma razão nêutron-próton maior que o Mg, o que o afasta mais da banda de estabilidade e indica que ele é o mais instável!
O é o composto estável.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Lista de exercícios UFPB – Prof. Ary da Silva Maia
Os pares abaixo são formados por um nuclídeo estável e um radioativo. Indique o radioativo e explique sua escolha.
- 51Sb122 ; 54Xe136
- 82Pb204 ; 85At204
- 37Rb87 ; 37Rb80
Passo 1
a) Vamos começar analisando se algum deles tem número mágico de nêutrons (já que não tem de prótons).
Yeyy! Como o Xe tem um número mágico de nêutrons, já conseguimos concluir que ele é o estável.
Passo 2
b) Nesse caso, nem precisaríamos analisar o número de nêutrons, já que o chumbo tem um número de prótons mágico! O que indica que ele é o nuclídeo estável. Maaaas, como o outro pode ter número mágico de nêutrons, não custa nada dar uma conferida:
Tudo certo, o chumbo é mesmo o nuclídeo estável.
Passo 3
c) Calculando o número de nêutrons...
Como o primeiro isótopo do Rb tem número de nêutrons mágico, é o isotopo estável!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 21.16
Em cada um dos seguintes pares, qual nuclídeo você esperaria ser o mais abundante na natureza:
a) ;
b);
c) paládio-106 ou paládio-113;
d) xenônio-128 ou césio-128?
Justifique.
Passo 1
Para analisar a abundância na natureza, a gente tem que ver se o número de prótons e o número de nêutrons são pares. A combinação em que os dois números são pares estabiliza o elemento e aumenta a probabilidade de que ele seja encontrado na natureza.
Se um dos dois for ímpar e o outro for par, ainda é melhor do que a combinação ímpar-ímpar, a mais instável de todas.
a) Calculando o número de nêutrons...
Como no isótopo de massa 112 o número de nêutrons é par, ele vai ser o mais estável e, consequentemente, mais abundante na natureza!
Observação: a gente pode ou calcular o número de nêutrons ou simplesmente olhar o número de prótons e de massa. Como a massa é a soma de prótons + nêutrons, se o número de prótons é par e o de massa também, isso significa que o número de nêutrons também vai ser 😊
Passo 2
b) Nesse caso, como o número de prótons é ímpar, a gente tem que ver se algum deles tem o número de nêutrons par!
Como o alumínio-27 tem número de nêutrons par, ele vai ser mais estável que o alumínio-30 e vai ser mais abundante na natureza!
Passo 3
c) paládio-106 ou paládio-113
O paládio tem , um número par. Assim, o paládio-106 vai ser mais estável, já que ele vai ter número de prótons par também! (já que o número de massa é par e é formado por prótons+nêutrons 😊)
Passo 4
d) xenônio-128 ou césio-128
Nesse caso, a gente tem que olhar o número de prótons, já que os dois tem número de massa par. O xenônio tem e o césio, . Por isso, o xenônio vai ter a dobradinha número de prótons e nêutrons par, e vai ser mais estável e mais abundante na natureza que o césio.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 21.18
O estanho-112 é um nuclídeo estável, mas o índio-112 é radioativo, com uma meia-vida de apenas 14 min. Como podemos explicar essa diferença na estabilidade nuclear?
Passo 1
Antes de mais nada, vamos olhar os números de nêutrons e de prótons dos dois, já que, se um dos dois números for um número mágico, o nuclídeo é estável.
O estanho tem e o índio, .
Já podemos ver que o estanho tem um número mágico de prótons, o que explica porque ele é mais estável que o índio.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Lista de exercícios UFPB – Prof. Ary da Silva Maia
Diga o tipo de decaimento radioativo esperado para cada nuclídeo:
- 92U238b) 5B8c) 29Cu68
Passo 1
a) Como o isótopo do urânio tem mais de 82 prótons, podemos prever que, para que ele volte para o cinturão de estabilidade, ele vá emitir partículas alfa!
Passo 2
b) Esse isótopo do Boro, se a gente olhar no gráfico, tem uma razão nêutron-próton muito baixa, o que significa que ele vai ficar abaixo do cinturão de estabilidade. Por isso, esse isótopo vai emitir uma partícula ou até mesmo um próton.
Passo 3
c) Com o número de nêutrons , a gente pode ver no gráfico que esse isótopo está acima do cinturão de estabilidade, o que significa que ele está rico em nêutrons. Por isso, ele vai emitir ou uma partícula beta ou um nêutron.
Resposta
Ei, a resposta está no passo a passo :)