Energia Livre de Gibbs
Teoria
A espontaneidade de um processo qualquer depende de um balanço entre a variação de energia e a variação de entropia. A Energia Livre de Gibbs (ΔG) é uma grandeza que nos permite fazer esse balanço e prever se uma reação vai ser espontânea ou não.
Quando o for negativo o processo se dá de forma espontânea e quando for positivo a reação é não espontânea.
E temos que dar aquela relembrada em Entropia (ΔS) e na Entalpia (ΔH), a primeira mede a quantidade de desordem do nosso sistema, e a segunda que tem tudo a ver com o calor envolvido na reação!
Sendo assim podemos analisar também a espontaneidade em função de cada termo, é isso que veremos nessa tabelinha aí em baixo. Nela mostramos as reações que serão sempre espontâneas, as que vão ser dependentes da temperatura e as que vão ser sempre não espontâneas.
Para os processos em que é a espontaneidade depende da temperatura, basta analisar a equação de Gibbs como uma função do primeiro grau, mas para isso vamos precisar saber os valores de ΔH e de ΔS.
Que para visualizar melhor poderia ser visto como essas opções de gráficos aqui:
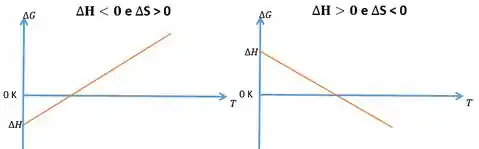
Bem, isso faz bastante sentido com o nosso exemplo do gelo, afinal o gelo derreteu quando exposto a uma temperatura alta. Se fossemos colocar o gelo sobre a mesa na Sibéria, numa temperatura bem menor, certamente o gelo não derreteria.
Uma coisa muito importante é que a análise feita aqui só mostra se um processo vai acontecer ou não, agora se isso vai ser rápido ou demorado é outra coisa. O diamante por exemplo é uma forma de carbono que espontaneamente se transformará em grafite, só que isso levará milhões de anos para ocorrer.
Outra informação importante sobre o é que ele representa a quantidade máxima de energia, elétrica ou mecânica, que está disponível para ser transformada em trabalho quando uma reação ocorre a temperatura e pressão constante. O trabalho obtido por qualquer reação química em um dado processo real será sempre menor que o valor de , isso se dá por que os processos reais são sempre irreversíveis, e o trabalho máximo só pode ser extraído de um processo reversível.
Então a eficiência de um processo está relacionada com o ! E isso é muito importante por que mesmo os processos mais eficazes, que são os biológicos, aproveitam em média 40% de toda a energia que estaria disponível. Já nas máquinas é comum aproveitamentos inferiores a 30% e vale lembrar que qualquer aumento nessa porcentagem aí já significa uma grande economia.
Agora o que falta é cair dentro da lista de exercícios para mandar bem na prova, então vamos lá!!! :D
Exercícios Resolvidos
Exercício Resolvido #1
Lista de termodinâmica - Universidade de São Paulo
Se para uma reação a todas as temperaturas, então é ______ e é ______.
- positivo, positivo
- positivo, negativo
- zero, positivo
- negativo, positivo
- negativo, zero
Passo 1
Vamos de questãozinha teórica para fortalecer nossos conhecimentos! 
A questão nos dá opções para completar a frase aí de cima. E o que isso quer dizer, quais serão os sinais da variação de entalpia (ΔH) e variação de entropia (ΔS) para que a variação de energia livre de Gibbs (ΔG) seja negativo, independente do valor da temperatura...Hum...
Sabe o que pode nos ajudar nisso?
Aquela tabelinha de sinais que vimos na teoria! Vamos relembrá-la no próximo passo!
Passo 2
Essa tabelinha nos mostra quais os sinais de ΔH e de ΔS para o ΔG, ser espontâneo, ou seja negativo! Vamos olhar com calma:
Passo 3
Opa! Já encontramos nossa resposta, hein?
A tabela diz que para e o nosso ΔG é sempre espontâneo, então é sempre negativo!
Uhul! Já foi! Encontramos nossa resposta!
Resposta
Letra b.
Exercício Resolvido #2
Adaptado de James E. Brady e Gerard E. Humiston Volume 1, 2ª edição: Livros Técnico Científicos Editora. Página 448 exercício 11.28
Quais os critérios devem ser satisfeitos para que um processo seja espontâneo independentemente da temperatura?
Passo 1
A esponteneidade de processos pode ser verificada pela Energia Livre de Gibbs, , de modo que quando , temos que o processo é espontâneo. Então precisamos ver a fórmula dessa tal Energia Livre de Gibbs e ver como ela pode ser sempre negativa, sem precisar depender da temperatura.
Logo, para que seja sempre negativo, é preciso ter e um . Sendo assim, seja qual for a temperatura, a equação acima vai apresentar valores de sempre negativos.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Adaptado de James E. Brady e Gerard E. Humiston Volume 1, 2ª edição: Livros Técnico Científicos Editora. Página 448 exercício 11.31
Por que é possível uma reação química ocorrer espontâneamente, ainda que o
para a reação seja positivo?
Passo 1
O de uma reação é chamado “Energia Livre de Gibbs Padrão” (tá vendo aquela bolinha ali? Pois é!).
Ele calculado a uma temperatura padrão, que no caso é , ou . Então, esse valor serve apenas para determinar se uma reação é espontânea nessa temperatura. Já o cálculo de Energia Livre de Gibbs pode ser estendido a outras temperaturas e comprovar a espontaneidade da reação química para uma situação particular.
Passo 2
Então é possível que uma reação tenha positivo, mas negativo, e seja espontânea a uma determinada temperatura.
Caso a reação tenha entalpia e entropia negativas, ela poderá se tornar espontânea caso esteja em baixas temperaturas. Por outro lado se tanto a entalpia quanto a entropia forem positivas o processo pode não ser espontâneo na temperatura padrão e passar a ser a temperaturas mais elevadas.
Vale elmbrar que caso a entalpia seja negativa e a entropia positiva a reação é sempre espontânea e que, por outro lado, caso a entalpia seja positiva e a entropia negativa o processo é não espontâneo para qualquer temperatura.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração prórpia.
A amônia é uma molécula formada por nitrogênio e hidrogênio sendo a sua síntese um importante passo para o desenvolvimento de fertilizantes e, consequentemente, para a existência da civilização como hoje a conhecemos. O processo usado para sua produção foi desenvolvido por Fritz Haber e Carl Bosch em 1909. A reação que forma a amônia se dá entre o gás nitrogênio e o gás hidrogênio na presença de um catalisador a temperaturas geralmente entre e .
Haber foi laureado com o prêmio Nobel por esse trabalho em 1918. Contudo, a sua premiação
causou uma série de protestos, pois, durante a 1º Guerra Mundial, ele ficou conhecido como o “pai da guerra química”, tendo desenvolvido alguns gases usados nos conflitos. Há registros de abril de 1915 onde mais de 5 mil homens morreram devido a inalação de gás cloro, fora outros 10 mil que apresentaram graves sintomas de intoxicação. A obtenção indistrial da amônia é usualmente feita pelo processo conhecido como “processo Harbber-Bosch”.
- Calcule de formação da amônia a 298 K a partir dos valores de H e S dados abaixo. A reação será espontânea?
- No processo mencionado, a reação se dá a temperaturas superiores a Indique se esta temperatura elevada seria um fator importante para a espontaneidade do processo.
Dados:
Passo 1
O cálculo da Energia Livre de Gibbs é feito usando a seguinte fórmula:
Então vamos começar pelo cálculo da variação de entropia, , da reação.
Repara que a unidade ficou J/K, porque multiplicamos os valores dados por número de mols.
Agora seguindo com os cálculos de .
Atenção para a unidade da entalpia que está em kJ, não vai vacilar nisso né? E já que resolvi chamar atenção para os erros mais comuns, se liga aí e não esquece de multiplicar a entalpia por já que na reação há a formação de unidades de amônia. Dito isso vamos aos cálculos.
Que pode ser aproximado para:
Então temos que essa reação é espontâna já que o valor da energia livre de Gibbs deu negativo.
“Ah, mas por que a gente calculou e pro só pegamos os valores do produto?”
Porque os reagentes estão na forma alotrópica mais estável deles, então o de formação deles seria zero.
Valeu?
Passo 2
Item b agora! Olha aí nossa energia livre de Gibbs:
Até aqui nada de novo. Mas vamos analisar isso aí:
Como usamos em Kelvin, Portanto, o termo e quanto maior for o valor de , maior será o valor de . Conclusão: a elevação da temperatura nessa reação não favorece a sua espontaneidade.
“Mas se o aumento da temperatura não favorece a espontaneidade, porque os caras aumentam a temperatura”?
Na vida há duas coisas: a espontaneidade e a velocidade. Ou: a termodinâmica e a cinética. Lembra que a gente comentou que alguns processos são espontâneos mas podem levar milhares de anos pra ocorrer? Ou seja, eles são espontâneos, mas muito lentos... Tem cinética muito baixa. E como que faz pra aumentar a cinética? Aumenta a temperatura!! Porque aí aumenta o número de choques efetivos e tal.
Não to dizendo que a reação de formação da amônia levaria milhares de anos para ocorrer, mas ainda assim o aumento de temperatura melhora o fator cinético, ainda que prejudique o fator termodinâmico.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração prórpia.
Determine tendo a seguinte reação química:
Para tal, utilize a relação matemática de energia livre de Gibbs, e ;
Dados:
Passo 1
A primeira coisa que eu espero que tenha chamado a sua atenção nesse exercício é que existem mais dados do que vamos precisar. Ali entre as informações tem os valores das entalpias e das entropias para a água gasosa e também para a água líquida, mas de fato vamos usar apenas um desses para nossos cálculos. Como a reação mostrada leva à formação da água líquida, então usaremos os dados referentes à água nesse estado físico.
O cálculo da energia livre de Gibbs é feito usando a seguinte fórmula:
Então vamos começar pelo cálculo da variação de entropia, , da reação.
E agora entalpia:
Mas aí ferrou, não temos a entalpia dos reagentes!!!!
Calma aííí. Basta lembrar que a entalpia de uma substância em seu estado alotrópico mais estável é 0! Falei grego?
Quando a susbtância tá no seu estado mais simples, a entropia dela é zero.
Existe alguma molécula contendo hidrogênio que seja mais simples que o ? Não né... então a entalpia do é zero! E pro oxigênio? A molécula mais simples contendo oxigênio é o , então esse cara tem entalpia zero também!
Então:
Agora seguindo com os cálculos de :
Passo 2
Bem, não podemos esquecer que a questão quer que calculemos o , ou seja, após ter feito aquilo tudo temos que dividir o valor obtido afim de determinar a variação de energia livre de Gibbs para cada mol de água líquida que é formada. Então bora fechar essa questão logo:
Ou, aproximando o resultado:
Resposta