Modelos mecânicos
Produzido por Alexandre NunesTeoria
Introdução
E ai galera! Tudo tranquilo?
Agora estamos naquele momento em que muitas vezes temos um sistema real físico, como por exemplo um carro numa estrada e precisamos modelar o sistema de amortecimento dele.
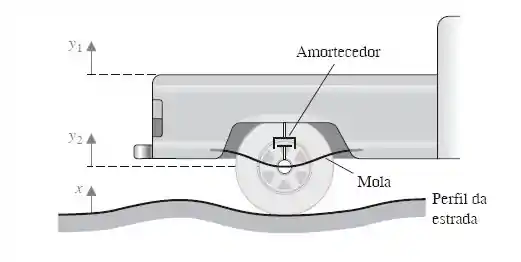
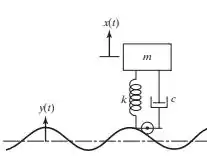
Esse sistema podem ser modelado das mais diversas formas, umas mais simples e outras mais complexas, isso vai depender do que precisamos avaliar e por consequência das hipóteses que vamos adotar. Como por exemplo, o sistema carro andando na estrada pode ser modelado com um grau de liberdade.
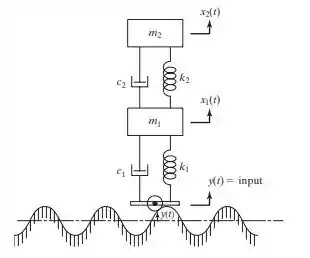
Com dois graus de liberdade.
Esse nível de detalhe vai depender da nossa necessidade, para nossa sorte, já foi observado que os graus de liberdade podem variar, mas existem elementos primários que aparecem representando características do sistema, que são: inércia, amortecimento e rigidez.
Além desses elementos primários, quando o sistema é de segunda ordem, o que ocorre normalmente, pois é o elemento primário de inércia que ocasiona isso, podemos relacionar esses para termos mais dois novos parâmetros: critério de amortecimento e frequência natural.
Agora vamos lá entender como eles estão relacionados.
Equação do movimento
Em sistemas mecânicos, conseguimos associar um sistema real com um sistema massa-mola-amortecedor, cada uma dessas forças são conhecidas como elementos primários, que podem ser de translação ou de rotação.
Para conseguir a correlação dessas forças usamos a segunda lei de Newton.
Como trabalhamos com sistemas invariantes no tempo, a massa () não varia. Se ela variasse, caso do foguete, não poderíamos utilizar a transformada de Laplace e por consequência não teríamos uma função de transferência e sem ela, nada de controle clássico.
Sendo sendo a força , a massa e o deslocamento linear .
Caso o sistema seja rotacional, não tem problema, só alterar os termos relacionados a translação pelos seus equivalentes relacionados a rotação, repaginando então a segunda lei de Newton:
Sendo sendo o torque, o momento de inércia e o deslocamento angular .
Elementos primários de translação
Os três tipos de força encontrados ao realizarmos nossa modelagem podem ser consideradas dentro desses três tipos
Sendo a massa , o deslocamento linear , a velocidade .
Sendo a constante elástica , o deslocamento linear , a velocidade .
Em sistemas mecânicos de translação, a restituição é normalmente caracterizada por uma mola. Vale lembrar quando se trata de molas que elas podem ser arranjadas em paralelo (a) e em série (b).
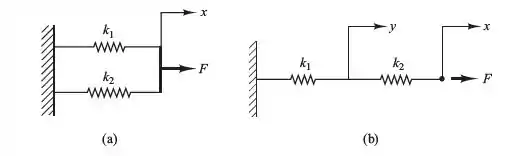
E isso resulta num com a seguinte relação:
Sendo o coeficiente de atrito viscoso , o deslocamento linear , a velocidade .
Essa relação acima ocorre, pois admitimos que o amortecimento é linear. E o amortecimento representa as forças dissipativas do nosso sistema, ou seja, as que diminuem a energia armazenada no sistema.
Assim como as molas, é possível arranjar os amortecimentos em paralelo (a) e em série (b)
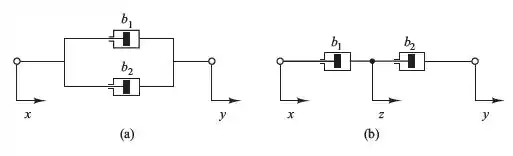
E eles tem um da seguinte forma:
Elementos primários de rotação
Apresentados os elementos primários de translação, os de rotação são idênticos com a alteração dos termos relacionados com a translação para termos relacionados com rotação, ou seja, o torque substitui a força e o deslocamento angular substitui o deslocamento translacional.
Sendo o momento de inércia , o deslocamento angular , a velocidade .
Sendo a constante de mola torcional , o deslocamento angular , a velocidade .
A relação para molas torcionais em série e paralelo são as mesmas do sistema de translação.
Sendo o coeficiente de atrito viscoso , o deslocamento angular , a velocidade .
A relação para molas torcionais em série e paralelo são as mesmas do sistema de translação.
Equação do movimento
Elementos primários de translação
Elementos primários de rotação
Exercícios Resolvidos
Exercício Resolvido #1
Prof. Heraldo L. S. Almeida – Modelagem matemática de sistemas físicos – Escola politécnica UFRJ – Exercício 4.22
Para o sistema mecânico da figura abaixo, sendo , o sinal de entrada e , o sinal de saída, obter a função de transferência do sistema.
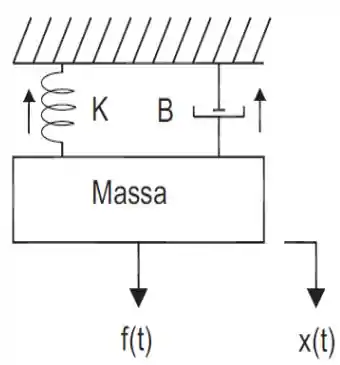
Passo 1
Para esse exercício, precisaremos obter uma relação de equilíbrio entre as diferentes forças envolvidas.
Temos três forças agindo sobre o nosso objeto: a força , a força da mola e a força de atrito.
A força da mola será:
E a força de atrito:
Passo 2
Vamos arbitrar que a força é positiva para baixo e negativa para cima. Sendo assim:
A força resultante sobre o corpo, pode ser escrita usando-se a Segunda Lei de Newton:
Sendo a aceleração do corpor, e aceleração é a derivada dupla da posição. Substituindo na equação de equilíbrio:
Passo 3
Como o exercício pede a função de transferência do sistema, precisamos tirar a transformada de Laplace da equação acima e encontrar a relação entre a força e a posição .
Aplicando Laplace:
Essa parte da transformada de Laplace é bem importante, se você estiver com dúvidas nesse passo seria legal dar uma revisada no tópico de transformadas de Laplace.
Rearrajando:
Logo:
Resposta
Exercício Resolvido #2
Prof. Heraldo L. S. Almeida – Modelagem matemática de sistemas físicos – Escola politécnica UFRJ – Exercício 4.23
Escreva as equações de movimento para a velocidade do carro conforme mostrado na figura abaixo assumindo que o motor fornece uma força . Obetnha a transformada de Laplace da equação diferencial resultante e encontre a função de transferência entre a entrada e a saída .
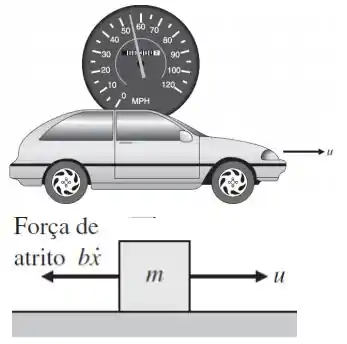
Passo 1
Precisamos encontrar a relação entre a força que o motor aplica no carro e a sua velocidade.
Nesse caso, precisamos considerar duas forças agindo sobre o carro, a força fornececida pelo motor e a força de atrito.
Usando a segunda lei de newton:
Sendo a aceleração do corpo, e aceleração é a derivada dupla da posição. Substituindo na equação de equilíbrio:
Passo 2
Por enquanto, temos uma EDO que relaciona a força fornecida pelo motor com a posição do carro, entretanto, precisamos encontrar a relação com a velocidade e não com a posição. Como a velocidade é a derivada da posição, podemos usar essa relação:
Logo:
Rearranjando:
Passo 3
Obtivemos então a EDO que relaciona a velocidade do carro com a força fornecida pelo motor:
O próximo passo agora é aplicar a transformada de Laplace:
Essa parte da transformada de Laplace é bem importante, se você estiver com dúvidas nesse passo seria legal dar uma revisada no tópico de transformadas de Laplace.
Rearrajando:
Logo:
Resposta
Exercício Resolvido #3
Prof. Heraldo L. S. Almeida – Modelagem matemática de sistemas físicos – Escola politécnica UFRJ – Exercício 4.27. Adaptado.
Determine a amplitude e a frequência de oscilação da resposta a um impulso de torque no pêndulo de torção sem atrito representado abaixo, composto de um corpo rígido de inércia rotacional 𝐽 suspenso por um fio com rigidez rotacional 𝐾.
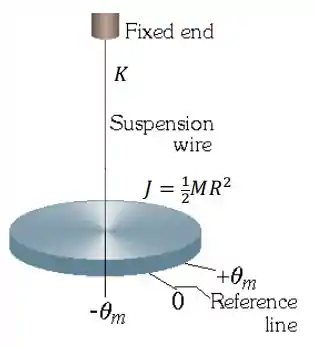
Passo 1
Nesse exercício temos um sistema mecânico rotacional.
Precisamos encontrar uma expressão para o ângulo de rotação , para isso, vmos escrever a equação de equilíbrio de torque:
O torque resultante é a soma de todos os torques, e temos que:
Logo:
Nesse caso, não temos atrito, mas temos um impulso de torque, , e também temos um fio com rigidez rotacional, , que atrapalha a rotação.
Passo 2
Devemos agora aplicar transformada de Laplace na nossa EDO:
Essa parte da transformada de Laplace é bem importante, se você estiver com dúvidas nesse passo seria legal dar uma revisada no tópico de transformadas de Laplace.
A transformada de Laplace da função de torque foi devido ao fato de ser uma função impulso. Funções impulso sempre vão ter transformada de Laplace igual a 1.
Rearranjando:
Passo 3
Já obtivemos a expressão para o ângulo no domínio :
Se manipularmos um pouco teremos:
Fizemod essa manipulação para conseguir aplicar a inversa da transformada de Laplace. Se olharmos uma tabela com transformadas de Laplace, veremos que essa função ficou com o mesmo formato da transformada da função seno. Fazedno a transformada inversa teremos:
Passo 4
O exercício pede a amplitude e frequência de oscilação.
A amplitude é a constante que multiplica a função seno:
E a frequência é o argumento da função:
Resposta
Exercício Resolvido #4
Prof. Amintas Paiva Afonso – Intodução aos sistemas dinâmicos – 4 – Sistemas de controle
Encontre a função de transferência do sistema de massa molo abaixo:
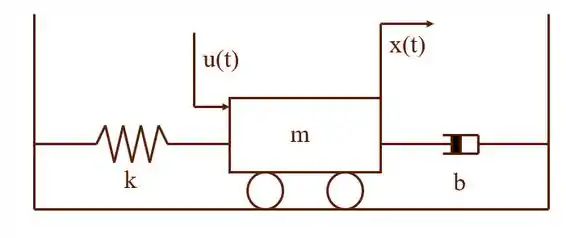
Passo 1
Aqui nessa questão temos um corpor e três forças agindo sobre ele: a força , a força da mola e a força proveniente do sistema de amortecimento. Sendo assim:
Usando a segunda lei de newton:
Sendo a massa do corpo e a aceleração.
Aceleração é a derivada dupla da posição. Substituindo na equação de equilíbrio:
Passo 2
Vamos rearranjar para deixar tudo que tem a a posição do lado esquerdo da equação:
Já temos a nossa EDO no jeitinho. O próximo passo é aplicar a transformada de Laplace nela para que possamos determinar a função de transferência:
Aplicando Laplace:
Só lembrando: se você não está se lembrando como fazer esse passo, seria legal dar uma revisa em transformadas de Laplace. Esse passo é fundamental e precisa estar na ponta da língua hein.
Passo 3
Colocando em evidência do lado esquerdo da equação:
Rearranjando:
Resposta
Exercício Resolvido #5
Elaboração própria
Encontre as funções de transferência e do sistema abaixo:
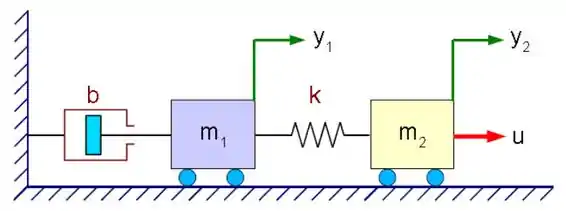
Passo 1
Vamos escrever a equação de equilíbrio de forças para cada um dos corpos.
Para o bloco 1:
O primeiro sofre influência da força de amortecimento e da força da mola.
Para o bloco 2:
O segundo bloco sente o efeito apenas da força da mola e da força
Vamos rearranjar essas expressões para ficar melhor para a gente trabalhar:
Passo 2
As EDOs já estão no jeito. Vamos aplicar Laplace nelas então:
Só lembrando: se você não está se lembrando como fazer esse passo, seria legal dar uma revisa em transformadas de Laplace. Esse passo é fundamental e precisa estar na ponta da língua hein.
Passo 3
Vamos isolar em e substituir em :
Substituindo:
Rearranjando:
Por fim:
Substituindo em :
Resposta
Exercício Resolvido #6
Prof. Heraldo L. S. Almeida – Modelagem matemática de sistemas físicos – Escola politécnica UFRJ – Exercício 4.26
Encontre as função de transferência para o sistema mecânico abaixo:
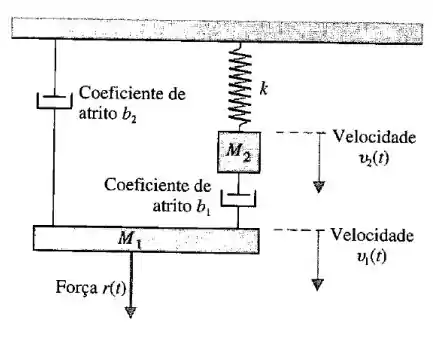
Passo 1
Vamos começar escrevendo a equação de equilíbrio para o bloco 1:
Como queremos uma expressão que relacione a velocidade com a força :
Rearranjando:
Analogamente para o segundo bloco teremos:
Fazendo:
E, consequentemente:
Rearranjando:
Passo 2
Agora que já fizemos a modelagem do sistema mecânico, devemos aplicar a transformada de Laplace nas expressões (1) e (2).
Para a expressão (1):
Rearranjando:
Aplicando Laplace na expressão (2):
Passo 3
Para terminar, vamos isolar em (4) e substituir em (3):
Substituindo em (3):
Logo:
Por fim:
Resposta
Exercício Resolvido #7
Prof. Heraldo L. S. Almeida – Modelagem matemática de sistemas físicos – Escola politécnica UFRJ – Exercício 4.25
Encontre as funções de transferência e para o sistema mecânico abaixo:
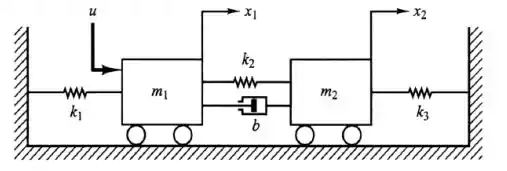
Passo 1
Precisamos então encontrar a função de transferência que relaciona a posição de cada um dos blocos com a força aplicada.
Para o primeiro bloco teremos:
A força resultante ( é igual a soma de todas as forças atuantes no bloco. Para o primeiro bloco temos a força de entrada , a força proveniente das molas 1 e 2 e a força de atrito.
Analogamente para o segundo bloco teremos:
Vamos tentar reorganizar essas equações para conseguir trabalhar com elas um pouco mais facilmente. Para a primeira equação, vamos deixar tudo que tem do lado direito e todo o resto do lado esquerdo:
Para a segunda equação, vamos deixar tudo que tem do lado esquerdo:
Passo 2
Obtivemos então as EDOs que regem o sistema:
O próximo passo agora é aplicar a transformada de Laplace. Para a primeira equação:
E para a segunda:
Rearranjando as equações obtidas:
Passo 3
Para achar as expressões de e precisaremos fazer um pouco de algebrismo. Vamos então isolar na equação (2):
Substituindo na equação (1), teremos:
Rearranjando:
Finalmente:
Já achamos , agora só falta .
Substituindo a equação para que acabamos de encontrar, na equação (2):
Podemos cancelar o termo que aparece dos dois lados da equação:
Finalmente:
Resposta
Exercício Resolvido #8
Prof. Heraldo L. S. Almeida – Modelagem matemática de sistemas físicos – Escola politécnica UFRJ – Exercício 4.30. Adaptado.
Obtenha a função de transferência, que representa o sistema mecânico abaixo:
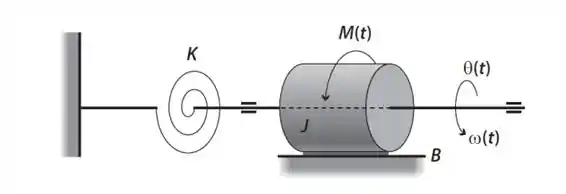
Passo 1
Nesse exercício temos um sistema mecânico rotacional.
O torque resultante é a soma de todos os torques, e temos que:
Logo:
Nesse caso temos um momento angular , mas também temos um momento de atrito e de resistência do fio que “atrapalham” a rotação:
Passo 2
Para achar a função de transferência agora só precisamos aplicar a transformada de Laplace e depois manipular a equação obtida. Aplicando Laplace:
Rarranjando: