Série de Taylor e Linearização
Teoria
Fala aí! Hoje vamos falar um pouquinho sobre Série de Taylor e como usamos isso para linearizar funções!
⭐ Veja também ⭐
Série de Taylor
A série de Taylor é uma série de funções usada para aproximar uma função em torno de um ponto de interesse.
Ela tem essa carinha bonitinha aqui:
E o que são esse tanto de letras que apareceram aí?
👉
👉
Muita informação? Tudo isso eu te explico com um pouquinho mais de detalhes aqui. Por enquanto, vamos focar em como usamos isso aí para linearizar uma função.
Ah, se você preferir, confere esse vídeo aqui explicando tudo isso que eu tô te contando. Se não, continua comigo logo abaixo no textinho 🥰
Linearização
A linearização é o nome que damos ao processo de transformar uma curva qualquer em uma reta.
Representação Gráfica
Graficamente, o que vamos fazer é isso aqui:
Para um gráfico não linear
A reta tangente em um ponto central (dada pela derivada) terá valores muito próximos aos da função original, em regiões perto desse ponto.
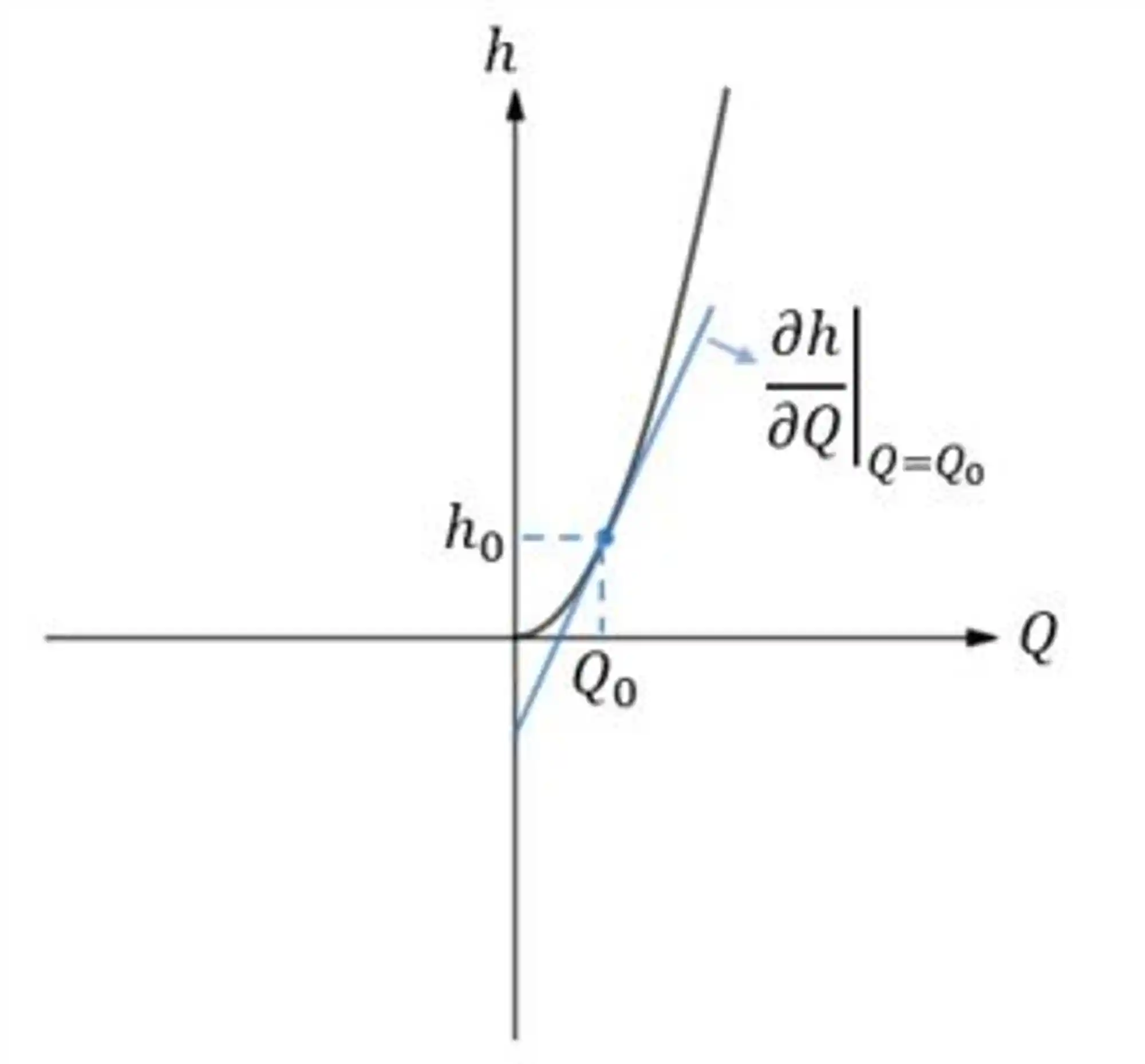
Percebe como as curvas estão bem próximas ali perto daquele ponto
Se quisermos olhar para outro ponto, temos que fazer uma nova linearização em torno desse novo ponto. beleza?
Então, bora ver, finalmente, como fazemos esse negócio aí.
Expansão em Série de Taylor
Para fazer a expansão em série de Taylor, vamos abrir aquele somatório mostrado lá no começo.
Mas é claro que você não vai repetir isso aí infinitas vezes, né? Na grande maioria dos casos, vamos desconsiderar todos os termos além da primeira ordem.
Então só vamos trabalhar com isso aqui:
No exemplo daquela função lá do gráfico, tínhamos a função da perda de carga numa válvula. Dada por:
Se quisermos linearizar essa função em torno de uma vazão
Como
E a expansão vai ficar assim:
Agora, podemos reorganizar isso aí.
Olha só,
Pra ficar mais bonitinho, vamos substituir o seguinte:
Então:
Tá aí, nossa equação linearizada 🥰
Linearização
Expansão em Série de Taylor
Exercícios Resolvidos
Exercício Resolvido #1
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 2.26
Linearize em torno de
Passo 1
O primeiro passo é identificar em que ponto vamos fazer a nossa linearização. O enunciado do exercício já define para nós que ponto é esse:
Portanto devemos aplicar a fórmula da linearização de Taylor abaixo:
Passo 2
Vamos fazer termo a termo.
Substituindo na fórmula:
Passo 3
Agora devemos substituir por
Como:
e
Resposta
Exercício Resolvido #2
Elaboração própria
Linearize em torno de
Passo 1
Relembrando a fórmula da linearização de Taylor:
Nesse caso o ponto fixo nos foi dado. Portanto:
Passo 2
Fazendo termo a termo:
Substituindo:
Passo 3
Substituindo então por
Tirando o do denominador pra ficar mais bonitinho:
Resposta
Exercício Resolvido #3
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 2.27
Linearize a equação em torno de
Passo 1
O termo não linar da equação é o e é com ele que trabalharemos. Sendo assim:
Para linearizar, utilizaremos como sempre a linearização de Taylor:
Passo 2
Vamos fazer termo a termo.
Substituindo na fórmula:
Passo 3
Agora devemos substituir por
Como:
e
Passo 4
Para finalizar, basta substituir a função encontrada na equação inicial:
Resposta
Exercício Resolvido #4
Prof. Ninoska Bojorge, UFF, Lista 1 2019.1. Adaptado
Linearize a equação:
Passo 1
Devemos encontrar a parte da nossa equação que não é linear.
Nesse caso, toda parte à esquerda na equação não é linear devido aos termos elevado ao cubo e ao quadrado.
Para linearizar, seguiremos com a linearização de Taylor:
Passo 2
Fazendo termo a termo.
Substituindo na fórmula:
Passo 3
Como o enunciado não fornece o ponto da linearização, deixaremos tudo em função de .
Para finalizar, basta substituir a função encontrada na equação inicial:
Resposta
Exercício Resolvido #5
Elaboração própria
Linearize a equação:
Passo 1
Para linearizar a equação, precisaremos primeiro identificar o termo não linear. Na EDO do exercício o único termo não linar é a raiz quadrada, sendo assim:
Para linearizar, seguiremos com a linearização de Taylor:
Passo 2
Para facilitar, e não correr risco de errarmos, vamos fazer termo a termo:
Substituindo na fórmula:
Passo 3
Como o enunciado não fornece o ponto da linearização, deixaremos tudo em função de .
Para finalizar, basta substituir a função encontrada na equação inicial:
Resposta
Exercício Resolvido #6
Elaboração própria
Linearize a equação:
Passo 1
Além de termos elevados a expoentes que são diferentes de , outra situação que causa a não-linearidade de uma função é a multiplicação de duas ou mais funções. Nesses casos, nós ainda usaremos a linearização de Taylor, mas ela vai sofrer uma leve alteração:
A lógica continua a mesma: primeiro a gente escreve a função em torno do ponto onde estamos linearizando, depois nós vamos derivar a função duas vezes, uma vez em relação a cada função que compõe a função principal. Bora lá?
Passo 2
Vamo fazer passo a passo pra não errar:
Substituindo na linearização:
Resposta
Exercício Resolvido #7
Elaboração própria
Linearize em torno de
Passo 1
Relembrando a fórmula da linearização de Taylor:
Nesse caso, o ponto fixo nos foi dado, portanto:
Passo 2
Fazendo termo a termo:
Substituindo:
Passo 3
Substituindo então por
Resposta
Exercício Resolvido #8
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 47, Exemplo 2-6.1. Adaptado
Faça a linearização da equação de Arrheinus para a dependência da temperatira dos coeficientes de velocidade das reações químicas em torno de . Considere , e uma energia de ativação de .
Passo 1
Relembrando a fórmula da linearização de Taylor:
Devemos linearizar em torno do ponto
Passo 2
Fazendo termo a termo:
Repare que o primeiro termo da equação da derivada, é idêntico à expressão de
Sendo assim:
Substituindo na linearização:
Passo 3
Sunstituindo os valores: