Controle cascata
Produzido por Alexandre NunesTeoria
Introdução
O controle feedback é o mais comum e o mais usado na indústria, isso é notícia velha já. Entretanto, nem todo processo que a gente vai encontrar por aí o feedback vai dar conta de controlar adequadamente. Por isso é necessário criar estratégias mais elaboradas de controle para atender a esses processos mais rigorosos.
Uma delas é o controle feedforward, que é aquele que mede um distúrbio para tentar controlar o processo antes mesmo desse distúrbio impactar o processo, lembra?
E uma outra opção é o controle representado pelo diagrama de blocos da figura abaixo:
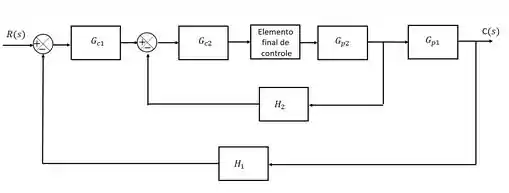
Esse cara aí é, nada mais nada menos, que o sistema de controle em cascata.
Esse sistema apresenta ótimos resultados para processos lentos e com alto número de distúrbios e por isso é considerado uma das melhores estratégias de controle que existe. O gráfico abaixo mostra uma comparação para o controle de temperatura de um mesmo processo usando o controle feedback e o controle cascata.
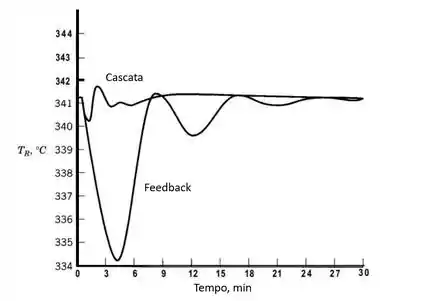
Controle cascata
Vamos começar a entender então como esse controle funciona.
O controle cascata pode ser explicado como dois controles feedback acoplados. No controle cascata temos dois sensores, dois controladores, porém apenas uma válvula.
Além disso, o controle cascata pode ser dividido em duas malhas, a malha primária (externa) e a malha secundária (interna):
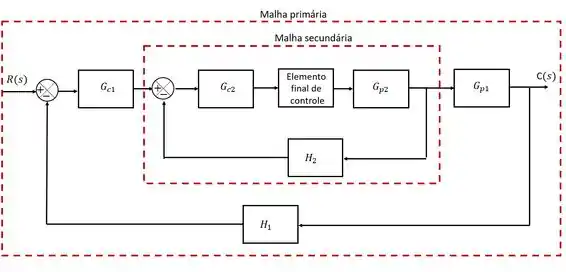
A malha primária é quem mede e controla a variável controlada do processo. Para a malha primária é como se a malha secundária fosse uma parte do processo. Repare que se toda a malha secundária for reduzida a apenas um bloco, esse bloco funcionaria como o elemento final de controle da malha primária que seria um feedback clássico.
A malha secundária mede e controla uma variável secundária que afeta diretamente a variável primária. Essa variável secundária tem, obrigatoriamente, dinâmica mais rápida e por isso ela é controlada primeiro de forma a corrigir o desvio da variável controlada o mais rápido possível. Alguns livros sugerem que a constante de tempo de seja pelo menos três vezes menor que a de .
Uma outra coisa bacana de se reparar é que o sinal de saída do controlador primário é quem determina o setpoint do controlador secundário. Na prática isso quer dizer que quando acontece algum distúrbio na variável primária, que é a nossa variável controlada, o controlador primário muda o setpoint da variável secundária fazendo ela se ajustar e corrigir o distúrbio da variável primária.
É por isso que em alguns livros a variável primária é chamada de mestre e a secundária é chamada de servo.

Como a variável secundária é a serva, ela é a primeira a corrigir algum distúrbio que aconteça no processo, isso pode ser notado pelo fato do elemento final de controle (válvula, bomba, amplificador, etc) estar diretamente ligado ao controlador secundário.
Por isso, uma exigência do controle cascata é que a malha secundária tenha resposta mais rápida às alterações na variável manipulada do que a malha primária. Caso isso não ocorra, o controle cascata fica instável.
Exemplo - controle cascata
Vamos ver um exemplo na prática de controle cascata comparando com um feedback.
Imagina que em um reator acontece uma reação exotérmica e deseja-se controlar a temperatura de saída desse reator. O controle pode ser feito através do feedback medindo-se a temperatura de saída e manipulando a entrada do reagente B no reator que é o reagente limitante, conforme a figura abaixo:
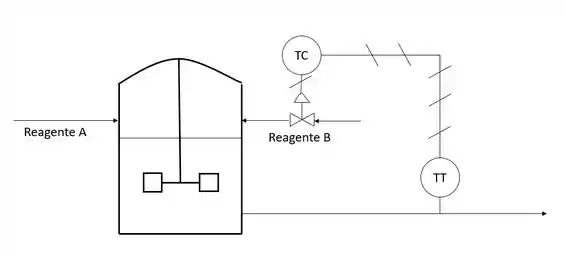
Vamos tentar pensar então em uma forma de introduzir o controle cascata no processo acima.
Recapitulando: precisamos controlar a temperatura de saída e estamos controlando a entrada do reagente limitante da reação exotérmica que está acontecendo no nosso reator.
Para introduzir o controle cascata, precisamos de uma variável secundária. A variável secundária é uma variável intermediária, isso porque ela “se encontra” sempre entre a variável manipulada e a controlada. Nesse caso, então, podemos adotar como variável secundária a temperatura dentro do reator.
Nesse cenário, nosso controle cascata ficaria assim:
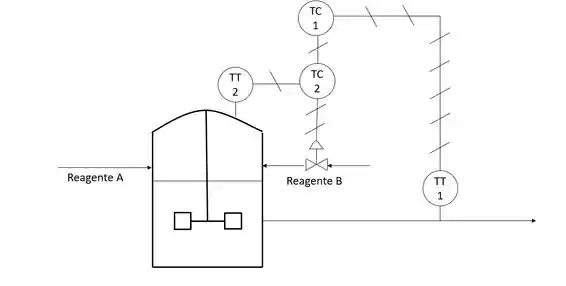
Dessa forma, quando varrições na temperatura do reator começarem a acontecer, a variável manipulada já será corrigida.
Repare também que a saída do controlador primário é o controlador secundário, pois como a gente viu ali em cima é o controlador primário quem determina o setpoint do controlador secundário.