Análise em frequência
Produzido por Alexandre NunesTeoria
Introdução
Uma técnica muito antiga e clássica de análise de sistemas de controle é a análise da resposta em frequência.
Essa técnica vai analisar o impacto da frequência quando temos entradas senoidais nos sistemas. Entradas senoidais gerarão respostas senoidais com a mesma frequência, porém com ângulo de fase e amplitude diferentes.
Por exemplo, considere um sistema com função de transferência de primeira ordem:
Vamos considerar que a entrada é uma entrada senoidal do tipo:
Onde:
amplitude;
frequência.
A transformada de Laplace dessa função é então:
Nós vimos como fazer isso no tópico de transformadas de Laplace, caso você não se lembre, dá uma revisadinha lá.
Sendo assim, a expressão para fica:
Cuja inversa é:
E, portanto, a saída também será do tipo senoidal, porém com alguns parâmetros diferentes.
As técnicas de análise em frequência são úteis então para analisar como esses parâmetros, principalmente ângulo de fase e amplitude variam de acordo com a frequência de entrada.
Então nesse tópico vamos entender primeiramente o que são esses conceitos e em seguida ver como eles são impactados pela frequência de entrada.
Definições
Suponha que a função de entrada seja da seguinte forma:
Então para esse caso a amplitude, , será e a frequência da entrada, , será .
O gráfico para essa entrada será então:
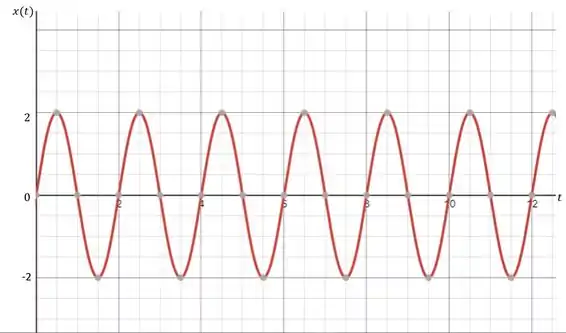
Agora suponha que essa entrada gere uma saída do tipo
Repare que a frequência da saída é igual a frequência da entrada, e sempre será assim. Entretanto a magnitude da saída é diferente, e além disso, temos um termo novo, , que é o que chamamos de ângulo de fase.
O gráfico para essa saída fica:
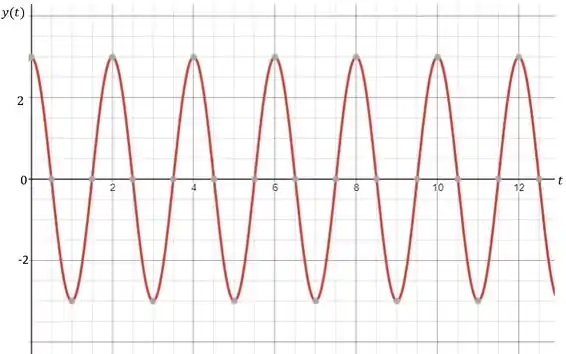
Então vamos às definições que serão importantes para nós:
Razão de amplitude () será a razão entre a amplitude da saída e a amplitude da entrada, ou seja:
Em alguns casos, podemos encontrar também a razão de magnitude () que nada mais é que a razão de amplitude dividida pelo ganho do processo:
E por fim temos também o ângulo de fase () que é o ângulo em radianos que avança ou atrasa a resposta com relação a entrada. No exemplo anterior por exemplo esse ângulo era e como ele era positivo nós dizemos que a resposta estava avançada em radianos com relação à entrada. Casso fosse negativo, seria um ângulo de atraso.
Razão de amplitude e razão de magnitude
Como vimos no início desse tópico, o objetivo da análise de frequência é analisar como a razão de amplitude e o ângulo de fase da resposta variam de acordo com a frequência da função da entrada.
Existem mecanismos matemáticos que nos permitem calcular esses parâmetros usando apenas os parâmetros da função de transferência do processo e a frequência da entrada.
Vamos sempre considerar como exemplo a função de transferência de primeira ordem padrão:
Para o cálculo da razão de amplitude nós vamos precisar calcular o módulo da função de transferência quando tende a :
O módulo de um quociente é o mesmo que o módulo do numerador pelo módulo do denominador:
Supondo positivo, o módulo de será o próprio e o módulo de um número complexo é a raiz quadrada da parte imaginária ao quadrado mais a parte real ao quadrado, ou seja:
E a razão de magnitude:
Sendo assim, quando tivermos uma função de transferência e desejarmos calcular sua razão de amplitude em função da frequência de entrada, devemos substituir por e calcular o módulo da função de transferência. Lembrando sempre que o módulo do quociente pode ser calculado pela divisão entre o módulo do numerador pelo módulo do denominador e que o módulo de um número complexo pode ser calculado da seguinte forma:
Ângulo de fase
O ângulo de fase também tem uma forma bem direta de ser calculado, ele será igual ao ângulo de fase da função de transferência quando tende a
Para o exemplo de função de primeira ordem:
O ângulo de fase de um quociente pode ser reescrito como o ângulo de fase do numerador menos o ângulo de fase do denominador:
O ângulo de fase pode ser algebricamente calculado como a da parte imaginária de um número:
Sendo assim para o nosso exemplo:
Resumindo tudo: para calcular o ângulo de fase da resposta em função da frequência de entrada a partir da função de transferência do processo devemos primeiramente substituir por e calcular o ângulo de fase da função de transferência. O ângulo de fase pode ser calculado fazendo-se o ângulo de fase do numerador menos o ângulo de fase do denominador. Se um número for puramente real seu ângulo de fase sempre será .
Partiu exercício?
Definições
Razão de amplitude e razão de magnitude
Ângulo de fase
Exercícios Resolvidos
Exercício Resolvido #1
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 10.1. Adaptado.
Determine a expressão analítica da magnitude da resposta em frequência e da fase da resposta em frequência para o sistema:
Passo 1
Para calcular a razão de amplitude e ângulo de fase da função de transferência, devemos sempre substituir por , sendo a frequência em da entrada. Sendo assim:
Passo 2
A razão de amplitude , pode ser calculada como o módulo da função de transferência:
O módulo de um quociente pode ser reescrito como o módulo do numerador dividido pelo módulo do denominador. Sendo assim:
O módulo de um número imaginário é a raiz quadrada do quadrado da parte imaginária mais o quadrado da parte real. Portanto:
Passo 3
O ângulo de fase de um quociente pode ser resscrito como a diferença entre o ângulo de fase dos dois termos. Sendo assim:
Para calcular o ângulo de fase de um número deve-se calcular o arcotangente da parte imaginária dividida pela parte real. Sendo assim:
Portanto:
Resposta
Exercício Resolvido #2
Elaboração própria
Determine a resposta analítica para a razão de amplitude e ângulo de fase da função de transferência abaixo:
Passo 1
Para calcular a razão de amplitude e ângulo de fase da função de transferência, devemos sempre substituir por , sendo a frequência em da entrada. Sendo assim:
Passo 2
A razão de amplitude , pode ser calculada como o módulo da função de transferência:
O módulo de um quociente pode ser reescrito como o módulo do numerador dividido pelo módulo do denominador. Sendo assim:
O módulo de um número imaginário é a raiz quadrada do quadrado da parte imaginária mais o quadrado da parte real. Portanto:
Passo 3
O ângulo de fase de um quociente pode ser resscrito como a diferença entre o ângulo de fase dos dois termos. Sendo assim:
Para calcular o ângulo de fase de um número deve-se calcular o arcotangente da parte imaginária dividida pela parte real. Sendo assim:
Portanto:
Resposta
Exercício Resolvido #3
Elaboração própria
Calule a razão de amplitude e o ângulo de fase para a resposta considerando a função de transferência abaixo:
A entrada é senoidal e tem a seguinte forma:
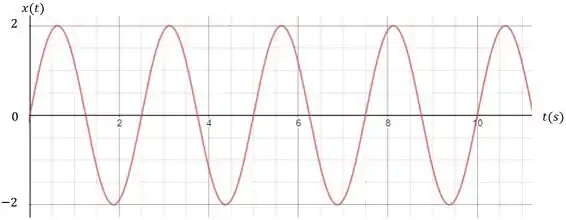
Dê a expressão da resposta .
Passo 1
Para calcular a razão de amplitude e ângulo de fase da função de transferência, devemos sempre substituir por , sendo a frequência em da entrada. Sendo assim:
Pelo gráfico podemos ver que a entrada efetua um ciclo a cada , sendo assim, a frequência em hertz será:
Para passar para :
Substituindo na função de transferência:
Passo 2
A razão de amplitude , pode ser calculada como o módulo da função de transferência:
O módulo de um quociente pode ser reescrito como o módulo do numerador dividido pelo módulo do denominador. Sendo assim:
O módulo de um número imaginário é a raiz quadrada do quadrado da parte imaginária mais o quadrado da parte real. Portanto:
Passo 3
O ângulo de fase de um quociente pode ser reescrito como a diferença entre o ângulo de fase dos dois termos. Sendo assim:
Para calcular o ângulo de fase de um número deve-se calcular o arcotangente da parte imaginária dividida pela parte real. Sendo assim:
Portanto:
Passo 4
A resposta terá a seguinte forma:
A frequência, , será a mesma da frequência da entrada, então:
O ângulo de fase já foi calculado:
Já para calcular a amplitude, devemos usar a definição de razão de amplitude, que é a razão entra a amplitude da saída pela amplitude de entrada
A razão de amplitude já foi calculada e a amplitude da entrada pode ser obtida pelo gráfico, sendo assim:
A expressão da resposta será, então:
Resposta
Exercício Resolvido #4
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 10.1. Adaptado.
Determine as expressões analíticas para a magnitude e a fase da resposta de:
Passo 1
Primeiramente vamos efetuar a multiplicação entre os termos do denominador:
Para calcular a razão de amplitude e ângulo de fase da função de transferência, devemos sempre substituir por , sendo a frequência em da entrada. Sendo assim:
Como:
Teremos:
Passo 2
A razão de amplitude , pode ser calculada como o módulo da função de transferência:
O módulo de um quociente pode ser reescrito como o módulo do numerador dividido pelo módulo do denominador. Sendo assim:
O módulo de um número imaginário é a raiz quadrada do quadrado da parte imaginária mais o quadrado da parte real. Portanto:
Passo 3
O ângulo de fase de um quociente pode ser escrito como a diferença entre o ângulo de fase dos dois termos. Sendo assim:
Para calcular o ângulo de fase de um número deve-se calcular o arcotangente da parte imaginária dividida pela parte real. Sendo assim:
Portanto:
Resposta
Exercício Resolvido #5
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 263, Exemplo 8-4.4
Determine as expressões de e para um integrador:
Passo 1
Primeiramente devemos expressar nossa função de transferência substituindo por .
Passo 2
A razão de amplitude pode ser calculada através do módulo da função de transferência:
Como:
O módulo de um número imaginário é a raiz quadrada do quadrado da parte imaginária mais o quadrado da parte real. Nesse caso, o numerador é um número real puro e o denominador é um imaginário puro. Portanto:
Passo 3
O ângulo de fase de um quociente pode ser escrito como a diferença entre o ângulo de fase dos dois termos. Sendo assim:
Para calcular o ângulo de fase de um número deve-se calcular o arcotangente da parte imaginária dividida pela parte real. Sendo assim:
Portanto:
Uma coisa bacana de lembrar é que o ânglo de fase de um número real puro sempre será e de um número imaginário puro sempre será
Resposta
Exercício Resolvido #6
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 262, Exemplo 8-4.2
Considere a seguinte função de transferência de avanço de primeira ordem:
Esta é uma função de transferência composta de um ganho vezes um avanço de primeira ordem. Determine as expressões para e .
Passo 1
O primeiro passo será reescrever a função de transferência em termos de :
Passo 2
A razão de amplitude pode ser calculada através do módulo da função de transferência:
Como:
O módulo de um número imaginário é a raiz quadrada do quadrado da parte imaginária mais o quadrado da parte real. Portanto:
Passo 3
O ângulo de fase de um produto pode ser resscrito como a soma do ângulo de fase das parcelas:
Para calcular o ângulo de fase de um número deve-se calcular o arcotangente da parte imaginária dividida pela parte real. Sendo assim:
Portanto:
Repare que o ângulo de fase é positivo, é por isso que esse tipo de função de transferência do exercício é chamada de função de transferência de avanço.
Resposta
Exercício Resolvido #7
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 262, Exemplo 8-4.1
Considere a seguinte função de transferência de segunda ordem:
Determine as expressões para e .
Passo 1
Primeiramente devemos substituir por
Como:
Passo 2
A razão de amplitude pode ser calculada através do módulo da função de transferência:
Como:
O módulo de um número imaginário é a raiz quadrada do quadrado da parte imaginária mais o quadrado da parte real.
A parte real do número do denominador é e a parte imaginária é . Sendo assim:
Passo 3
O ângulo de fase de um quociente pode ser escrito como a diferença do ângulo de fase dos termos:
Para calcular o ângulo de fase de um número deve-se calcular o arcotangente da parte imaginária dividida pela parte real. Sendo assim:
Portanto:
Resposta
Exercício Resolvido #8
Elaboração prórpria
Determine expressões analíticas para a magnitude e a fase da resposta de:
Passo 1
Primeiramente vamos efetuar a multiplicação entre os termos do denominador:
Para calcular a razão de amplitude e ângulo de fase da função de transferência, devemos sempre substituir por , sendo a frequência em da entrada. Sendo assim:
Como:
Teremos:
Passo 2
A razão de amplitude , pode ser calculada como o módulo da função de transferência:
O módulo de um quociente pode ser resscrito como o módulo do numerador dividido pelo módulo do denominador. Sendo assim:
E o módulo de um produto é igual ao produto dos módulos:
O módulo de um número imaginário é a raiz quadrada do quadrado da parte imaginária mais o quadrado da parte real. Portanto:
Ou ainda:
Passo 3
O ângulo de fase de um quociente pode ser escrito como a diferença entre o ângulo de fase dos dois termos. Sendo assim:
E o ângulo de fase de um produto pode ser dividido como a soma do ângulo de fase das parcelas:
Para calcular o ângulo de fase de um número deve-se calcular o arcotangente da parte imaginária dividida pela parte real. Sendo assim:
Portanto: